复杂混联体系失效区域的确定与积分方法比较

蒋友宝，廖 强，张建仁

(长沙理工大学 土木与建筑学院，湖南 长沙410114)

其中，Ai为求积系数，与函数f(y)无关。

若积分区间是［a，b］，可通过变量置换

0 引 言

积分方法是求解结构可靠度的主要方法之一。对于简单的失效方程，各种积分方法一般均能够给出较为精确的可靠度计算结果。但实际工程结构一般具有多个失效模式、多维随机变量［1-3］，因而其体系失效边界将为一复杂(分段、多维非线性)函数。在这种情形下，如何计算其可靠度，引起了较多研究者的关注。

Pandey 等［4］依据条件概率理论提出了一种计算体系可靠度的PCM(Product of Conditional Marginal)方法，将多维积分转换为一系列条件边缘分布概率的乘积，克服了多维情形下直接积分工作量较大的不足。随后，Yuan 和Pandey［5］、Nadarajah［6］分析了PCM 法在系统可靠度计算中存在的不足并进行了改进。涂茂红等［7］通过修正PCM 方法计算过程中的相关系数矩阵，得到了一种改进的G-PCM 方法(General PCM)，但其迭代算法较为复杂，且对其用于复杂混联体系可靠度计算的适用性没有说明。

当结构体系失效边界为一复杂函数时，直接积分方法因无任何简化假设，因此其计算精度在理论上要较各种PCM 方法及其改进方法要高，但其用于体系可靠度分析的难点是计算量较大。针对此不足，贡金鑫等［8］提出了一种基于Gauss-Hermite 积分的可靠度积分计算方法。该方法利用Gauss-Hermite 积分快速收敛的特性，使计算效率成倍提高。但应指出的是，Gauss-Hermite 积分对积分0 点的依赖性过强;当失效边界为复杂曲面时，如对失效概率有重要贡献的区域有多个且较为分散时，其积分0 点将很难选取，而一旦选取不当则其计算精度会变得较差。

Zhao 等［9］提出了一种基于降维分解的DRI(Dimension Reduction Integration)方法，该方法使用降维分解技术将串联结构体系失效函数表达为多个低维函数的和;然后采用Gauss-Hermite 积分得到多个低维函数的前4 阶矩，并用此4 阶矩来求得体系可靠度。其优点是不必考虑各失效模式的相关系数矩阵，但当各失效模式方程形式改变时，该方法的计算结果会波动。由可靠度基本理论知，只有对失效曲面进行相应分析方才会克服此不足。为此，蒋友宝等［10］对串联结构体系失效方程边界的复杂特性进行了分析，并建议了一种基于梯形积分和降维分解的体系可靠度计算方法，数值分析表明该方法具有较好的精度与效率。

另外，作为积分方法之一的Monte-Carlo 方法由于不需要考虑失效边界的复杂特性和随机变量的相关系数矩阵，能对结构的可靠度直接进行计算，因而常作为校核其他可靠度计算方法的手段。但对于高可靠性问题，Monte-Carlo 方法需要巨大的样本数量，往往难以接受。为了提高计算精度和效率，研究者提出了多种重要抽样法［11-14］。但这些方法由于其固定的随机性，即使采用重要抽样方法也无法消除计算结果随样本数量的随机波动性，且复杂混联体系的重要抽样密度函数一般较难确定。

可见，研究合适的积分方法来提高复杂混联体系可靠度积分计算的精度与效率仍具有较大的价值。为此，本文研究了复杂混联体系可靠度计算中积分区域的快速确定方法，并对比了复杂失效方程下常用的梯形积分、Gauss-Hermite 积分和Gauss-Legendre 积分的计算精度与效率。

1 积分区域的快速确定方法

1.1 混联失效模式下积分区域的复杂性

由于Rosenblatt 变换可将非正态随机变量转化为标准正态分布变量，因此不失一般性，可假定各随机变量均服从标准正态分布。根据定义，结构的失效概率pf可计算为

其中，X={x1，x2，…，xn}，为各随机变量组成的联合向量;φ(X)为多维标准正态联合分布的概率密度函数;Ω 为失效域。

而结构可靠指标β 与失效概率之间的换算式为

在标准正态空间中，结构体系各失效模式对应的曲面方程一般为非线性的，但对实际工程结构的初步研究［15-16］表明，这种非线性程度一般较弱，因而可用FORM 方法来计算其可靠度，即采用验算点处的切线平面来代替非线性失效曲面。

当结构体系各失效曲面用切线平面近似后，设可得到m 个线性失效模式，分别记为g1，g2，…，gm，而D1，D2，…，Dm为各线性失效模式的验算点。对于多个线性的超平面集合，失效域Ω 一般可表示为下列点的集合

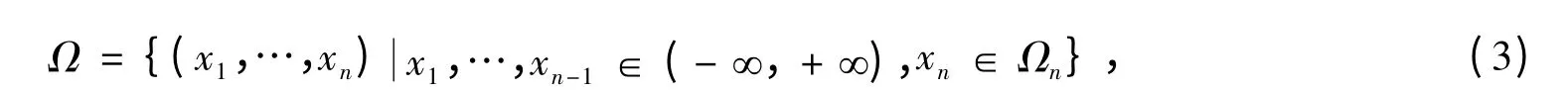
其中，Ωn区域需由体系失效边界确定，因此式(1)转变为

其中，u(x1，…，xn-1)表示当x1，x2，…，xn-1给定时xn变量在失效域Ωn内的积分值，可计算为

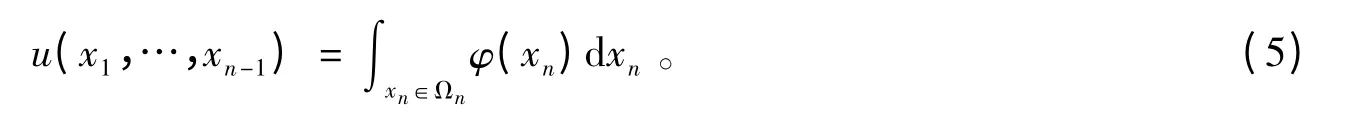
当失效模式数量较少时，失效域Ωn一般较简单，可容易确定。例如，在图1 中，失效模式g3和g4为并联组成，其余为串联组成。可见，当x1变量取图中定值且沿x2轴方向搜寻与体系失效边界的交点时，可能的交点数量有4 个，但直观判定实际的交点只有P1和P2，对应的Ωn为［-∞，x2P1］和［x2P2，+∞］。而当变量维数和失效模式数量增多时，由于不能直观显示且可能的交点数量更多，因此xn对应的积分区域Ωn较为复杂，此时需结合数值计算手段方能确定其积分区域。

1.2 积分区域的快速确定

不失一般性，考虑如下一典型混联体系，其组成方式见图2，共有r 个串联失效模式集合，各串联集合中分别包括s1，s2，…，sr个并联的失效模式。

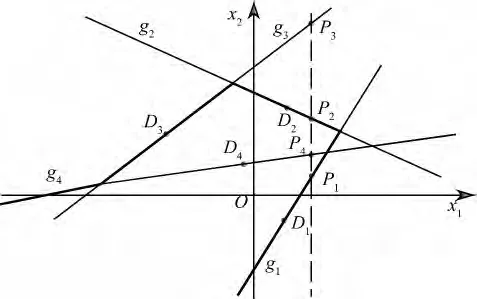
图1 结构混联体系的积分区域Fig.1 Domains for integral calculation for a structural compound system

图2 典型混联体系组成Fig.2 Components of a typical compound system

如前所述，设总的失效模式数量为m，显然有

根据每个失效模式方程确定出沿xn方向直线与失效边界的m 个可能点。然后按照上述组成方式确定出位于边界上的真实点。例如对于jth串联模式，它是由sj个并联失效模式组成，对应的可能点为Pj，1，Pj，2，…，Pj，sj。若其中之一的Pj，i在失效边界上，则其必然满足

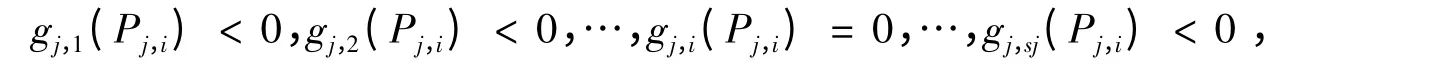
即该点在自身失效模式对应的边界(极限状态曲面)上，而在其他失效模式对应的失效域内。

为阐述方便，记在边界上的Pj，i为Pj，ij。对r 个串联失效模式进行同样运算，可得到对应的可能点为P1，i1，P2，i2，…，Pr，ir。若其中之一的Pj，ij在失效边界上，则其必然满足

即该点在自身失效模式对应的边界(极限状态曲面)上，而在其他失效模式对应的安全域内。

根据得到的失效边界上的若干个点，将xn变量划分成多个区间，可确定出相应的积分区域Ωn，进而采用式(4)和式(5)完成积分计算。

2 复杂失效边界下各种积分算法的适用性分析

2.1 梯形求积公式

梯形求积公式是指在给定区间［a，b］内构造被积分函数f(y)的线性插值多项式，从而得到的积分计算式。其积分计算式为

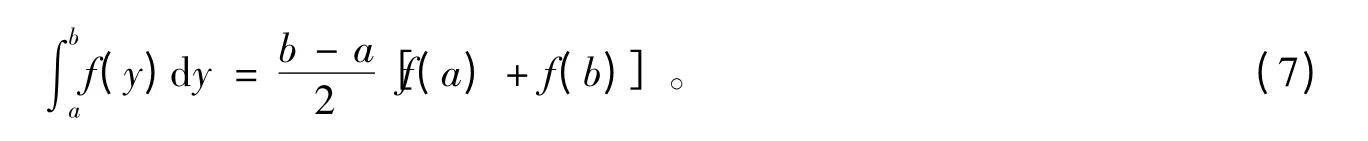
2.2 Gauss 型求积公式

Gauss 型求积公式是指在给定区间［a，b］内取多个互异的求积节点来构造被积分函数f(y)的插值多项式，从而得到的积分计算式。常用的积分计算式有Gauss-Legendre 型求积公式和Gauss-Hermite 求积公式两种。

2.2.1 Gauss-Legendre 型求积公式

当给定权函数ρ(y)=1 和积分区间［-1，1］，Gauss-Legendre 型求积公式为

其中，Ai为求积系数，与函数f(y)无关。

若积分区间是［a，b］，可通过变量置换

将积分区间［a，b］变为积分区间是［1，-1］，此时积分式转化为

2.2.2 Gauss-Hermite 型求积公式

当给定权函数ρ(y)=e-y2，积分区间为(-∞，∞)时，Gauss-Hermite 求积公式为

当应用式(11)来计算式(4)中的失效概率时，需做一定的函数变换。对于多维标准正态联合分布，其概率密度函数为

作变量置换

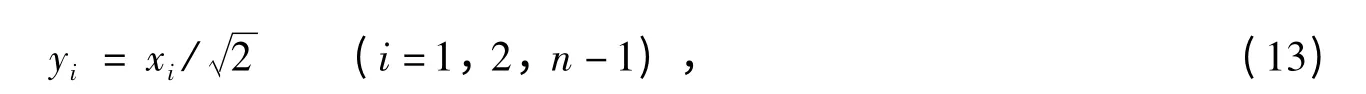
因此，在Y 空间中，失效概率计算式(4)变为

其中，u'(y1，…，yn-1)为变量置换后与u(x1，…，xn-1)对应的函数。

式(14)即可采用Gauss-Hermite 积分式进行计算。

2.3 各种积分方法的适用性分析

对于Gauss-Legendre 和Gauss-Hermite 型求积公式，其求积节点yi和求积系数Ai见表1。可知，Gauss-Legendre 积分和Gauss-Hermite 积分均是采用固定的积分节点位置和对应的求积系数来计算失效概率的。当体系失效边界较为复杂时，重要积分区域(对失效概率有重要贡献的积分区域)将较为复杂。此时，即使增加积分节点的数量，但由于Gauss-Legendre 积分或Gauss-Hermite 积分节点之间位置的相对固定性和积分节点间距的不均衡性(有些节点间距大，有些节点间距小)，因此在较坏的情形下，这些积分节点与反映重要积分区域复杂性的特征点(位于失效边界上的验算点等)会有较大偏差，致使其计算精度变得较差。

表1 Gauss-Hermite 与Gauss-Legendre 积分节点和积分系数Tab.1 Nodes and weight factors for Gauss-Hermite and Gauss-Legendre integration

而梯形积分节点是等间距的，即为均匀分布，通过增加积分节点的数量，可同步缩小各积分节点之间的间距，同时各积分节点与反映重要积分区域复杂性的特征点之间的偏差亦会稳步地减小，即能较好地与重要积分区域相匹配，因而在这种情形下将具有较好的适用性。

3 算例分析

3.1 算例1

考虑一验算点较为分散且具有2 个失效模式的串联系统，2 个失效模式为

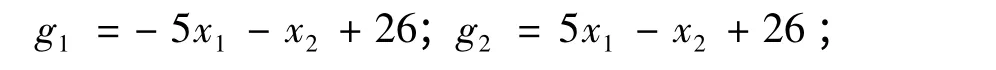
其中，x1，x2服从标准正态分布。

对于此算例，可求得两个验算点为:D1(5，1)和D2(-5，1)，其对应的重要积分区域已大为超出7节点Gauss-Hermite 积分对应的区间［-3.7505，3.7505］，因此若在Y 空间中不进行坐标旋转(Case 1)，则其积分节点将很难反映出此重要积分区域的特性，计算精度将较差;反之若在Y 空间中进行坐标旋转，即将y'2轴指向y1轴，则其积分节点将能较好地反映出此重要积分区域的特性，计算精度又将会变得较好。

由于积分区间、积分节点数量的不同会对Gauss-Legendre 积分和梯形积分节点的位置产生较大的影响，因而为研究其影响规律，此处两种积分方法各考虑三种情形，其中14 个节点的Gauss-Legendre 积分结果是指将积分区间［-6.0，6.0］划分成［-6.0，0］和［0，6.0］两个子区间，然后在每个子区间上均采用7 个节点的Gauss-Legendre 积分式进行计算。不同情形下积分节点与被积分函数见图3。

图3 算例1 积分函数与各积分方法的节点分布Fig.3 Illustration of the integral function and integral nodes of each method for example 1

可见，此算例的被积分函数仅在两个点(x1=±5.13)附近取值很大，而其他区域取值极小，因此只有当积分节点能落在这两个点(x1=±5.13)附近时，积分函数的复杂性才能被反映出来，对应的积分方法才具有较好的精度。而如前所述，由于Gauss-Legendre 积分节点之间位置的相对固定性和积分节点间距的不均衡性，使得其计算结果较不稳定，在不利情形下(积分区间为［-6.0，6.0］，7 个节点)其积分节点偏离x1=±5.13 较多，计算结果将变得较差。具体各种方法的计算结果见表2。

表2 算例1 计算结果Tab.2 Calculated results for example 1

若以Monte Carlo 方法为精确解，可见各种情形下梯形积分方法具有较好的稳定性，而Gauss-Legendre 积分方法的稳定性较差。例如，同样采用17 个积分节点，当积分区间由［-5.5，5.5］扩大为［-6.0，6.0］时，梯形积分计算结果变化不大，均较为精确;而同样采用7 个Gauss-Legendre 积分节点，当积分区间为［-5.5，5.5］时其计算结果较为精确，而一旦积分区间稍有改变，如扩大为［-6.0，6.0］时，其计算结果就会变得较差，此时β 相差6.45%，进一步按式(2)计算知对应的pf相差约5 倍。

这表明，在Gauss-Legendre 积分节点数量一定时，若积分区间选择不合理，则其积分计算精度将会较差;当可接受较多计算量时，选用梯形积分来计算可靠度会是一个较好的选择，因为其积分节点是等间距的，确定较简单，且其计算结果较为稳定。

3.2 算例2

某体系的失效方程如下所示:

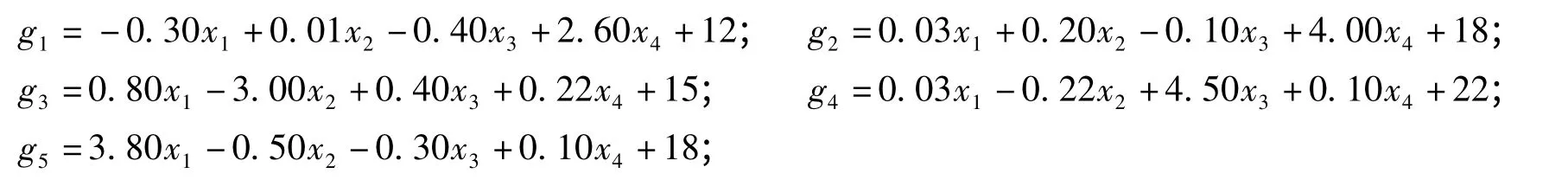
其中:g1与g3为并联体系，g2与g4为并联体系;x1、x2、x3和x4均服从标准正态分布。

依据文中提出的失效域确定方法，得到的各验算点与失效边界的几何关系见表3。

表3 算例2 各失效模式验算点Tab.3 Checking points of all failure modes for example 2

可知，仅失效模式g5对应的验算点在失效边界上，且在Y 空间中此算例的重要积分区域与7 节点Gauss-Hermite 积分区间组成的超立方体吻合较差，因而若不进行合理的坐标旋转将得到较差的计算结果(Case 1);若将坐标系合理旋转，即Y'4轴指向各失效模式的中心点，则能得到较好的计算结果(Case 2)。具体不同积分方法计算得到的可靠指标见表4。

若以Monte Carlo 方法为精确解，可见Gauss-Legendre 积分方法的计算精度依然较不稳定，与积分区间、积分节点数量的选取有很大关联:选取不当时其计算误差会很大，如将积分节点数量增加至14 时，积分计算结果反而变得较差［β 相差5.40%，进一步按式(2)计算知对应的pf相差约3 倍］;而选取合理时误差则较小。而梯形积分方法的计算精度在各种情形下均较为稳定，因而当可接受较多计算量时是计算可靠度的一个较好选择。

表4 算例2 计算结果Tab.4 Calculating results for example 2

3.3 算例分析讨论

上述算例分析表明，无论其为串联体系还是复杂混联体系，文中提出的基于体系组成方式的失效域确定方法均较为有效，可为积分计算提供较好的基础。

当体系失效边界较为复杂时，Gauss-Hermite 积分方法与Gauss-Legendre 积分方法的计算结果较不稳定，为获得较高的计算精度，需进行合理的坐标旋转或积分区间确定;而在复杂体系失效边界的情形下这往往较难实现。

梯形积分方法仅需通过简单地增加积分节点数量便能较好地匹配复杂的重要积分区域，计算结果较为精确且稳定，具有较好的适用性。若能接受较多计算量时，该方法可作为一种推荐方法来计算结构体系可靠度。

4 结 论

本文考虑失效模式的组成方式，提出了一种实用的复杂混联体系失效区域的确定方法，并结合算例分析对比了不同积分算法的计算精度与效率。分析得到如下结论:

①对于复杂混联体系，可依据其混联组成方式较精确地确定出当其余维变量取定值时对应的条件失效区间，进而得到其体系失效区域。算例分析表明该思路能达到较好效果;

②当体系失效边界较为复杂时，采用等间距积分节点的梯形积分方法通过增加积分节点数量，可同步缩小各积分节点之间的间距，因而各积分节点与反映重要积分区域复杂性的特征点之间的偏差会稳步地减小，具有较好的适用性;

③Gauss-Hermite 和Gauss-Legendre 积分方法的计算精度较不稳定，其与选取的积分坐标系和积分区间有关，若积分坐标系和积分区间选取不合理，会导致其积分节点不能较好地匹配复杂的重要积分区域，此时其计算精度将会较差。

［1］ KIM D S，OK S Y，SONG J，et al.System reliability analysis using dominant failure modes identified by selective searching technique［J］.Reliability Engineering＆System Safety，2013，119:316-331.

［2］ LEE Y J，SONG J.Finite-element-based system reliability analysis of fatigue-induced sequential failures［J］.Reliability Engineering＆System Safety，2012，108:131-141.

［3］ 秦荣，梁汉吉，孙千伟.大型复杂结构体系可靠度分析的QR 法［J］.广西大学学报:自然科学版，2008，33(1):10-15.

［4］ PANDEY M D，SARKAR A.Comparsion of a simple approximation for multinormal integration with importance samplingbased simulation method［J］.Probabilistic Engineering Mechanics，2002，17:215-218.

［5］ YUAN X X，PANDEY M D.Analysis of approximations for multinormal integration in system reliability computation［J］.Structural Safety，2006，28(4):361-377.

［6］ NADARAJAH S.On the approximations for multinormal integration［J］.Computers＆Industrial Engineering，2008，54(3):705-708.

［7］ 涂宏茂，钱云鹏，姬广振，等.改进的结构系统可靠度的条件边缘乘积法［J］.工程力学，2012，29(10):321-326.

［8］ 贡金鑫，陈晓宝，赵国藩.结构可靠度计算的Gauss-Hermite 积分方法［J］.上海交通大学学报，2002，36(11):1625-1629.

［9］ ZHAO Y G，LIN Y S，ANG A H S.Dimension reduction integration for system reliability［C］//KATAFYGIOTIS L S，ZHANG L，TANG W H，et al.Proceedings of the Asian-Pacific Symposium on Structural Reliability and its Applications.Hong Kong:The Hong Kong University of Science and Technology，2008:310-315.

［10］蒋友宝，刘扬，张建仁.基于失效边界特性的体系可靠度计算方法［J］.工程力学，2010，27(8):77-82.

［11］金伟良.结构可靠度数值模拟的新方法［J］.建筑结构学报，1996，17(3):63-72.

［12］MORI Y，KATO T.Multinormal integrals by importance sampling for series system reliability［J］.Structural Safety，2003，25:363-378.

［13］ZHANG F，LU Z Z，CUI L J，et al.Reliability sensitivity algorithm based on stratified importance sampling method for multiple failure modes systems［J］.Chinese Journal of Aeronautics，2010，23(6):660-669.

［14］PATELLI E，PRADLWARTER H J，SCHUËLLER G I.On multinormal integrals by importance sampling for parallel system reliability［J］.Structural Safety，2011，33(1):1-7.

［15］KIM S H，NA S W.Response surface method using projected vector sampling points［J］.Structural Safety，1997，19(1):3-19.

［16］JIANG Y B，ZHANG J R.Characteristic analysis of load effect function under complex loads［C］// CHOI V C K.Proceedings of Advances in Structural Engineering and Mechanics.Jeju，Korea:John Wiley＆Sons，2008:3251-3260.