珠江三角洲城市空气质量的区域影响分析

滕 丽，卢 君

(广州大学 地理科学学院，广东 广州 510006)



珠江三角洲城市空气质量的区域影响分析

滕 丽，卢 君

(广州大学 地理科学学院，广东 广州 510006)

基于广东省环境信息综合发布平台发布的珠三角9城市空气质量日报数据构建VAR模型，通过格兰杰检验和脉冲响应分析，探讨2002～2012年珠三角9城市空气质量的区域影响特征。结果显示：珠三角9城市间空气质量的区域影响包括自我影响和跨域影响。且城市个体的自我影响是负效应，其强度远远超过跨域影响。在跨域影响中单向性影响占比84%，双向性影响占比16%，邻域影响占42%，非邻域影响占比58%。南部沿海城市影响范围普遍大于北部城市的影响范围。具有因果关系的城市间的跨域影响中，65%表现为正效应，22%为负效应，有13%显示为正负效应转换。而正负效应转换的情况说明存在两种不同的影响模式。

空气质量；API指数；跨域影响；向量自回归模型

0 引言

随着区域经济发展，资源环境问题对区域经济增长的限制性影响加剧。珠江三角洲是中国自然地理环境独特，人口经济高度密集的地区之一。区域资源开发强度大，发展速度快。人地之间相互作用剧烈，资源环境问题对该地区经济发展的限制性凸现。其中大气污染问题是珠三角面临的主要环境问题之一。而城市空气质量的区域影响是建立跨域生态补偿机制的重要基础，对区域环境治理政策制定具有重要意义。

城市空气质量的区域影响是大气污染物空间扩散的结果。在环境科学领域，对大气污染扩散的研究主要基于大气动力学理论，通常采用高斯模式及其变形模式，统计模式、大气压扩散相似模式或K模式等精确模拟污染物浓度的时空分布及其变化[1-3]。对珠三角地区的实证研究主要有余纬等采用数值模拟分析了珠三角一次重空气污染过程的特征[4]。胡晓宇等利用 Models-3/CMAQ 模拟系统，对珠江三角洲地区2006 年10 月的大气PM10 污染进行模拟研究。通过敏感性分析获得各城市PM10 浓度随不同污染源削减的变化情况，量化出城市间空气污染的相互影响，结果显示城市间输送已成为造成珠三角地区PM10 污染的重要因素[5]。王淑兰的数值模拟结果也显示珠三角城市之间大气污染物存在相互输送的关系，其中广州市大气污染最容易与周边城市发生相互作用[6]。这些研究为本文的研究结果提供了较好的对照和验证。作为珠三角空气质量相对较差的城市，广州空气质量问题也得到了较多讨论。如汤惠君分析了广州市1981～1997年的大气监测资料，指出广州大气污染物的时空分布特征与其气象条件、污染源的分布、排放强度的相关性较大[7]。沈佳芬等利用2001～2004年广州市空气自动监测点监测的PM10日平均浓度数据，分析了广州市PM10的时空变化特征。揭示了单一城市多种污染物的时空分布特征[8]。马民涛采用传统的空气污染负荷方法揭示广州市大气环境质量演变特征与经济发展的相关性[9]。这些研究揭示了在特定时间段广州市的大气污染分布状况，并对其形成原因提供了多角度的理解，但是单个城市的研究往往对外源影响因素考虑不够，所以有必要将城市置于区域的背景中去开展研究。

总之，数值模拟适合对短期内污染物空间扩散的微观机制做出解释，但是数值模拟一般将空间划分为若干个环境单元，环境单元与行政单元并非完全耦合，在应用到以行政单元界定的跨域环境管理决策时往往有一定的局限性[10，11]。在属地管理的权限约束下地方政府对跨域空气污染治理失效，有必要开展基于行政单元的空气质量的区域影响研究，为建立城市间的生态补偿机制和环境政策决策提供参考。本文基于VAR模型以珠三角9城市为空间单元，量化分析珠三角9城市2002～2012年间空气质量的区域影响特征。

1 模型原理

向量自回归(简称VAR)模型是一种不以经济理论为基础，而是把系统中的每一个内生变量作为系统中所有内生变量的滞后值的函数来构造模型，从而估计出全部内生变量的动态关系[12]。VAR模型是一种基于数据构建的统计学模型，将每个进入模型的变量都视为平等的。自西姆斯1980年将该模型引入经济学之后，模型常常用于预测相互联系的时间序列系统和分析随机扰动对变量系统的影响[13][14]。VAR(p)模型的基本形式是：

yt=φ1yt-1+…+φpyt-p+εtt=1，2…T

(1)

式中：yt是k维内生变量向量，p是滞后阶数，T是样本个数，εt是k维扰动列向量。

VAR模型除了能考察变量来自于自身的影响，还能考察来自于其他变量的影响。在理论上，一个城市的空气质量不仅与其前期空气质量有关，也可能受到其他城市空气质量的影响。所以将VAR模型运用于珠三角9城市的空气质量的区域影响研究是适合的。

运用VAR模型的方法策略(图1)首先针对珠三角城市空气质量，建立VAR模型，每个城市的空气质量都是一个序列，9个城市共有9个序列进入模型，最后得到9个方程。考虑到大气污染物的滞留时间有限，模型的滞后阶段设定为2。用最小二乘法运行VAR(2)模型并采用AR根图检验其稳定性，若稳定则代表珠三角城市间空气质量存在长期均衡关系。珠三角城市间空气质量的相互影响不是一种随机现象，而是具有统计规律的。其次基于VAR模型开展珠三角城市对的格兰杰因果检验。由于格兰杰因果关系判断具有序列平稳且具有协整性的要求，只有通过单位根检验和协整检验的城市对才进一步进行格兰杰因果关系检验。最后为了一步判断城市间空气质量相互影响强度。该方法策略说明了分析的逻辑过程是客观的。即只对满足一定条件的城市对进行空气质量相互影响判断。因为空气质量的区域影响是一种非常复杂的自然现象，在缺少大气动力机制基础的情况下，这样的方法策略可以防止对任意两个变量进行主观判断。

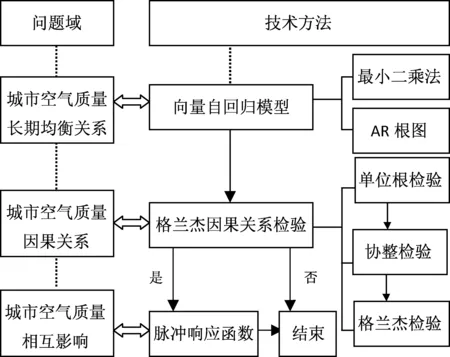
图1 方法策略

2 数据来源与处理

数据来源于2002～2012年广东省环境信息综合发布平台(www-app.gdepb.gov.cn)发布的珠江三角9大城市的空气污染指数日报数据。空气污染指数(Air Pollution Index，简称API)是将监测的几种空气污染物浓度简化成为单一的概念性指数值形式，并分级表征空气污染程度和空气质量状况的指标。直接使用空气污染指数来研究城市间空气质量的相互溢出关系具有不合理性，因为各污染物的扩散条件、介质和特征各不相同，基于空气污染指数的城市间相互溢出关系的分析难以从机制上深入解释。所以有必要将空气污染指数换算成首要污染物浓度。一方面将合成指标转换为单一指标，消除了机制解释的障碍，另一方面将单一指标替代合成指标所面临的可代表性问题降到最低。通过对珠三角个城市2002～2012年首要污染物，可吸入颗粒物(即PM10)的频数统计，在2002～2012年，珠三角9城市的PM10为首要污染物出现的频数均在80%以上，所以用PM10浓度来表征珠三角城市的空气质量较为合适(表1)。

表1 珠江三角洲各城市首要污染物为可吸入颗粒物的频数(2002～2012年)

因此通过下式将各城市2002～2012年的空气污染指数转换为PM10浓度。为了降低短时、随机影响因素的干扰，同时考虑PM10在空气中滞留或扩散的时间较长，所以用于VAR建模的PM10浓度指标采用了周平均浓度。

(1)

式中：I为污染物的污染指数，C为污染物的浓度，C大和C小分别为C所处的浓度段的上下值范围，I大和I小则为该浓度段对应的API值的上下限。

3 计算结果与分析

3.1 VAR模型回归结果

从VAR系统整体来看，依据AIC和SC信息量取值最小原则，模型阶数为2时，AIC值(-70.684)小于SC值(-66.714)，满足统计合理性。9个子方程的可决系数R2除了广州稍低(0.58)以外，其他均在0.84以上，说明各变量所形成的结构性相关较强(表2)。AR根图的结果显示所有根的模的倒数均位于单位圆内，模型是稳定的。珠江三角洲9城市的空间质量相互影响关系是长期稳定的(图2)。

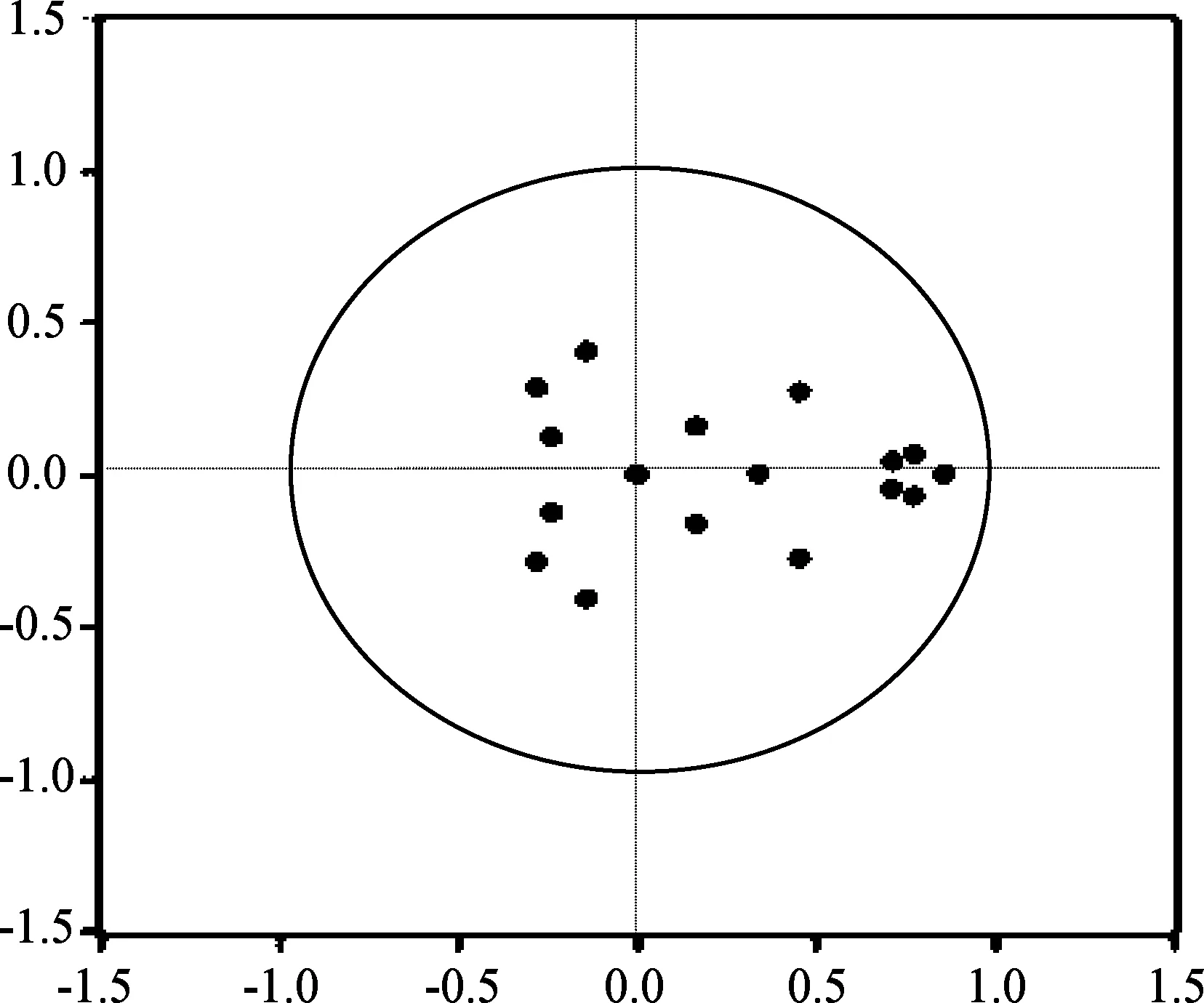
图2 珠三角9城市VAR模型的AR根图

结果城市广州东莞佛山惠州江门深圳珠海肇庆中山R20.6480.890.8890.870.9190.9090.8650.8740.921可调R20.5870.8720.8690.8470.9060.8930.8420.8520.907F10.64547.05746.18838.64266.11357.50237.07840.05967.562最大似然354.735476.061475.661468.087472.863484.502485.762462.955485.097AIC-5.15-7.016-7.01-6.894-6.967-7.146-7.166-6.815-7.155SC-4.709-6.575-6.569-6.452-6.526-6.705-6.724-6.374-6.714行列式残差协方差(dofadj.)4.57E-43行列式残差协方差1.02E-43最大似然4774.464AIC-70.684SC-66.714

3.2 格兰杰检验结果

格兰杰因果检验结果表明在珠三角各个城市间的空气质量的区域影响差异比较明显。空气质量具有双向因果关系的3对城市分别是广州-惠州，广州-深圳，深圳-惠州，占比16%。具有单向因果关系的17对城市占比84%。所以珠三角地区城市间空气质量以单向影响为主(表3)。

由于环境影响是市场失灵的，所以地方政府具有将一些有污染的产业布局到行政区边缘地带的倾向。接近行政边界附近的产业布局可能给邻近区域带来环境影响。所以从具有因果关系的城市间是否拥有公共地理边界的角度观察，珠三角各城市空气质量邻域影响的占42%，非邻域影响的占58%。

从影响范围的大小看，深圳市的空气质量影响范围最广，达到5个城市。其次是中山、珠海，其影响的城市分别为4和3个，其余城市的影响范围均在1～2个城市。所以珠三角地区PM10浓度值较高的广州、佛山和东莞空气质量的影响有限，而位于沿海的深圳、中山、珠海等城市的空气质量影响范围较广。之所以形成这样的格局，是因为珠三角大致是一个北高南低，开口在南的马蹄形地貌，南部城市的大气污染物会随着东南风或西南风向北扩散，而广佛莞北部受山地影响，污染物扩散条件较差，影响范围受限。

表3 空气质量具有格兰杰因果关系的城市

注：*城市A是城市B的格兰杰原因；[]中的数字为格兰杰因果检验的置信度P值；(Y)表示与城市A有公共边界；(N)表示与城市A没有公共边界.

3.3 脉冲响应结果

脉冲响应分析就是用来衡量来自随机扰动项的一个新息冲击对内生变量当前和未来值之间的动态交互作用及其效应。运用广义脉冲响应函数分析空气质量具有因果关系的城市之间的冲击响应，冲击响应期设定为20期。脉冲响应曲线图的纵坐标分别表示一个单位冲击引起的波动响应值，横坐标表示波动持续的响应期。因PM10浓度值是表征空气质量的反向指标，值越大空气质量越差，所以当波动响应值为正，表示受影响城市PM10浓度值提高，是一种负效应。相反，波动响应值为负，表示受影响城市PM10浓度值降低，是一种正效应。

图3显示所有城市PM10浓度的变化随自身冲击的响应均呈非线性函数的变化趋势，大体上经过10期之后收敛到0。除了惠州收敛速度较为均匀之外，其他城市在前4期收敛较快，第4期之后收敛较慢。这说明初始阶段所有城市的PM10无一例外都受到城市自身的影响，这种影响是一种负效应，也就是一个新息冲击会导致城市空气质量的下降，随后这种内源作用下降，外围城市的影响逐渐显现。对比各城市内源作用的程度，内源作用最强的是广州，响应系数初始值为0.17，其他8个城市的自我响应系数初始值均在0.06左右。

跨域影响有正负以及正负转换3种效应，在珠三角9城市空气质量具有格兰杰因果关系的城市对中，对脉冲新息的响应出现了15个正效应(65%)，5个负效应(22%)，3个正负效应转换的情况(13%)(表4)。据李婕等研究表明珠三角9城市在2002～2012年单个城市的空气质量上升[15]。跨域城市间普遍具有正向的影响效应，说明城市个体空气质量的改善对区域其他城市空气质量的改善具有影响。但从横向对比看，长期以来，广州，东莞和佛山是珠三角区域空气质量相对较差的地区，该地区跨域影响的情况如何？脉冲响应分析的结果显示该区域对外产生的是一种正效应，说明这3个城市空气质量的一个残差标准差的变化，会降低相应城市的PM10浓度。广佛莞3个城市的地形和气象等不利于大气污染物的扩散，相反该区域还有吸纳外源污染物的可能，从而呈现一种正的影响效果。

图3 珠三角9城市PM10浓度的自我响应

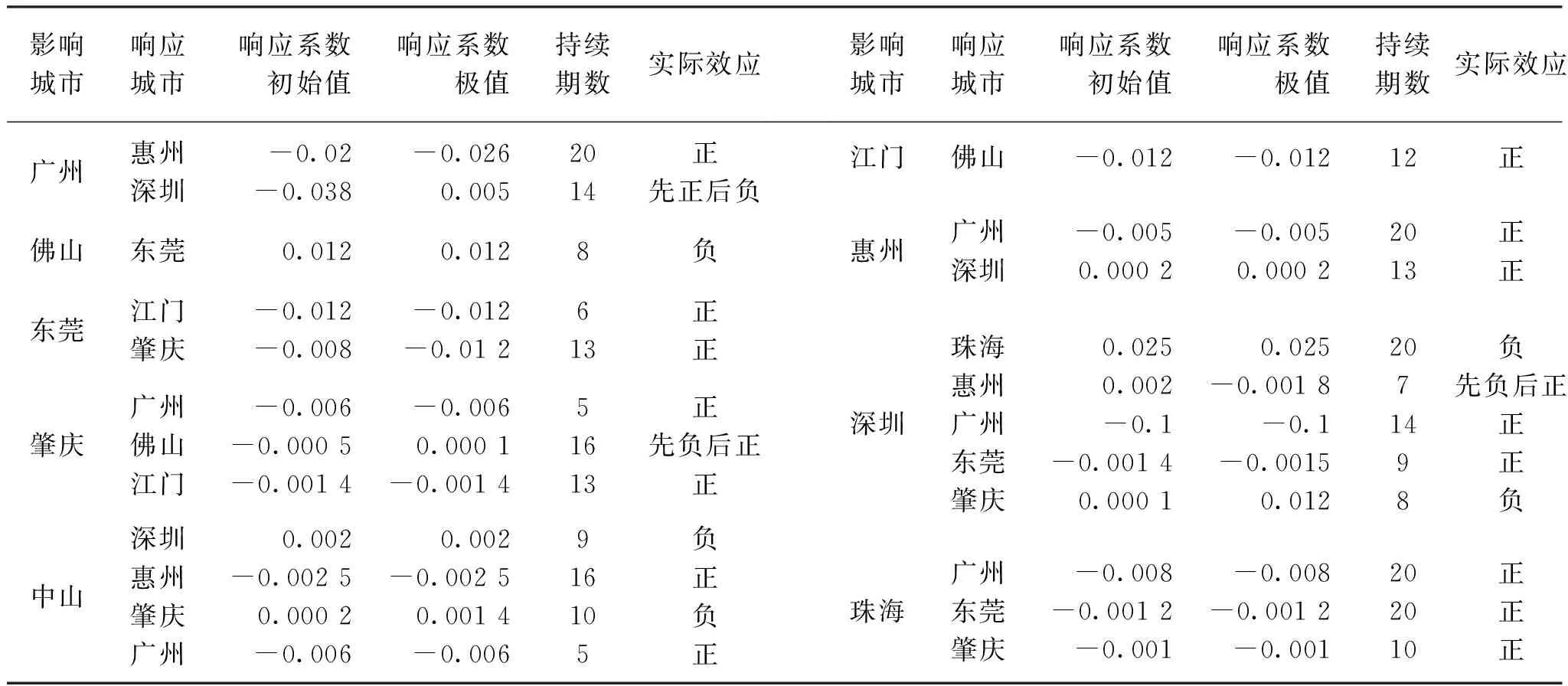
影响城市响应城市响应系数初始值响应系数极值持续期数实际效应广州惠州深圳-0.02-0.038-0.0260.0052014正先正后负佛山东莞0.0120.0128负东莞江门肇庆-0.012-0.008-0.012-0.012613正正肇庆广州佛山江门-0.006-0.0005-0.0014-0.0060.0001-0.001451613正先负后正正中山深圳惠州肇庆广州0.002-0.00250.0002-0.0060.002-0.00250.0014-0.006916105负正负正影响城市响应城市响应系数初始值响应系数极值持续期数实际效应江门佛山-0.012-0.01212正惠州广州深圳-0.0050.0002-0.0050.00022013正正深圳珠海惠州广州东莞肇庆0.0250.002-0.1-0.00140.00010.025-0.0018-0.1-0.00150.0122071498负先负后正正正负珠海广州东莞肇庆-0.008-0.0012-0.001-0.008-0.0012-0.001202010正正正

值得特别关注的是，局部城市对之间的负影响效应(表4)。具体是东莞对佛山，深圳对中山，肇庆对中山，珠海对深圳，肇庆对深圳的脉冲响应为负。这种负的单向影响往往发生在有一定距离的两个城市而不是相邻城市。所以珠三角城市空气质量的负影响并不是严格按照传染型扩散模式而发生。这说明PM10的远程输送也是存在的。

另外看3对正负效应转化的城市，其中深圳对广州的脉冲响应是先正后负，佛山对肇庆，惠州对深圳的响应则是先负后正。这种效应转化的情况说明珠三角城市空气质量的影响出现了两种模式。其中深圳对广州的响应关系代表了PM10高浓度值城市对低浓度值城市的影响(定义为模式I)。相应的事实理解为广州先吸纳外部城市的污染物，然后再对外扩散加重对应城市污染物浓度。所以对外影响表现为先正后负。佛山对肇庆的响应关系代表了PM10低浓度值城市对高浓度值城市的影响(定义为模式II)，相应的事实理解为肇庆污染物扩散在先，造成下风向城市污染物浓度上升，随后以更大的环境容量稀释佛山扩散出的污染物，表现为先负后正的效果。

4 结论

通过珠三角9城市空气质量的VAR模型构建和分析，得到的主要结论有：

(1)2002～2012年可吸入颗粒物(PM10)是珠三角地区城市空气污染首要污染物，用PM10浓度表征城市空气质量具有典型意义。采用PM10浓度周平均值作为研究城市空气质量的区域影响是适宜的。

(2)珠三角9城市在2002～2012年空气质量的动态变化特征是城市个体的自我影响强度远远超过跨域影响强度。9城市的自我响应是负效应，但城市间具有正，负或正负转换三种效应。

(3)总体而言，珠三角9城市间空气质量的影响特征是以单向性，非邻近性影响为主。南部沿海城市影响范围普遍大于北部城市的影响范围。

(4)部分PM10浓度高值或低值城市的对外影响效应出现了正负转化的模式。PM10浓度高值城市向低值城市的影响是先正后负，PM10浓度低值城市向高值城市的影响是先负后正。前者揭示了PM10浓度高值城市先吸纳外源污染物，然后再扩散，而后者则相反，PM10浓度低值城市先扩散污染物，然后再吸纳外源污染物。结合两种模式可以说明，在一定的区域范围内，城市个体的空气质量难以独善其身。

(5)对照珠三角城市空气质量相互作用的原有研究，珠三角城市的跨域影响已经成为共识，污染物浓度处于高位的城市倾向于对外产生不良影响，例如广州。但是本文的研究却发现并不是所有城市间都会发生空气质量相互作用，并且广州的自我影响强度居珠三角各城市之首，对外的空气质量影响范围并不大，甚至对外产生了正的影响效果。之所以出现这样的出入，是因为本文研究所运用的VAR模型揭示的变量间相互关系是一种宏观层面的长期均衡关系，而基于数值模拟的变量间相互关系往往是一种微观层面的短期关系。总之，珠三角城市的相对位置和局部地理条件存在差异，对珠三角城市空气质量的区域性影响不能一概而论。

[1]ByunBW，ChingTKS.SciencealgorithmsoftheEPAmodels3communitymultiscaleairquality(CMAQ)modelingsystem[M].UnitedStatesEnvironmentalProtectionAency，1999，EPA.

[2]徐祥德，周秀骥，施晓晖.城市群落大气污染源影响的空间结构及尺度特征[J].中国科学D辑：地球科学，2005，35(增刊Ⅰ)：1-19.

[3]YeBM，JiXL，YangHZ，etal.ConcentrationandchemicalcompositionofPM2.5inShanghaifora1-yearperiod[J].AtmosphericEnvironment，2003，37(4)：499-510.

[4]余纬，罗栩羽，范绍佳，等.珠三角一次重空气污染过程特征分析及数值模拟[J].环境科学研究，2011，24(6)：645-653.

[5]胡晓宇，李云鹏，李金凤，等.珠江三角洲城市群PM10的相互影响研究[J].北京大学学报：自然科学版，2011，47(3)：519-524.

[6]王淑兰，张远航，钟流举，等.珠江三角洲城市间空气污染的相互影响[J].中国环境科学，2005，25(2)：133-137.

[7]汤惠君.广州市大气污染分布规律[J].地理研究，2004，23(4)：495-503.

[8]沈家芬，冯建军，谢春玲，等.广州市PM10的时空变化特征分析[J].生态环境，2008，17(2)：553-559.

[9]马民涛，刘洁，廉婕，等.广州市大气环境演变过程及其控制要素的因子分析[J].环境工程，2013，31(6)：62-66。

[10]FacundoA，MatthewAC，RobertJRE，etal.InSearchofEnvironmentalSpillovers[J].(2009)TheWorldEconomy.doi：10.1111/j.1467-9701，2008，01160.x.，136-163.

[11]HaoJiming，HeKebin，DuanLei，etal.AirpollutionanditscontrolinChina[J].Front.Environ.Sci.Engin.China，2007，1(2)：129-142.

[12]张晓峒.计量经济学[M].天津：南开大学出版社，2014.

[13]赵进文，范继涛.经济增长与能源消费内在依从关系的实证研究[J].经济研究，2007(8)：31-42.

[14]刘海兵，刘丽.工业化、城镇化与农业现代化互动关系实证研究[J].统计与决策，2014(22)：98-101.

[15]李婕，滕丽.珠三角城市空气质量的时空变化特征及影响因素[J].城市观察，2014(5)：85-95.

ANALYSIS ON REGIONAL EFFECTS OF AIR QUALITY INTERACTION ACROSS CITIES IN PEARL RIVER DELTA

TENG Li，LU Jun

(SchoolofGeographicalScience，GuangzhouUniversity，Guangzhou510006，Guangdong，China)

The Interaction of air quality across the cities exists objectively as a consequence of air pollution spread around.It is meaningful to do some research on regional effects in which both cross-border and intra-city effect involved at the level of administrative units for government making the environmental governance policy and building the mechanism of ecological compensation between the different administrative districts.The article builds the VAR model composed of nine cities in the Pearl River Delta，based on the daily data of API of the cities from 2002 to 2012 year，which is from the Guangdong Province Environmental Information Integrated publishing platform.The results of the Granger Causality test and the impulse response analysis show there exist interaction of air quality intra-city and inter-city.The interaction degree of intra-city is generally stronger than that of inter-city.It is seen that unidirectional influence is high up to 84% and the bi-directional effect only accounts for 16%.The cross-border effects of air quality are happened between the two cities no matter whether they share the common geographical boundary or not.However，such effects occur much more in non-adjacent domain than in adjacent domain.The proportion of the former is 58% while of the later is 42%.Much more cities are influenced by the cities on the south of Pearl River Delta，rather than by those on the north of the region.The regional effects of those cities which satisfied the test of Granger Causality are identified to three kinds which positive，negative or transforming between positive and negative effect.and their proportions are 65%，22% 13% in proper sequence.Specially，the transforming between positive and negative effect reveals the two different interaction processes.

air quality；air pollution index；cross-border effect；VAR model

2015-10-11；

2015-11-18．

教育部人文社会科学项目：“资源溢出下的区域经济增长机理和对策”(12YJC790176)资助.

滕丽(1972-)女，云南省大理人，副教授，博士，主要研究方向为经济地理与区域发展.

X513

A

1001-7852(2015)06-0001-07