单壁碳纳米管储氢的统计理论模型

张 帆

单壁碳纳米管储氢的统计理论模型

张 帆

（沈阳市化工学校，辽宁 沈阳 110122）

氢能是一种洁净的可再生的能源，从长远的观点看，氢能的发展与利用能够使能源结构发生重大变化。一些研究结果表明，碳纳米管是一种很有前途的储氢材料，并且这已成为纳米材料应用研究中的一项热点内容。尽管在碳纳米管储氢方面已有一些实验结果，但是就其储氢机理的研究还很不深入，特别是储氢量的理论公式还难以见有报道。从碳原子对氢分子的吸附作用出发，提出统计理论模型，得出了储氢量公式，并与一些实验结果基本符合。这为碳纳米管储氢研究提供了理论依据。

碳纳米管；储氢；统计模型；内能；熵

碳纳米管是继富勒烯之后，人们发现的一种全新的碳单质。碳纳米管分为多壁碳纳米管和单壁碳纳米管，它们分别于1991年和1993年由日本电子显微学家Iijima发现[1,2]。由于碳纳米管具有奇异的物理和化学性质， 因此它已呈现了广阔的应用前景[3-6]，特别是利用碳纳米管储氢已成为近年来的一项热点研究内容。在这方面有一些代表性的研究结果[7-15]。氢能是一种理想的低污染或无污染的车用能源，国际上公认在不久的将来氢燃料电池汽车将是解决城市大气污染的最重要途径之一。氢作为能源有几大优点，首先，氢的储量极为丰富。由于每个水分子含有两个氢原子，而水覆盖了地球表面的75%，由此计算，地球上平均每100个原子中就有17个氢原子，故可谓是取之不尽、用之不竭。其次，氢燃烧时除产生极少量氮氧化合物外，不放出其它污染物，如果使氢在燃料电池中燃烧则不产生任何污染，只生成水，以至可循环往复不止。再有，氢的放热效率很高，这正是液氢被用作航天器燃料的原因。人们知道，储氢是氢能利用的主要环节，美国能源部（Department of Energy）通过研究表明：应用于氢燃料电池汽车上的储氢材料必须同时达到6.5%(wt)以上的重量储氢量 62kg/m3以上的体积储氢量。1997年，美国可再生能源实验室的Dillon等人进行了储氢实验[16]，Dillon等人在研究了各种储氢方法后指出，单壁碳纳米管是目前唯一可能达到这一指标的储氢材料，这吸引了众多的研究者的关注，单壁碳纳米管的储氢研究也随之全面展开。值得指出的是在碳纳米管储氢研究中仍有许多问题亟待解决，如理论研究与实验研究比较还十分滞后，储氢机理仍在探索阶段，储氢量的定量表达式更难见有报道。对此，本文从碳纳米管对氢的吸附作用出发，建立了碳纳米管储氢的统计理论模型，得出了储氢量的定量表达式，其结果与一些实验结果基本吻合。这无疑对碳纳米管储氢的实验和理论研究提供了必要的理论依据。

1 单壁碳纳米管储氢的统计理论模型

以1 g单壁碳纳米管达到最大储氢量时吸附的NH2个H2分子为研究对象，不考虑H2分子存入管及管之间的间隙中的过程，只考虑这NH2个H2分子被吸附前后状态函数的变化。设氢被吸附前为α相，被吸附后为β相，利用相变及其平衡理论，建立储氢量表达式。

1.1α相氢气的态函数

α相的氢气可视为理想气体，遵守麦克斯韦—玻耳兹曼统计分布，而每个氢气分子可视为空间线性谐振子，有平动、转动和振动三个自由度，加上原子核外电子的运动，氢气分子的熵应包括平动熵、转动熵、振动熵和电子熵。但由于氢气分子振动特征温度较高，且氢气分子的双原子电子态为 Σ1态，电子特征温度更高，故常温或低温条件下，振动熵和电子熵完全可以忽略不计，只考虑其平动熵和转动熵。

式（2）、（3）中，N为系统气体分子总数，k为玻耳兹曼常数，T为系统的热力学温度。由于内能和熵都是广延量，可分步求之，然后加和。

H2分子的平动配分函数为：

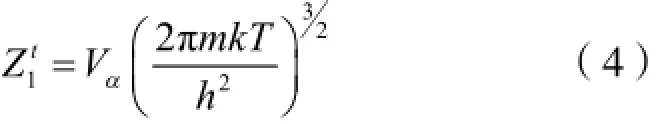
式（4）中，Vα为α相氢气的体积，m为 H2的质量，h为普朗克常数。将式（4）代入式（2）、（3）中，可得：

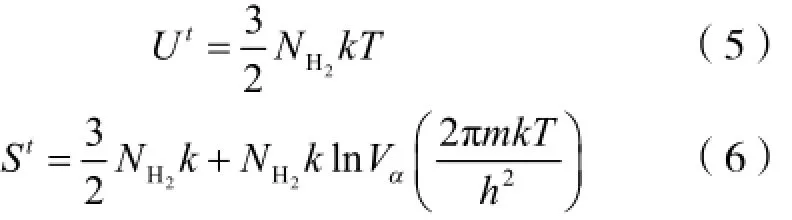
H2分子转动配分函数，要考虑两个氢原子核自旋平行（正氢）和反平行（仲氢）两配分函数和共同作用的结果。分别为

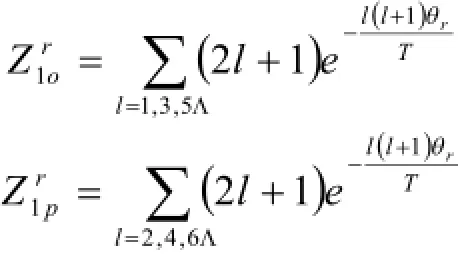
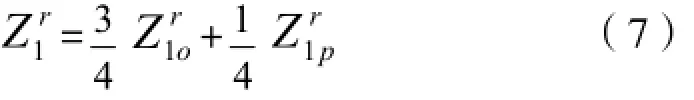
H2分子转动特征温度为85.4 K，且各转动能级近似连续，求和可用积分代替，由式(7)有：

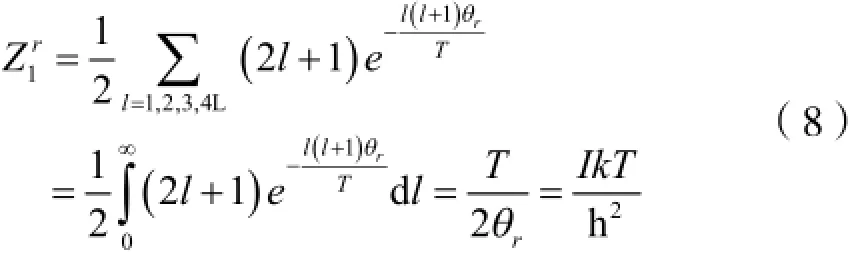
式(8)代入式(2)、(3)中，得

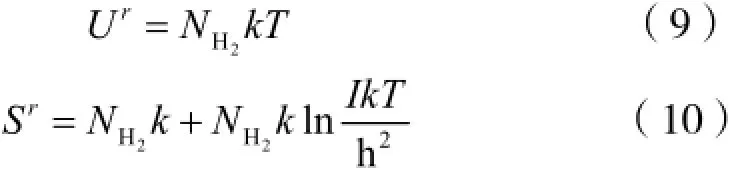
由式(5)、(6)、(9)和(10)，得α相时系统内能和熵的表达式为

1.2β相氢气态函数的改变

先考虑由于自由度改变引起态函数的变化。

H2由游离的α相到吸附的β相，H2的平动受到极大的限制，此处我们近似认为平动自由度消失，内能和熵的增量分别为：

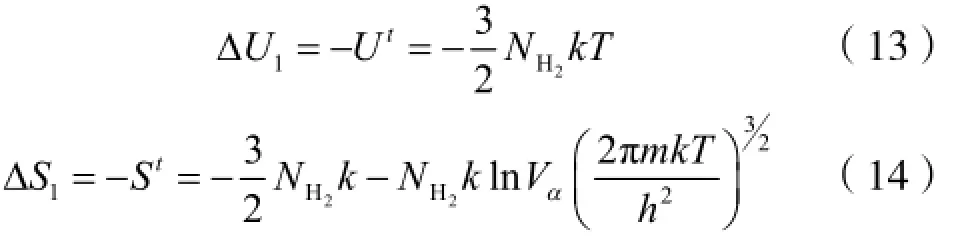
下面考虑吸附过程中由于吸附作用引起的态函数变化。

每个H2分子被吸附时，必然有一个吸附能，取这一能量平均值为u，则该作用引起系统能量增量为：

其次，由于本模型考虑的是在一定温度和压强条件下，达到最大储氢量时有个H2分子，故可以认为平衡时碳原子共提供个吸附位，且所有吸附位均被占据，而由于管的对称性决定每个吸附位彼此之间不应该有所差别，即每个吸附位应位于碳原子附近的等价位置上，设1克碳纳米管含C原子数为因此吸附过程引起的位形熵增量为

由式(13)-(16)可知，吸附过程总内能及熵的变化为：

另外，α相时气体按理想气体处理，满足

式（19）中，P为系统压强，R为气体常数，为阿夫加德罗数。因为β相时体积相比很小，所以可忽略。

吉布斯函数为

在等温等压过程中吉布斯函数的变化为

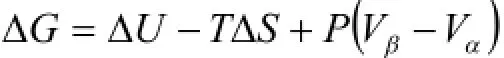
将式（17）-（19）代入上式，知

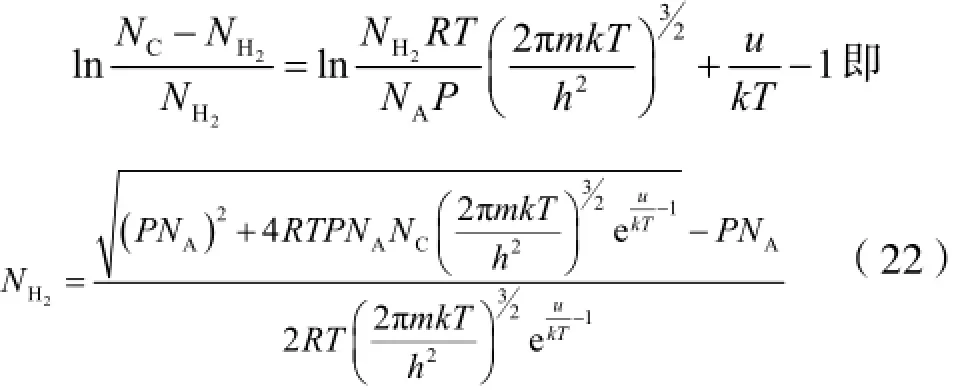
1.3 吸附能u与温度T的关系

由式（22）得

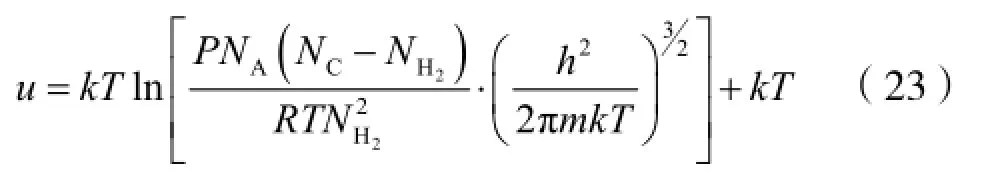
利用式（23），并参考其他学者的理论计算结果[17-20]，可得表1。

表1 由各理论计算值算得的u值Table 1 Values based on different theories

由上表数据可作出Tu- 关系曲线，如图1。

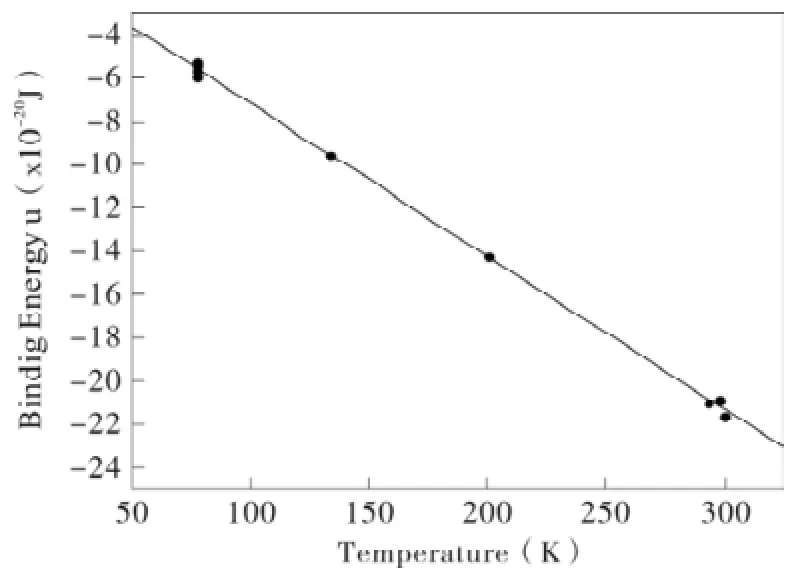
图1 Tu- 的关系Fig.1 The relation of Tu-

从图1看出，u为负值且与T成一次函数关系，在图1中利用线性拟合，便可得到一条理想的直线，其斜率为：

1.4 储氢量定量表达式

将式（22）中H2分子数转化为1克单壁碳纳米管存储的H2的质量则式（22）化为：

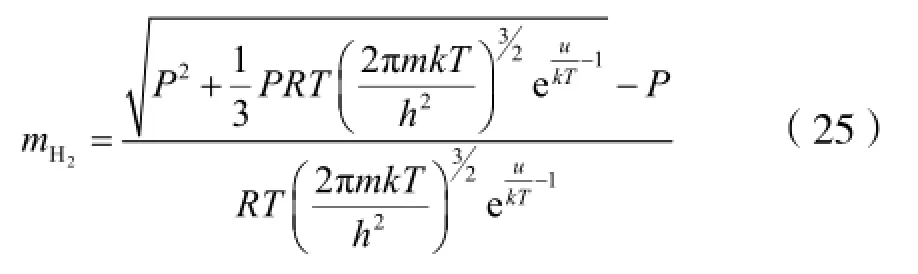
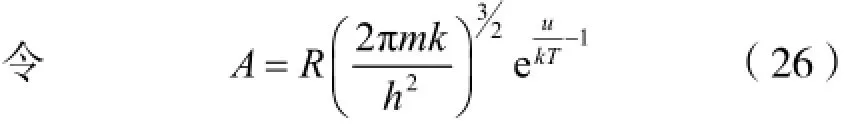
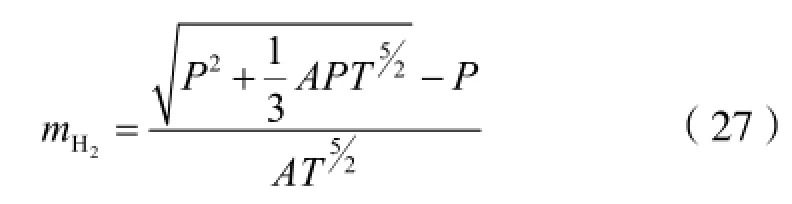
式（27）中P的单位为Pa，T的单位为K，单位为g。上式即为储氢量随温度、压强等参量变化的解析式。

2 分析讨论

2.1 吸附能与温度关系

对得到的吸附能u可以从物理上给出如下解释：吸附能是对H2分子有约束作用的能量，故必为负值，这才能起到吸附的作用；因为分子平均平动动能与T成正比，因此对H2分子平动产生“束缚”作用的吸附能u也应与T成线性关系。这是本模型的一条重要结论，也是使本文得到的储氢量公式能够定量计算的一个主要原因。

2.2 储氢量和温度的关系

图2 mH2- T关系曲线Fig.2 Relation curve of mH2- T

2.3 储氢量和压强的关系

由式（27）知，储氢量mH2随压强P的增加而增大。这是因为压强越大，分子与碳纳米管的碰撞频率越大，此时H2分子被碳纳米管吸附的机会就越大。储氢量mH2与压强P的关系曲线见图3。从该图还能看出，在同一压强下，温度越高则储氢量越低，这一规律也与实验相符合。

图3 关系曲线Fig.3 Relation curve of

2.4 储氢量计算值与实验值的比较

由式（27）得到的mH2值与实验值[21-23]比较，得表2。

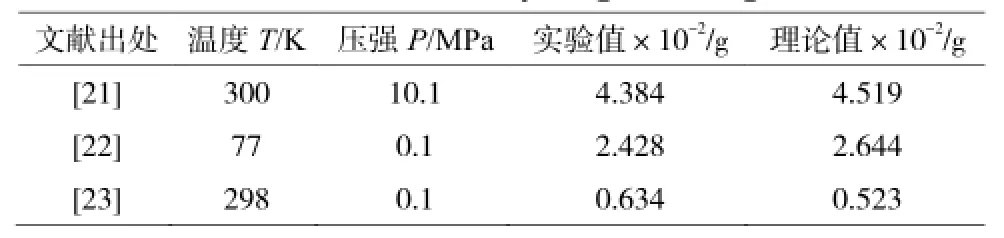
表2 储氢实验值与本模型理论值的比较Table 2 Comparison of experimental value and theory value of this model for hydrogen storage

由此可见，理论计算的结果与实验值基本符合。

3 结 论

（1）本文从碳纳米管与氢分子的吸附作用出发，利用相变及其平衡理论得出了1克碳纳米管储氢量的定量表达式，由该式计算的理论结果与实验结果基本相符，这为碳纳米管的储氢研究提供了理论依据。

（2）从得到的储氢量表达式知，储氢量随温度升高而降低而随压强升高而提高，这也为提高储氢量指出了方向。

（3）文中得出了碳纳米管与氢分子的吸附能u和温度T的关系，并且=常数，这符合物理规律，同时它极大的简化了储氢量定量的计算。

［1］ Iijima S. Helical microtubules of graphite carbon[J]. Nature, 1991,354:56-58.

［2］ Iijima S,Ichihashi T. Single-shell carbon nanotubes of 1-nm diameter[J]. Nature,1993,363:603-605.

［3］ Wang Z L, Poncharal P, de Heer W A. Measuring physical and mecha- nical properties of individual carbon nanotubes by in situ TEM[J].J.Phys.Chem.Solids,2000,61:1025-1030.

［4］ Hamada N, Sawada S,Oshiyama A. New one-dimensional conductorgraphi-tic microtubules[J]. Phys.Rev.Lett.,1992,68:1579-1581.

［5］ Rao A M, Richter E, Bandow S, et al. Diameter-selective Raman Scat-tering from vibrational models in carbon nanotubes[J].Science, 1997,275:187-191.

［6］ 郭连权.碳纳米管的物性及应用.人工晶体学报.2002,31（2）:164-168.（Physics properties and applications of carbon nanotubes [J].Journal of synthetic crystals,2002,31(2),164-168.

［7］ Stan G, Cole M W. Hydrogen adsorption in nanotubes[J]. Low Temp.Phys.,1998,110:539-544.

［8］ Yang R P. Hydrogen storage by alkali-doped carbon nanotubesrevisited[J]. Carbon,2000,38:623-641.

［9］ Seung M L, Young H L. Hydrogen storage in single-walled carbon nanotubes[J]. Appl.Phys.Lett.,2000,76:2877-2879.

［10］Liu C, Fan Y Y, Liu M et al. Hydrogen storage in singal-walled carbon nanotubes at room temperature[J]. Science, 1999, 285: 1127-1129.

［11］Elzbieta Frackowiak, Francois Beguin, Electrochemical storage of energy in carbon nanotubes and nanostructured carbons[J]. Carbon, 2002, 40: 1775-1787.

［12］Qin X., Gao X P.,Liu H.,et al,Electrochemical Hydrogen Storage of Multiwalled Carbon Nanotubes[J].Electrochemical and Solid-State letters,2000,3:532-535.

［13］Hyoung SeukYouna,Hojin Rtna,Tae-Hwan Chob,Weon-Kyung Choi a,Purity enhancement and electrochemical hydrogen storage proper ty of carbon nanobers grown at low temperature[J]. International J ournal of Hydrogen Energy,2002, 27:937-940.

［14］Nützenadel C., Züttel A., Chartouni D.,and Schlapbach L., Elec trochemical storage of Hydrogen in Nanotube Materials[J].Electroc hemical and Solid-State Letters，1999，2：30-32.

［15］Dai G P., Liu M., Chen D M.,Hou P X.,Tong Y.,and Cheng H M., Electrochemical Charge-Discharge Capacity of Purified Single-walled carbon nanotubes[J]. Electrochemical and Solid-State Letters，2002，5：13-15.

［16］Dillon A C, Jones K M, Bekkedahl T A. Storage of hydrogen in single-walled carbon nanotubes[J].Nature,1997,386:377-379.

［17］Wang Q,Johnson JK.Molecular simulation of Hydrogen Adsor-ption in single-walled Carbon Nanotubes and Idealized Carbon Slitpores[J].J Chem Phys.,1999,110:577-568.

［18］Wang Q,Johnson JK.Optimization of Carbon nanotubes Arrays for Hydrogen Adsorption[J].J Chem Phys B.,1999,103:4809-4813.

［19］Darkrim F,Levesque D.Monte Carole simulations of hydrogen adsorption in single-walled Carbon nanotubes[J]. J Chem Phys.,1998,109:4981.

［20］Gu C,Gao GH,Yu YX,et al.Simulation Study of hydrogen Srorage in single Walled Carbon nanotubes[J].International Joural of Hydrogen Energy., 2001, 26(7):691-696.

［21］Liu C, Fan Y Y, Liu M, et al. Hydrogen storage in single-walled carbon anotubes at room temperature[J].Science,1999,286:1127-1129.

［22］Nishimiya N,Ishigaki H,Takikawa H,et al.[J].J Alloys and Compounds,2002, 339:275.

［23］Ristchel M,Uhlemamm M,Gutfleisch O,et al.Hydrogen Storage in different on nanotubes[J].Appl Phys Lett.,2002,80(10):2985.

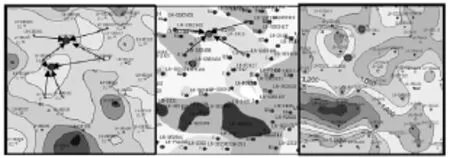
图4 注采关系与剩余油分布关系Fig.4 Relationship between injection-production ratio and residual oil distribution

4 结 论

喇北东块三类油层三元复合驱垂向上储层的韵律结构与剩余油分布密切相关，垂向剩余油主要具有三种分布规律，即顶部富集型、均匀驱替型和底部富集型，三种类型分别具有不同的剩余油分布特征。平面剩余油分布主要受沉积微相和储层特征、平面非均质性和注采关系的控制。沉积微相决定剩余油的分布，储层特征、平面非均质性和注采关系控制剩余油的富集程度。

参考文献：

［1］ 董冬，陈洁，邱明文.河流相储集层中剩余油类型和分布规律［J］.油气采收率技术，1999，6（3）：39-46.

［2］ 李春英，吴晓东，李淑霞.特高含水深度开发阶段调整挖潜技术政策界限——以胜坨油田坨28断块沙二段7—8单元为例［J］.油气地质与采收率，2010，17（6）：97-100.

［3］ 王军.中原油田濮 53 断块流动单元划分与剩余油分布研究［D］.北京：中国地质大学（北京），2007.

［4］ 蔡忠，曾发富.临南油田沉积微相模式及剩余油分布［J］.石油大学学报：自然科学版，2000，24（1）：44-47.

［5］ 刘伟，罗小刚.细分沉积微相研究剩余油分布规律［J］.科学技术与工程，2011，11（27）：6 705-6 709.

［6］ 具海啸，周博. 喇北东块萨三组沉积特征研究［J］. 重庆科技学院学报（自然科学版），2012，14（3）：31-33.

Statistical Theory Model of Hydrogen Storage in Single-walled Carbon Nanotubes

ZHANG Fan
（Shenyang Chemical Industry School, Liaoning Shenyang 110122, China）

Hydrogen energy is an environmentally friendly and renewable energy source. The development and application of hydrogen energy will bring great changes for the structure of energy sources from the long view. Carbon nanotubes were reported to be very promising materials for storing hydrogen form some research finding, which has been a hot spot in the applied research field of studying nano materials. Although many experimental results for hydrogen storage in carbon nanotubes were reported, corresponding theoretical investigation of adsorption mechanisms have almost not developed and it is difficult to find the theoretical equation of hydrogen storage quantity in particular. In this paper, statistical theory model on the basis of interaction between hydrogen molecules and carbon atoms was presented, and the formula of hydrogen storage quantity was obtained, which is almost in agree with the experiment value. The conclusion can provide theoretical reference for studying hydrogen storage in carbon nanotubes.

Carbon nanotubes；Hydrogen storage；Statistical model；Internal energy；Entropy

O 73；O 799

： A

： 1671-0460（2015）04-0792-05

2014-10-20

张帆（1957-），男，辽宁沈阳人，高级讲师，1982年毕业于沈阳机电学院应用物理专业，现任沈阳市化工学校教师。