一种CPM信号与PSK类信号的调制识别算法
2015-01-10吕平,高勇
吕 平,高 勇
(四川大学电子信息学院,四川成都610065)
一种CPM信号与PSK类信号的调制识别算法
吕 平,高 勇
(四川大学电子信息学院,四川成都610065)
提出了一种基于分形盒维数及二次方谱特征的方法,对由CPM与PSK类信号组成的信号集进行调制识别分类。首先提取信号集内各待识别信号的分形盒维数特征,将CPM和OQPSK识别出来;然后对信号集中剩余信号提取相应的二次方谱离散谱线特征依次区分出BPSK、UQPSK和QPSK;最后根据决策树原理设计分类器,实现信号集内信号的识别。仿真结果表明,该算法对信号集内的信号在信噪比达到3 dB以上条件下正确识别率可达到90%以上。
连续相位调制;分形盒维数;决策理论;调制识别
0 引言
连续相位调制(Continuous Phase Modulation,CPM)信号,凭借其包络恒定、相位连续等优越性能在卫星通信领域已取得较广泛的应用[1,2],而且在未来的移动无线通信系统中具有广阔的应用前景[3],研究此类信号的调制识别算法具有重要意义。
Aulin T和Sundberg C[4,5]等人分析了连续相位调制方法,为CPM的研究奠定了基础。文献[6]提出了一种基于复杂度特征的调制识别算法,对ASK、FSK和PSK信号进行了识别,但所用到的分类器设计较为复杂,且在信噪比达到5 dB条件下信号集内尚有过半数信号的正确识别率在90%以下;文献[7]通过分析BPSK、QPSK、OQPSK和UQPSK 4种信号的二次方谱及四次方谱结构,提出了对BPSK、QPSK和OQPSK信号的分类方法,但并未给出UQPSK的识别方法,而且没有作信号正确识别率统计实验;文献[8]针对UQPSK信号提出了一种基于提取信号二次方谱离散谱线特征的调制识别算法,算法要在信噪比达到5 dB以上才有90%以上识别率。在上述基础上,扩大了待识别信号集范围(延伸至CPM信号),所提出的算法可在更低信噪比(≥3 dB)条件下完成对信号集内信号的正确识别。仿真结果表明,在信噪比大于3 dB时,集内信号的正确识别率能达到90%以上。
1 信号模型
1.1 连续相位调制(CPM)信号
CPM信号的一般表达式[9]为:
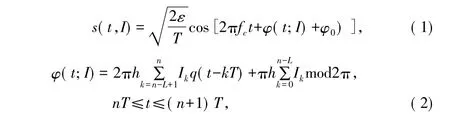
式中,T为码元间隔,ε为T内的符号能量,fc为载波频率,φ0为载波初始相位。I为发送的M进制符号序列向量,其中每一个符号元素Ik的取值范围为{±1,±3,…,±(M-1)},h=K/P(K,P为互质的整数)为调制指数,L为关联长度(成形脉冲的持续时间);q(t)为成形脉冲g(t)的积分,常称q(t)为相位响应,q(t)满足以下性质:
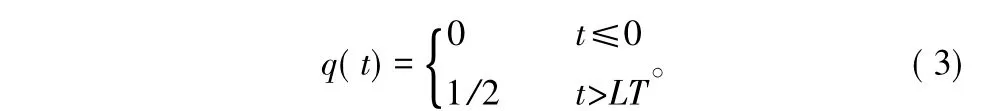
1.2 PSK类信号
M进制PSK信号的一般表达式为:

式中,Tb为码元宽度,g(t)为成形滤波器波形,滤波器滚降系数α可根据需要进行设置,fc1为载波频率,θm为M个可能的相位取值,且在同一码元内取值相同。
OQPSK信号是错开半个码元的QPSK信号,其I/Q两路信号只存在0和±π/2的相位跳变而不存在±π的相位跳变,其信号模型为:

式中,A为信号幅值,I2n和I2n+1为码元符号,g(t)为成形滤波器波形,T为码元间隔,fc为载波频率。
UQPSK信号可以看作是I/Q两路功率不等的QPSK信号,也可以看作是两路正交传输的独立二进制比特流,而这两路数据流由于码速率或其幅度值差异导致信号能量不相等。其信号模型为:

式中,P为信号功率;an和bn为发送的两路独立二进制随机序列;fc为载波频率;T1和T2分别为I/Q两路的码元间隔,二者可能相同,也可能不同;β为 UQPSK的非平衡因子(1<β<■2)。
2 信号自动调制识别方案
待识别的信号集为{CPM、BPSK、QPSK、OQPSK和UQPSK}。从信号的分形盒维数特征和瞬时特征出发,提出了3个特征参数可将信号识别出来。
2.1 参数设计
2.1.1 分形盒维数D
分形维数是分形理论中非常关键的参数,它定量地描述了某个分形集的不规则程度[10],通信信号是一种时间序列,因此可以对其用分形来进行有效刻画。Hausdorff维数是各种分形维数中最基本的一种,但在分形理论及其应用中,一个给定的分形的Hausdorff维数的计算较为复杂,这一缺点限制了其在实际中的应用。而盒维数由于计算简单且易于经验估计,故在实际中多采用之。
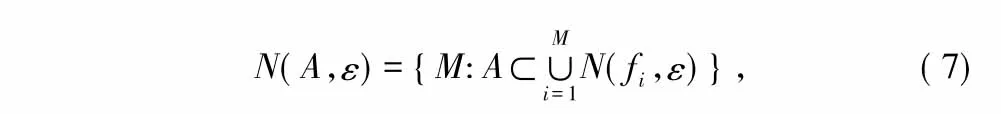
式中,f1,f2,…,fM是F中的不同点。若存在下述极限:

则称D为函数f的盒维数。其中,f

是定义在ℝ的闭集W上的连续函数。根据上述定义,对数字化离散信号点集的分维值,可通过粗视化过程简化计算盒维数值。
设f(t1),f(t2),…,f(tL),f(tL+1),L为偶数。令:
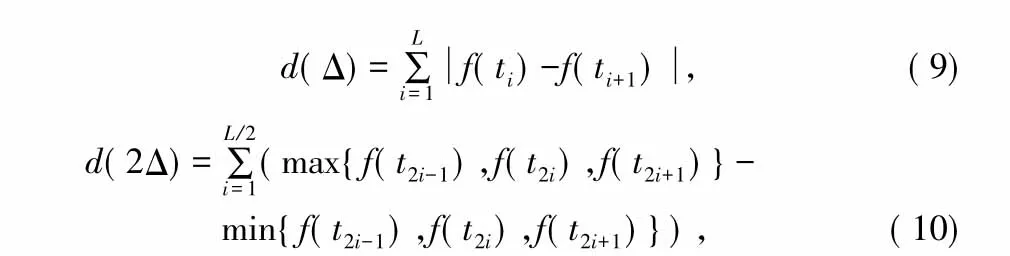
那么

基于分形盒维数的特征值分布曲线如图1所示,从图中可以很容易地看出,通过分形盒维数值这一参数,将CPM信号和OQPSK信号从信号集中识别出来是可能的,正如下文将要看到的,合理设置2个门限值,即可将CPM信号与OQPSK信号区分出来。

图1 分形盒维数特征参数D
2.1.2基于信号二次方谱线特征的参数S2
PSK类信号经非线性变换后往往具有丰富的谱线特征[7],如BPSK的二次方谱和QPSK的四次方谱含有明显的离散谱线。经过大量的仿真观察发现,QPSK类信号二次方谱不含离散谱线,故可以利用此规律以从QPSK类信号中识别出BPSK信号。基于上述分析,采用如下特征参数:

式中,Var表示求信号s的方差,E表示求其均值。S2参数用于将BPSK与UQPSK、QPSK区分开来。参数S2的特征值分布曲线如图2所示。

图2 二次方谱谱线特征参数S2
由图2可知,通过二次方谱谱线特征S2这一参数,将BPSK信号与UQPSK、QPSK区别开来是可能的,正如下文将要看到的,合理设置一个门限值,即可将BPSK信号识别出来。
2.1.3基于信号二次方谱线特征的参数λ
对于UQPSK和QPSK信号的识别参数选择,采用文献[8]的特征参数,其定义如下:

式中,R(f)=F{[r'(t)]2}为接收信号r(t)归一化处理后所得信号r'(t)的二次方谱。m为用于最大化峰值与均值差异的一个因子。
参数λ的特征值分布曲线如图3所示。

图3 二次方谱谱线特征参数λ
从图3中可以看到,通过二次方谱谱线特征λ这一参数,将信号UQPSK与QPSK区别开来是可能的,合理设置一个门限值,即可将二者分别识别出来。
2.2 分类器设计
根据对信号特征及特征提取算法的讨论和分析,提出了一种基于决策树的信号自动调制识别算法,共提取3个特征参数,设置了4个不同的门限th_d1=1.2,th_d2=1.085,th_S2=0.1,th_lumda=-17.64,其中th_d1和th_d2是对分形盒维数参数设置的门限,th_S2是对二次方谱线特征参数S2设置的门限,th_lumda是对二次方谱线特征参数λ设置的门限。通过上述门限设置完成对信号集中{CPM、BPSK、QPSK、OQPSK和UQPSK}共5种信号的识别,文中的待识别信号为经过下变频后的近似零中频信号,具体调制识别流程图如图4所示。

图4 调制识别流程图
3 算法仿真及性能分析
仿真实验条件设置如下:BPSK、QPSK和OQPSK 3种信号的码速率为100 kbps,频偏为码速率的0.06倍,采样率为带宽的4倍,脉冲成形使用升余弦滚降滤波器,滚降系数α为0.35;UQPSK信号采用两路BPSK信号叠加产生,两路的码速率均为100 kbps,同相路和正交路功率比为2∶1,其余设置同前述PSK类信号。CPM信号采用四进制,成形脉冲为升余弦滚降脉冲(滚降系数为0.35),关联长度L取为4,调制指数为2/7,码速率同样设置为100 kbps,其余设置同上述信号。参与识别的信号采样点数为8 000点,在高斯白噪声环境下,信噪比在-5~25 dB范围内变化,在每个信噪比下进行100次蒙特卡罗实验,统计不同信噪比条件下信号的正确识别率,仿真结果如图5所示。

图5 信号集内各调制信号在不同信噪比下的识别率
由图5可见,在信噪比达到3 dB以上,对待识别信号集内的5种信号的正确识别率均可达到90%以上,QPSK、UQPSK和CPM甚至在0 dB附近识别率即已达到90%以上。改变仿真参数(如码速率等)设置条件,按表1所列某一个参数的设置范围随机地调整其值,固定其余3个参数值(该固定值也要在表中所列范围内随机确定),重复上述仿真过程。
仿真结果表明,各参数在表1所示设置范围内变化时识别率仍能达到90%以上,这说明所提出的算法对信号参数的变化具有较好的适应性和良好的稳健性。
4 结束语
针对CPM信号与常用的几类PSK类信号的调制识别进行了研究,不仅扩大了待识别信号集范围,而且在更低的信噪比条件下实现了信号集内信号的正确识别分类。通过结合信号分形盒维数特征及PSK类信号的二次方谱线特征的分析,提出了一种非数据辅助的自动调制识别方法。该算法除了具有简单和易于实现的优点外,还对接收信号的载波频偏、码速率、成形滤波滚降系数以及CPM信号的调制指数具有较好的适应性,说明算法具有较高的稳健性。
[1]王勇军,彭华.卫星回传链路CPM信号调制识别研究[J].信息工程大学学报,2013,14(3):347-352,370.
[2]王勇军,彭华.卫星回传链路CPM信号符号速率估计[J].信息工程大学学报,2014,15(1):74-79.
[3]张怡,张航,唐成凯.基于连续相位调制的OFDM信号研究[J].西北工业大学学报,2007,25(6):834-837.
[4]Aulin T,Sundberg C.Continuous phase modulation—Part I:Full response signaling[J].IEEE Transactions on Communications,1981,29(3):196-209.
[5]Aulin T,Sundberg C.Continuous Phase Modulation-Part i:Full Response Signaling[J].Communications,IEEE Transactions on,1981,2(3):196-209.
[6]吕铁军,郭双冰,肖先赐.基于复杂度特征的调制信号识别[J].通信学报,2002,23(1):111-115.
[7]和昆英,李麒,郭虹,等.BPSK、QPSK与OQPSK、UQPSK调制识别方法初探[J].微计算机信息,2006,4(10):286-288.
[8]王晨雪,彭淼,高勇.非平衡相移键控信号的调制识别算法研究[J].无线电工程,2013,43(9):28-32.
[9]Proakis JG,SalehiM.Digital Commuications[M].张力军译.北京:电子工业出版社,2011:82-84.
[10]谢和平,薛秀谦.分形应用中的数学基础与方法[M].北京:科学出版社,2005:81-88.
An Algorithm for M odulation Recognition of Continuous Phase M odulation Signals and PSK-type Signals
LV Ping,GAO Yong
(College of Electronics and Information Engineering,Sichuan University,Chengdu Sichuan 610065,China)
A method based on fractal box dimension and square spectrum line features is proposed perform modulation recognition for the signal set consisting of continuous phasemodulation(CPM)and PSK-type signals in this paper.Firstly the fractal box dimension feature of each signal to be recognized in the signal set is extracted to figure out the CPM and OQPSK signal.Then the discrete spectral lines feature of square spectrum of the remaining signals is extracted to recognize BPSK,UQPSK and QPSK in turn.Finally,the classifier is designed according to the principles of decision tree to realize the recognition for signals within the set.The simulation results show that the proposed algorithm can realize the correct recognition rate of the signals in the set of over 90%when the SNR(signal to noise ratio)is above 3dB.
CPM;fractal box dimension;decision theory;modulation recognition
TN919
A
1003-3114(2015)04-64-4
10.3969/j.issn.1003-3114.2015.04.16
吕 平,高 勇.一种CPM信号与PSK类信号的调制识别算法[J].无线电通信技术,2015,41(4):64-67.
2015-04-07
吕平(1988—),男,硕士研究生,主要研究方向:通信信号调制识别、信号处理。高勇(1969—),男,博士、教授,主要研究方向:通信抗干扰技术、阵列信号处理、信号分析与处理。
