认知无线电合作频谱感知算法研究

包志强，史园园

（西安邮电大学通信与信息工程学院，陕西西安710061）

认知无线电合作频谱感知算法研究

包志强，史园园

（西安邮电大学通信与信息工程学院，陕西西安710061）

频谱感知是实现认知无线电功能的前提条件，也是认知无线电领域的一个研究热点。近年来人们提出了很多频谱感知的方法，尤其是合作频谱感知算法日益受到人们的关注。综述了合作频谱感知技术的最新研究进展，从简单的线性信息融合算法到复杂的非线性感知算法，以及多天线合作感知等算法，通过仿真比较各种方法的检测性能，并展望未来频谱感知所面临的挑战和发展趋势。

认知无线电；合作频谱感知；信息融合；检测性能

0 引言

近年来合作频谱感知得到了广泛而深入的研究。本文主要研究内容从4个方面进行。

第一，硬判决合作感知算法［1，2］这样可以有效地解决单用户隐藏终端问题；但是该方法容易受到信道衰落的影响。文献［3－7］利用加权的思想，为各个认知用户的检测结果附加权重，这样就能够有效地避免信道环境对最终结果的影响。

第二，基于RMT随机矩阵理论，该类算法最具代表性的3种频谱感知算法，分别是MED算法［8］、基于最大与最小特征值之比［9，10］和MMED算法［11］，这些算法不同之处就在于检测统计量的构造不同，MED算法克服了门限固定的缺点，但是受到噪声不确定性的影响。基于最大最小特征值之比的算法有效地克服了噪声不确定性的影响，门限总是固定不变的。MMED算法克服了上述2种算法的缺点，不仅具有感知性能更好以及对噪声不敏感等优点，而且在认知用户较少、样本较小的情况下，也可以获得较好的检测性能。

第三，使用D－S融合规则来对各自感知节点的感知信息进行融合，如文献［12］和文献［13］的算法，改进多节点算法合并规则中未考虑单节点感知可信度或需要知道单节点的先验信息的缺点。

第四，基于模糊理论如文献［14］，多天线的合作频谱感知算法如文献［15］，频谱感知算法中的节能问题如文献［16－18］。

1 信息融合算法

1.1 硬判决融合算法

硬判决算法是信息融合算法中最简单、最基础的算法。最典型的硬判决融合方法就是“与”、“或”、“K of N”算法。硬判决算法解决了单用户频谱感知中的隐藏终端及灵敏度过高的问题。然而此方法只能适合信道条件好的环境中。

1.2 线性加权算法

常见的线性加权的方法主要是：均值加权和信噪比加权。

1.2.1 基于均值加权算法

均值加权算法类似于“K of N”原则算法，当有N个认知用户参与合作时，加权因子wi＝1/N，i＝1，2，3，...，N。认知用户将检测到的信息传送到融合中心，融合中心根据所传信息进行加权并作出最终判决，与“K of N”算法不同之处在于，均值加权中，认知用户传递的是检测到的全部信息，而不是判决结果。因此这样就能够使得融合中心能够做出更准确的判决。

1.2.2 基于信噪比加权算法

实际的通信环境中，各个认知用户所处的地理环境不同，主用户的信号经过衰落并且混合着噪声到达各认知用户的接收端，由于无线环境的复杂及人为噪声的影响，认知用户介绍到的信号的信噪比是不同的，利用各认知用户的信噪比构造其加权因子，就是信噪比加权的合作感知算法。

首先，各个认知用户的权重因子由下式所确定：

式中，γi是第i个认知用户的信噪比是N个用户总的信噪比，则wi为第i个用户的权重。然后，将权重分配给相应的用户，生成新的检验统计量Y＝

1.3 基于信任度加权算法

此算法首先定义一个模糊型指数信任度函数bij（表示第i个用户被第j个用户信任的程度），对两认知用户间的信任度进行量化处理，并通过信任度矩阵度量各认知用户测得的数据的综合信任度，以合理分配测得数据在融合工程中所占权重本文将信任度函数bij定义为满足模糊性的指数函数形式，即设：

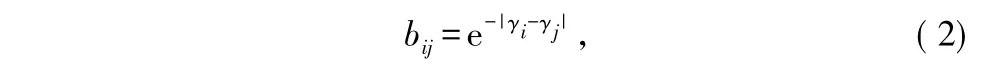
式中，γi，γj分别表示第i个用户和第j个用户的信噪比，用上述式子表示即充分利用了模糊理论中隶属度函数范围确定的优点，又避免了数据之间相互信任程度的绝对化，更符合实际环境，便于具体实施，从而使结果更加准确。权重因子表示为：

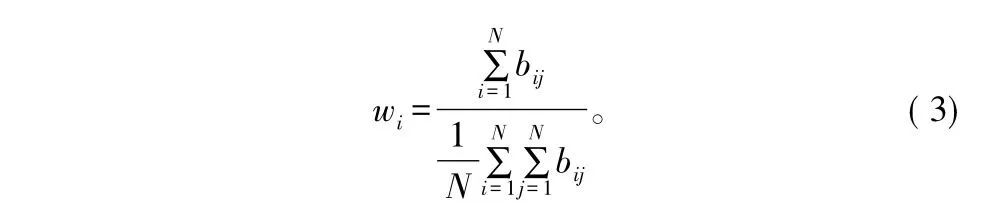
由上式可知，权值计算的基本单位是信号的指数形式，其值随着自变量的增大而逐渐减小，即随着信任度的减小而逐渐减小，与漏检概率随着信噪比的减小而逐渐减小的特性相类似，具有很好的拟合性。

1.4 基于信噪比选择加权合作算法

合作频谱感知过程中伴随着巨大的系统资源的消耗，若限制参与合作的认知用户数目，就能够减小系统资源的消耗。设置信噪比门限，使信噪比大于门限的认知用户参与合作，小于门限的用户不参与合作。该算法首先要找出最大的信噪比＝（），然后设置目标信噪比＝η，其中，η是信噪比门限，将第i个认知用户的信噪比与目标信噪比进行对比，当γi＞γth时，则参与融合，对于则不参与合作，从整体上减小了资源的消耗，这个也是频谱感知未来研究的方向之一。硬判决融合规则性能比较如图1所示。

图1 硬判决融合规则性能比较

图1参数设置为：7个认知用户参与合作，采样点数为1 000，单个认知用户的虚警概率为0.1。从图1中可以看出，“与”规则在信噪比小于－6 dB时检测概率小于99.9％，容易对授权用户产生干扰；而“或”规则在授权用户不存在时也有一半概率判定授权用户存在，造成大量空闲频段的浪费；“K of N”算法既满足虚警概率的要求，在－9 dB时检测概率为99.9％，满足要求，性能优于前两者。

图2参数设置为：认知用户接收到的信号信道环境相同，即认知用户的信噪比是相同的，认知用户数N＝12，单用户采用能量检测算法且虚警概率为Pf＝0.1，抽样数为1 000；从图2中明显看出均值加权性能明显优于“K of N”算法，这是因为“K of N”算法中融合中心仅得到了认知用户的二元判决信息，而在均值加权算法中融合中心得到了认知用户检测到的全部信息。

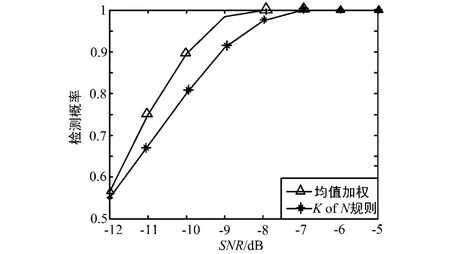
图2 均值加权和“K of N”原则仿真性能对比

图3认知用户数目N＝7，采样点数为600。从图3可以看出，在不同的信噪比的条件下，采用信噪比加权的融合算法比采用均值加权的融合算法，检测性能好。

图3 均值加权与信噪比加权性能比较

从图4可以看出，基于信任度加权算法的漏检概率明显低于其余2种算法，因为漏检概率与检测概率之和等于1，因此漏检概率越小说明检测概率越大，系统的检测性能越好。图5的参数设置为：认知用户数为10，其余条件不变。从图5中可以看出选择信噪比加权算法的检测性能与信噪比加权的算法性能基本相同，同时2个的性能优于均值加权算法。信噪比加权有10个认知用户参与合作，信噪比选择只有7个认知用户参与合作，因此后者将节省大约30％的系统能量。因此，信噪比选择合作算法既能够节省资源，检测性能也没有下降。

图4 信任度加权、信噪比加权和均值加权的性能对比图

图5 均值加权、信噪比加权、信噪比选择加权性能比较

2 非线性合作感知算法研究

所列举的非线性合作频谱感知算法主要针对接收信号协方差矩阵特性，将其特征值最为判决门限的合作频谱感知算法，不同的算法对应不同的判决门限。

2.1 最大特征值检测理论（MED）

MED算法利用随机矩阵理论中有关随机矩阵最大特征值概率分布特性理论，获得了采样协方差的最大特征值的概率分布函数。

概率密度分布函数的表达式极为复杂，没有一个紧凑的表达式，其一阶累积Tracy－Widom分布函数表示为：

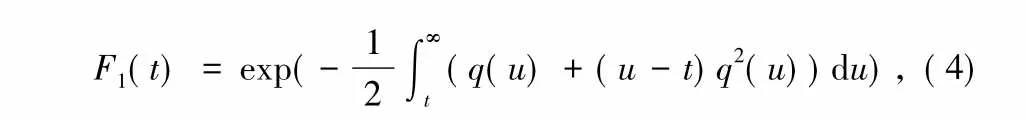
式中，q（u）是下面微分方程的解：

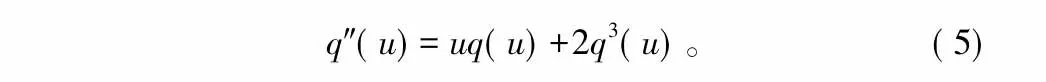
根据该分布函数求出判决门限随虚警概率变化的表达式，该算法克服了判决门限不固定的缺点。但是，MED算法同样存在当认知节点数和采样次数较小时，感知性能恶化的缺点；由于该分布函数只是近似表达式，当采样数较小时理论门限与统计门限误差较大，这会影响MED算法的确切性和可靠性。其中，MED算法的检验统计量为：

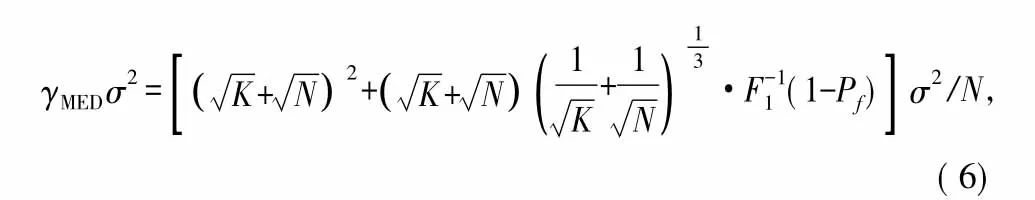
式中，K为认知用户个数，N为采样次数，由式子可以看出MED算法的判决门限与噪声功率有关，因此会受到噪声不确定性的影响。

2.2 最大最小特征值检测算法（MME）

该算法采用RMT理论对多个认知用户接收信号的采样协方差矩阵特征值分布特性进行分析，利用RMT中的极限渐进谱理论求出该协方差矩阵的最大和最小特征值的极限值，并将这2个极限的比值作为频谱检测的判决门限。基于极限理论可以得到如下表达式：

若TMME＝λmax/λmin＞γMME时，则判断主用户信号存在，否则判定不存在。

该算法无需任何主用户发射机信号的先验知识，而且克服了MED算法判决门限受噪声不确定性的影响。但是，由于该方法采用最大特征值和最小特征值的极限最为判决门限，造成不同感知情况下的判决门限始终不变，使其无法根据当前实际情况实时改变判决门限，这势必会大大影响系统的感知性能及其可靠性。

2.3 MMED检测算法

针对上述基于RMT理论的频谱感知算法的缺点，如参考文献［11］提出了一种新的合作感知算法（Maximum－Minimum Eigenvalue Detection，MMED）该算法对多认知用户采样协方差矩阵的最小特征值的概率分布特性进行研究，并获得了比采样协方差矩阵最大特征值概率分布更精确的最小特征值概率密度函数。根据该最小特征值的概率密度函数求得更精确的判决门限。最小特征值的概率密度函数服从二阶Tracy－Widom概率分布：

MMED算法的检验统计量只与采样次数N和认知用户数K以及二阶Tracy－Widom分布函数的反函数有关，与噪声无关。

最小特征值分布函数比最大特征值分布函数更加精确，因而使得MMED算法在认知节点较少、采样样本较小的情况下，亦能获得较好的感知性能。MMED算法无需主用户的任何先验知识及噪声功率等信息，并且其算法的复杂度几乎与MED算法和最大最小特征值之比算法相同。与基于最大特征值的频谱感知算法相比，MMED算法不仅具有感知性能更好以及对噪声不敏感等优点，而且在认知用户较少、样本较小的情况下，也可以获得较好的检测性能。

图6参数设置为：认知用户数为20，采样点数为3 000，MED－0dB和MED－3dB分别表示MED算法在噪声不确定性值为0 dB和3 dB时的检测性能。从仿真曲线可以看出MMED算法和最大与最小特征值比值的算法的ROC曲线不随噪声的波动而发生变化，而MED算法的检测性能对噪声比较敏感。当没有噪声波动时MED算法的漏检概率最低，其检测性能也最优，但当存在噪声波动且虚警概率增加到约0.55％时，MMED算法的性能最好。

图6 漏检概率随着虚警概率的变化曲线

图7参数设置为：认知用户数为20，虚警概率为0.05，其他参数保持不变。从仿真结果可以看出随着采样数的增加，3种算法的检测概率均有所增加，而且噪声对MMED算法和最大最小特征值之比算法的检测性能基本没有影响。当噪声不确定性为0 dB时，MED算法的检测性能最优，当噪声确定性为3 dB时，MED算法的检测性能最差，而且随着采样点数的增加，其检测性能增加不明显。

图7 检测概率随采样次数变化曲线

3 基于D－S理论的合作感知算法研究

D－S证据理论作为一种不确定的推理算法，是Dempster于1967年最初提出的［19］，后由它的学生Shafer对证据理论做出了进一步的研究，经过多年的发展已经可以形成由不知道引起的不确定性的较完整的理论体系。

在认知无线电系统中，由于信道的随机性，造成了认知节点对主用户信息感知的不确定性，使用DS融合规则来对各自感知节点的感知信息进行融合，如文献［20］提出的算法，改进了单节点算法中需要先验信息的缺点，该算法分为2个步骤进行判决，一是感知节点处的本地感知，二是中心控制融合节点的综合判决。融合中心采用D－S融合规则对各节点的感知信息进行融合，并根据一定的决策规则作出是否存在主用户信号的最终判决。D－S证据融合规则为：

式中，K＝∑m1（Ai）m2（Bj）反映了各个证据之间

Ai∩Bj＝A的冲突程度，系数1/（1－K）称为归一化因子。本算法的本地检测的结果对于假设H 0和H12种不同证据的支持程度即基本信任度分配函数设为mi（H0）和mi（H1）及感知节点对整个感知结果不确定信任度函数mi（T），其中，mi（H0）＋mi（H1）＋mi（T）＝1。融合中心收到来自各个节点的感知结果{mi（H0）、mi（H1）、mi（T）}之后根据式（11）得到感知的综合信任度{m（H0）、m（H1）、m（T）}，根据决策规则：

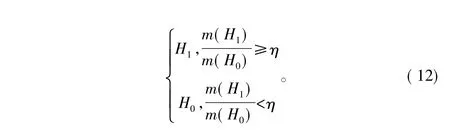
图8参数设置为：3个认知用户，信噪比分别为：－10 dB、－12 dB、－14 dB。从图8可以看出在不同信噪比条件下，采用D－S理论进行合并比其他2种合并在检测性能上均有大幅度提高。由上面2种情况可以得出结论，基于D－S证据理论的协作频谱感知算法与原有的频谱感知算法相比，其感知性能有了很大的提高。基于D－S理论的协作频谱感知不需要知道各个感知节点的信噪比、虚警概率，只需知道各个认知节点的感知结果就可以计算本次感知的信任度，融合中心传输结果时，只需要传送2个变量，节省开销。因此，D－S理论的频谱感知算法具有很高的利用价值。

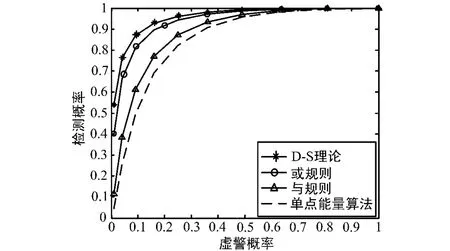
图8 4种算法在3种不同信噪比下的性能曲线

4 基于模糊理论的合作频谱感知算法

实际感知应用中，由于参与协作的感知的认知用户会受到一些不利因素的影响，如信道衰落、噪声不确定性及相邻节点阴影相关性等，导致融合中心最终结果的不确定性会很大，因此采用简单的融合方式不能充分反映用户的所有观测信息。而在实际环境中，针对D－S证据理论方法的缺点，文献［11］是基于模糊理论的合作频谱感知算法。模糊积分是可测函数关于模糊测度的积分，在融合中心采用模糊积分，本地检测算法采用能量算法，得到每个认知用户的检测统计量Yi，根据检测统计量构造可测函数fi（H0）和fi（H1），其中，fi（H0）表示第i个认知用户根据检验统计量得到本地检测结果为H0的隶属度，同时fi（H1）表示第i个认知用户根据检验统计量得到本地检测结果为H1的隶属度。由于检验统计量服从高斯分布，则选择正态形隶属函数进行可能性计算，其中a为调整因子。模糊积分的可测函数表达式为：

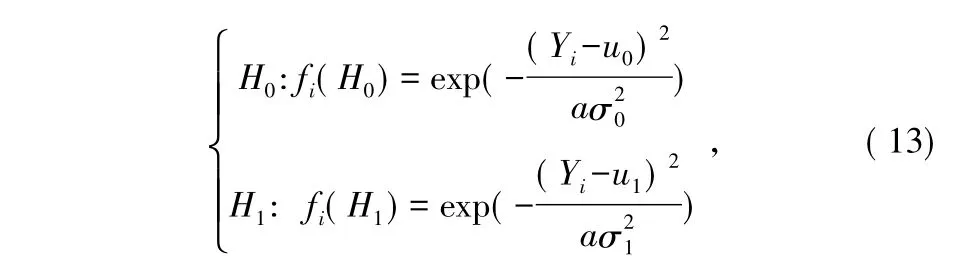
式中，a为调整因子取值为9，检验统计量Yi的出现率为99.7％，也就是表示几乎所有的Yi都能够分配到合理的隶属度，u0和u1，σ20和σ21分别为均值与方差。

对基于模糊积分的协作频谱感知算法所需的模糊测度多分类器数据融合的方法求解模糊测度。混淆矩阵和模糊测度表达式为：

各个认知用户将各自本地检测为有无主用户信号的隶属度传输到融合中心，融合中心将其与求得的模糊测度进行模糊积分处理，得到最终隶属度值，然后根据隶属度最大原则判决机制作出最终判决。

模糊积分表达式为：

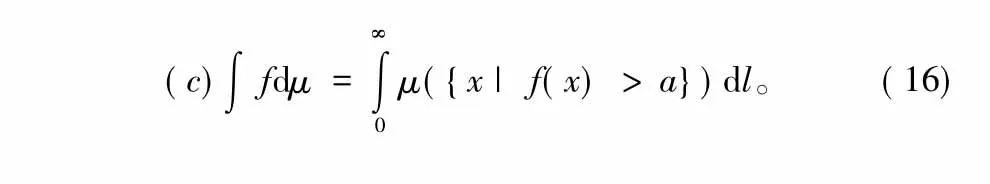
式中，（c）∫（.）f dμ是对（.）的模糊积分，μ是模糊测度值，X是给定的集合，x是集合内的元素，f是定义在X上的可测函数值。

图9为不同信噪比下检测性能比较。

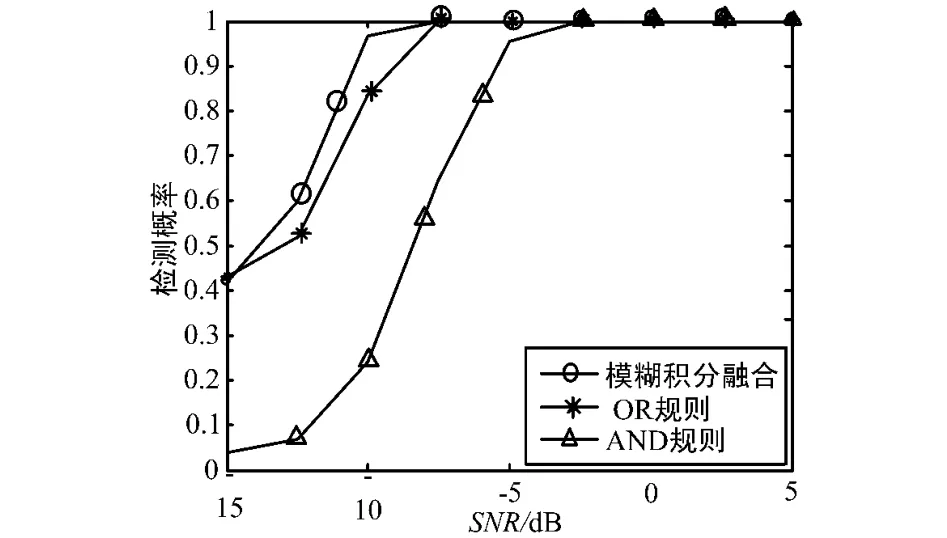
图9 不同信噪比下检测性能比较

图9参数设置为：在AWGN信道下，参与协作的认知用户本地感知用能量检测算法，取采样点数为300，主用户信号服从高斯分布，噪声也服从告诉分布。由图9可以看出，各融合方式的检测概率都随着信噪比的增加而增加，同时，在低信噪比的情况下，基于模糊积分协作频谱感知算法的检测概率相较于其他的检测算法都是最优的。但是当信噪比高于某一值后，各频谱感知算法的检测概率几乎都趋于1。可见，本方法可以有效地提高低信噪比情况下的检测概率，可以将此方法应用于低信噪比环境下的合作频谱感知中。

图10参数设置为：设信噪比均为－10 dB，由图可以看出，在相同信噪比条件下，基于模糊积分融合算法的检测概率高于“AND”和“OR”融合算法。由上述仿真结果可以得出，基于模糊积分的融合算法比硬判决的融合算法的性能好。

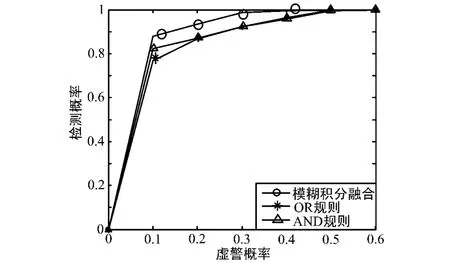
图10 信噪比相同时的检测概率比较

5 合作频谱感知算法未来研究方向及展望

上述的合作感知算法如AND和OR的融合策略的感知算法。这些关于频谱感知都是基于单输入单输入的情况。未来的移动通信必然会引入多天线技术，甚至可能在用户终端内置天线来获得更高的数据速率和更好的通信性能，这是移动通信发展的必然趋势。对多天线感知无线电的研究也不仅仅局限于提高检测性能，而是将重点放在提高感知网络的容量和吞吐量上。

节能问题一直是社会热点，然而频谱感知也不例外，在未来的研究中也会将通信开销问题作为重点研究方向。文献［16－18］所述的算法，指出了合作感知中通信开销的问题。该算法计算每个认知用户的信任度，对于信任度小于预先设定的信任度阈值的认知用户，不发送结果到融合中心。这样就使得占用信道的用户数明显减小，从而降低系统开销，并且检测性能也不会受到影响。未来频谱感知研究将重点放在节能、快速、准确的方向上。

［1］赵宝柱，邢志强，刘序明，等.基于最优计数准则的合作频谱感知算法［J］.传感器与微系统：2012，31（2）：48－51.

［2］卞荔，朱琦.基于数据融合的协作频谱感知算法［J］.南京邮电大学学报（自然科学版），2009，29（2）：73－78.

［3］杨铁军，司春丽.基于信任度加权的合作频谱感知算法［J］.计算机应用研究，2012，29（8）：3124－3127.

［4］段鹏，何明一，薛敏彪.基于信噪比软信息的协同频谱感知算法［J］.信号处理，2011，27（2）：183－188.

［5］余峰，宋春林，谈彩萍，等.基于信誉度的频谱感知数据融合算法［J］.通信技术，2012，45（5）：12－14.

［6］刘斌，杨俊安.基于数据融合的加权合作频谱感知技术［J］.电子技术应用，2008（12）：117－119，123.

［7］段鹏，何明一，薛敏彪.基于信噪比软信息的协同频谱感知算法［J］.信号处理，2011，27（2）：183－188.

［8］曹开田，杨震.一种新型的基于最大特征值的合作频谱感知算法［J］.电子与信息学报，2011，33（6）：1367－1372.

［9］曹开田，杨震，基于随机矩阵理论的DET合作频谱感知算法［J］.电子与信息学报，2010，32（1）：129－134.

［10］曹开田，杨震，基于最小特征值的合作频谱感知新算法［J］.仪器仪表学报，2011，32（4）：736－741.

［11］曹开田，王尚.基于RMT的合作频谱感知新算法及其性能分析［J］.计算机应用研究，2011，28（7）：2640－2642，2646.

［12］肖淑艳，孙茜，衡芹，等.基于D－S理论的认知无线电频谱感知算法［J］.计算机工程与应用，2011，47（33）：91－93.

［13］王苗苗，李世银，肖淑艳，等.基于改进D－S证据理论的认知无线电频谱感知算法［J］.电讯技术，2012，52（8）：1303－1307.

［14］Liu Wei－dong Liu，Lv Tie－jun，XIA Jin－huan，et al.An Optimal Cooperative Spectrum Sensing Scheme Based on Fuzzy Integral Theory in Cognitive Radio Networks［C］∥Personal，Indoor and Mobile Radio Communications，2009 IEEE 20th International Symposium on Digital Object Identifier：1019－1023.

［15］杨黎，王晓湘，赵堃.多天线感知无线电中的协作频谱感知算法［J］.电子与信息学报，2009，31（10）：2338－2342.

［16］Chen H，Wu W，Xie L.Cooperative Spectrum Sensing Scheme with Light Communication Overhead in Cognitive Radio Networks［C］∥Proc.Of IEEE PIMRC 2010，2010：1539－1543.

［17］Yao J，Leung K，Li V O K.A Random Censoring Scheme for Cooperative Spectrum Sensing［C］∥Proc.of IEEE GLOBECOM 2011，2011：1－5.

［18］Zhang Nan－nan，Chen Hui－fang，Xie Lei.A Communication－overhead－aware Cooperative Spectrum Sensing Scheme in Cognitive Radio Networks［C］∥Proc.of IEEE GLOBECOM 2012：351－356.

［19］Dempster A P.Upper and Lower Probabilities Induced by a Multivalued Mapping［J］.The Annals of Mathematical Statistics，1967，38（2）：325－339.

［20］Zhang Shi－bing，Yang Jiao－jiao，Guo Li－li.Eigenvaluebased Cooperative Spectrum Sensing algorithm［C］∥2012 Second International Conference on Instrumentation ＆Measurement，Computer，Communication and Control，2012：375－378.

Review of Cooperative Spectrum Sensing Algorithm for Cognitive Radio

BAO Zhi－qiang，SHIYuan－yuan
（School of Communication and Information Engineering，Xi’an University of Posts and Telecommunications，Xi’an Shaanxi710061，China）

Spectrum sensing is a prerequisite for the realization of cognitive radio function，and also a hot research topic in cognitive radio field.In recent years，lots of methods have been proposed for spectrum sensing，especially the cooperative spectrum sensing algorithms，which are attracting more and more attention.This paper summarizes the latest research progress in cooperative spectrum sensing technology，such as simple linear weighted sensingmethods，nonlinear weighted algorithms and cooperative sensing algorithms with multiple antennas.The detection performance of variousmethods is compared through simulations，and the challenges for the future spectrum sensing are given.

cognitive radio；cooperative sensing；information fusion；detection performance

TN92

A

1003－3114（2015）04－24－7

10.3969/j.issn.1003－3114.2015.04.06

包志强，史园园.认知无线电合作频谱感知算法研究［J］.无线电通信技术，2015，41（4）：24－30.

2015－03－02

国家自然科学基金项目（61271276）；陕西省自然科学基金项目（2012JQ8011）；陕西省教育厅自然科学研究项目（11JK0925）

包志强（1978—），男，副教授，博士，主要研究方向：阵列信号处理和频谱感知技术。史园园（1988—），女，硕士研究生，主要研究方向：认知无线电频谱感知技术研究。