Boussinesq-Burgers方程的达布变换及其计算机机械化实现
2015-01-10李拔萃
李拔萃
(中共辽宁省抚顺市委党校 公共管理教研室,辽宁 抚顺 113006)
Boussinesq-Burgers方程的达布变换及其计算机机械化实现
李拔萃
(中共辽宁省抚顺市委党校 公共管理教研室,辽宁 抚顺 113006)
Boussinesq-Burgers方程是孤立子理论中的一个重要的方程,在物理学中有许多应用。本文构造出Boussinesq-Burgers方程的一个新的达布变换。利用这个达布变换,在符号计算软件Maple的帮助下,可以得到该方程新的孤子解。
Boussinesq-Burgers方程;达布变换;符号计算软件;孤子解
孤立子理论在自然科学的众多领域中扮演着非常重要的角色。一方面它在量子场论、粒子物理、凝聚态物理、流体物理、等离子体物理和非线性光学等物理学的各个分支及数学、生物学、化学、通信等各自然科学领域得到了广泛的应用;另一方面它极大地促进了一些传统数学理论的发展,为非线性偏微分方程提供了求解显示解的方法。孤立子理论中构造非线性偏微分方程精确解的方法有齐次平衡法、Tanh函数法、反散射方法、双线性变换法、李群法和达布变换法等等[1-6]。其中达布变换法是寻找孤子解的一种有力工具[7-9]。本文考虑重要的Boussinesq-Burgers方程,构造出一个新的达布变换,利用这个达布变换在符号计算软件Maple的帮助下以获得Boussinesq- Burgers方程新的孤子解。
2 Boussinesq-Burgers方程的达布变换
Boussinesq-Burgers方程
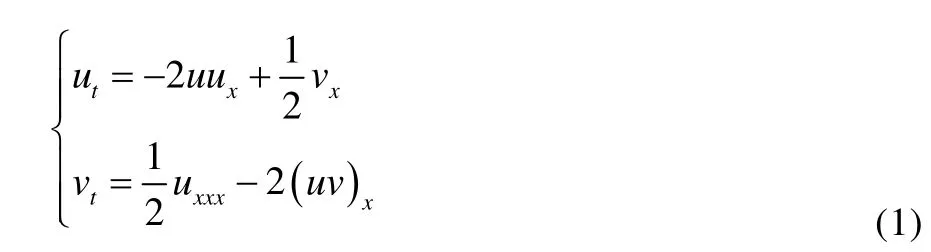
考虑如下谱问题的Lax对

其中u和v是两个位势,λ是谱参数。



3 Boussinesq Burgers方程的孤立子解
已证明的定理表明变换(4)式把旧的谱问题(2)-(3)式变换成了相同的谱问题(7)-(8)式。因此若(u,v)是Boussinesq-Burgers方程的一组解,则由变换(15)式确定的也是Boussinesq-Burgers方程的解。
现在取Boussinesq-Burgers方程(1)的一组平凡解u=0,v=-1作为种子代入到Lax对(2)-(3)式中,可求得其两个基本解

再由(10)式可以求得a,c,d。最后根据(15)式得到Boussinesq-Burgers方程的一组新的精确解

4 总结
本文通过构造Boussinesq-Burgers方程一个新的达布变换,并利用这个达布变换在符号计算软件Maple的帮助下获得了该方程的新的孤子解。这些解不仅是利用其它方法所得不到的,也是其它文献中所没有的,而且有重要的物理意义,可以合理地解释相关的自然现象,很好地描述各种物理现象,比如振动、传播波等。
[1] 古超豪,胡和生,周子翔.孤立子理论的达布变换及其几何应用[M].上海:上海科学技术出版社,1999:55-59.
[2] 李志斌.非线性数学物理方程的行波解[M].北京:科学出版社,2007:2-7.
[3] 范恩贵.可积系统与计算机代数[M].北京:科学出版社,2004: 105-107.
[4] Yufeng Zhang, Zhonglong Zhao, Guangming Wang. On generating linear and nonlinear integrable systems with variable coefficients[J]. Applied Mathematics and Computation, 2014, 244 (2) 672–682.
[5] ZHANG Yu-Feng, Hon-Wah Tam. Generation of Nonlinear Evolution Equations by Reductions of the Self-Dual Yang–Mills Equations[J]. Commun. Theor. Phys., 2014, 61 (2): 203-206.
[6] Bacui Li, Yufeng Zhang. Explicit and exact travelling wave solutions for Konopelchenko-Dubrovsky equation[J]. Chaos, Solitons and Fractals, 2008, 38(4): 1202-1208.
[7] Fan E G. Solving Kadomtsev-Petviashvili Equation via a New Decomposition and Darboux Transformation[J]. Commun. Theor. Phys., 2010, 37(2): 145-148.
[8] Li Y S, Zhang J E. Darboux transformations of classical Boussinesq system and its multi-soliton solutions[J]. Physics Letters A, 2010, 284(3): 253-258.
[9] Yan Z Y, Zhang H Q. New Auto-Darboux Transformation and Explicit Analytic Solutions for the Generalized KdV Equation with External Force Term[J]. Journal of Mathematical Research & Exposition, 2001, 21(1): 323-328.
(责任编辑、校对:赵光峰)
Darboux Transformation for the Boussinesq-Burgers Equation and Computerized Mechanization
LI Ba-cui
(Department of Public Management, Party School of CPC Fushun Municipal Committee, Fushun 113006, China)
Boussinesq-Burgers equation is a significant equation in soliton theory. There are many applications in physics. In this paper, we construct a new Darboux transformation for the Boussinesq-Burgers equation. By means of this Darboux transformation and with the aid of symbolic computation software, many new solitary solutions are obtained.
Boussinesq-Burgers equation; Darboux transformation; symbolic computation software; solitary solution
O175.29
A
1009-9115(2015)02-0010-03
10.3969/j.issn.1009-9115.2015.02.003
2015-03-05
李拔萃(1983-),女,辽宁抚顺人,硕士,讲师,研究方向为孤立子理论 数学机械化。
