广义弱亚正规算子的Riesz幂等元
2015-01-10杨桦
杨 桦
(安阳工学院 数理学院,河南 安阳 455000)
广义弱亚正规算子的Riesz幂等元
杨 桦
(安阳工学院 数理学院,河南 安阳 455000)
研究了广义弱亚正规算子T的Riesz幂等元Eλ和T的广义Aluthge变换t的Riesz幂等元λ的性质,其中λ∈isoσ(T)。证明了EλH=λH,Eλ是自伴算子,和EλH=ker(T-λ)=ker(T -λ)*。
广义弱亚正规算子;Riesz幂等元;广义Aluthge变换
1 引言
近年来许多学者对p-亚正规算子,弱亚正规算子,p-弱亚正规算子、log-弱亚正规算子及A类算子进行了研究[1-6],并已有了大量的成果。如Ch和Tanahashi[1]得到:若T是亚正规算子,则Eλ是自伴的,并且

而且他们证出,若T是p-亚正规算子或log-亚正规算子时,上述结论也成立;Han Young Min等[2]证出上述结论对弱亚正规算子也成立;杨桦等[3,4]证出上述结论对p-弱亚正规算子及log-弱亚正规算子也成立。2011年,杨桦等[7]引进了广义弱亚正规算子的定义,并得到许多重要的结论,如:
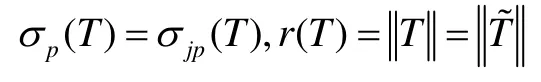
等。本文在以上文献的基础上,继续讨论广义弱亚正规算子的性质,并证出了广义弱亚正规算子的Riesz幂等元的一些结论。
我们先给出文中要用到的一些基本定义和引理。
设H是Hilbert空间,B( H)表示H上有界线性算子的全体。设T∈B( H),isoσ(T)表示σ(T)中的全体孤立点。若λ∈isoσ(T),则与λ有关的T的Riesz幂等元
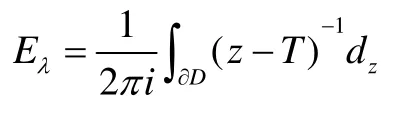
其中D是Cσ(T)中的开圆盘且λ∈D。
我们已经知道Eλ满足

定义1[7]设T∈B( H),若(T*T)p≥(TT*)p,其中p>0,我们称T是p-亚正规算子。特别地,当p=1时称为亚正规算子及当p=1/2时称为半亚正规算子。T=U| T|是T的极分解,定义T的广义Aluthge变换

则称T是弱亚正规算子。若

其中0 引理1[3]若T是p-弱亚正规算子,则 定理1 T是广义弱亚正规算子,若~tT具有性质 从而Eλ是自伴的。 如果∀λ∈isoσ(T)都有ℜ(T-)λ是闭的,则称T是reguloid。 推论2 若T是广义弱亚正规算子,则T是reguloid。 证明 ∀λ∈isoσ(T),则 因为T是广义弱亚正规算子,那么由定理4知 又因为T2-λ是可逆的,所以ℜ(T-)λ是闭的,即T是reguloid。 [2] Han Young Min, Lee Jun IK, Wang Derming. Riesz idempotent and Weyl’s Theorem for w-hyponormal operators [J]. Integral Equations and Operator Theory, 2005, 53: 51-60. [3] 杨桦,常欢.p-弱亚正规算子的Riesz幂等元和Weyl定理[J].黔南民族师范学院学报,2008,28(6):30-33. [4] 杨桦,卢凤梅.log-弱亚正规算子的Riesz幂等元和Weyl定理[J].唐山师范学院学报,2010,32(5):22-25. [5] 杨桦,常欢,吉国兴.p-弱亚正规算子的正规性[J].山东大学学报(理学版),2013,48(9):68-72. [6] 高福根,李晓春.1个初等算子和广义Weyl定理[J].河南师范大学学报,2013,41(5):151-151. [7] 杨桦,李艳军.广义弱亚正规算子[J].唐山师范学院学报, 2011,33(5):1-3. [8] Riesz F, Sz-Nagy B. Functional Analysis[M]. New York: Frederick Ungar, 1955: 424-424. (责任编辑、校对:赵光峰) Riesz Idempotent for the Generalized W-Hyponormal Operators YANG Hua (Science Faculty, Anyang Institute of Technology, Anyang 455000, China) Some characterizations of Riesz idempotent Eλandλ, with respect to ∀λ∈isoσ(T), of T and, respetively are given. It shows theEλH=λH. Consequently, Eλis self-adjiont andEλH=ker(T-λ)=ker(T-λ)*. the generalized w-hyponormal operator; Riesz idempotent; the generalized Aluthge transformation O177.1 A 1009-9115(2015)02-0006-04 10.3969/j.issn.1009-9115.2015.02.002 2014-09-22 杨桦(1982-),女,河南周口人,硕士,讲师,研究方向为算子代数。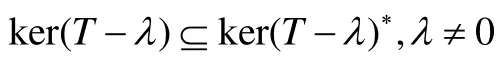
2 Riesz定理







