热膜式气流量传感器指数过渡分段拟合方法

彭 丹，杨 磊，杨家强

（浙江大学电气工程学院，浙江杭州310027）

热膜式气流量传感器指数过渡分段拟合方法

彭 丹，杨 磊，杨家强

（浙江大学电气工程学院，浙江杭州310027）

为了提高应用于高速列车通气管道监测列车运行状态的热膜式气体流量传感器输出特性的曲线拟合精度，在多项式拟合和分段拟合的基础上，提出指数过渡分段拟合方法.该方法对气体流量和输出电压的关系进行分段拟合，人为选择一个分界点，利用2组原始数据得到2条拟合曲线，2条拟合曲线相交得到一个交点，利用交点的前一个原始数据点和后一个原始数据点构成过渡区间，使用指数函数修正交点附近的过渡区间，解决了分段拟合不平滑的缺陷，实现了曲线间的光滑过渡.对提出的拟合方法进行实验验证，给出并比较了多项式拟合、分段拟合和指数过渡分段拟合的结果.结果表明，提出的指数过渡分段拟合方法具有很高的拟合精度，拟合误差不大于1.5％，方法简单、可靠.

气体流量传感器；曲线拟合；多项式；分段；自然相交；指数曲线过渡

热式气体流量传感器是在早期热线风速仪的基础上发展来的一种直接式气体质量流量测量仪器，具有压损低、流量范围大、精确度高、重复性好、无可动部件以及可用于极低速微小气流测量等优点，已经广泛应用到高速火车、航空航天、汽车工业、医疗设备、能源测量以及天然气管道运输等工业领域[1-2].气体流量传感器在实际应用之前须对它的输出特性进行标定，得到输出量电压或者电流与气体流量之间的关系.传感器输出特性的标定方法主要有如下2种.1）通过理论推导得到传感器的输出与气体流量、温度、压强等变量之间的函数关系，再通过测定上述相关变量确定输出特性，但是由于不同传感器内部电路结构的不同，函数关系需要单独推导；2）直接测量一系列不同气体流量下传感器的对应输出数据，对测得的数据进行曲线拟合，因此测量数据的精度与拟合方法的选择直接关系最终输出特性的准确性[3].

国内外许多学者研究了指数拟合、多项式拟合等不同数据曲线拟合方法对标定传感器输出特性的影响.蔡春丽等[4]采用指数函数对测得的气体体积流量与传感器输出电压进行曲线拟合，拟合曲线光滑，曲线单调性和延展性与测量数据显示的趋势相符.该方法在大流量区间具有很小的拟合误差，但是在微小流量区间的拟合结果不太理想，拟合误差较大.赵伟国等[5]使用六次高阶多项式进行曲线拟合，改善了文献[4]中指数函数在小流量区间拟合误差大的缺点，但是在大流量区间的拟合误差较大，尤其是对原始流量测量数据范围外的拟合结果不太理想.Vapnik等[6-9]针对拟合物理量之间关系的非线性性，将神经网络、支持向量机学习器等基于数理统计的方法引入拟合过程，逐渐形成了一套比较完整的数据处理和拟合系统，使得拟合过程更具系统性、科学性.Vapnik等[6-9]指出这些智能方法的整个过程过于复杂化，会导致实验系统的可靠性降低，不利于实际应用；这些方法数学模型的参数所代表的物理意义不够明确，典型的例子如支持向量机方法中的感知器核函数参数β.

针对上述各种拟合方法的不足，本文基于热式流量传感器在不同气体流速范围内热量传递因素之间的差异，提出指数过渡分段拟合方法.对各段流量区间内的流量和电压数据进行单独拟合，通过分段曲线相交得到精确的衔接点，采用指数函数修正了衔接点附近的过渡曲线，从而实现曲线之间的平滑连接.拟合结果表明，指数过渡分段拟合方法具有最高的拟合精度，在每段流量区间内的拟合误差都不高于1.5％，方法简单、可靠.

1 热膜式气体流量传感器的基本原理

1.1 流量测量原理

热式气体流量传感器是一种基于气体热传递原理的传感器.当气体流过加热元件时，会导致元件表面温度的变化，该变化量与气体的流速和温度有关[10-13].工作原理如图1所示.热传递主要有强迫对流传热、自然对流传热、导热传热和辐射传热4种方式，热式气体流量传感器气流与加热元件之间的热传递以强迫对流传热为主.

图1中，2个热敏电阻RS和RH分别位于惠思顿电桥的两臂，并置于气流管道中，分别用于测量气体的流速和温度[1，13-14].

根据传热学原理可知，提供给加热元件的电功率与气流通过强迫对流换热带走的热量相等，可得

式中：IH为加热元件的电流，RH为加热元件电阻，h为表面传热系数，AS为加热元件表面积，TH为加热元件的表面温度，Tr为气流的温度.式（1）中h AS与气体流量有关，可以表示为

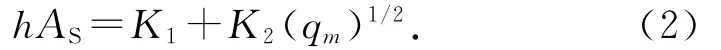
式中：K1和K2为经验常数，可以通过实验测定；qm为气流的质量流量.将式（2）代入式（1），可得

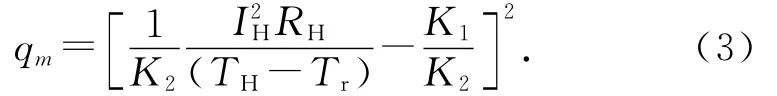
由式（3）可以得出，当Tr一定时，qm是IH和TH的函数.若保持其中一个变量固定，则可以得到qm与另一个变量的函数关系.若保持TH一定，则可以根据测量IH得到qm.这种测量方式称为气体流量传感器的恒温工作方式.

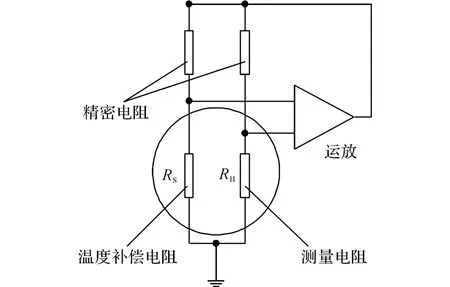
图1 热式流量传感器的原理图Fig.1 Schematic diagram of gas flow sensor

1.2 测量电路

气体流量传感器采用恒温方式进行测量，测量电路如图2所示.

图2 气体流量传感器测量电路Fig.2 Measuring circuit of gas flow sensor

图2中，温度测量铂电阻RH和流速测量铂电阻RS集成在同一个热膜探头上，热膜探头的型号为FS5.该热膜探头与精密电阻R1、R2、R3、R4共同构成惠思顿电桥两臂，通过自动校正法实现对气流测量的温度补偿.在不同气体流速下，测量电路输出的对应电压信号为U1，U1的输出范围为2.7～6.0 V.

2 指数曲线过渡分段拟合方法

在气体流量的测量过程中，气体流量与传感器测量电阻之间的热量传递以强迫对流传热为主，在处理时通常忽略自然对流传热、导热传热和辐射传热的热传递方式对气体流量测量的影响.实际上，当气体流速较小时，在这段流量范围内测量电路输出电压受气体流量变化的影响不很明显，此时相对于强迫对流传热，自然对流传热、导热传热及辐射传热不能忽略；当气体流速较大时，由式（3）可知，此时输出电压受气体流量的影响较大，其他传热方式可以忽略.在不同流量范围内，气体流量与电压输出数据之间的关系应当分段单独拟合，从而减小最终拟合曲线与实际特性曲线之间的拟合误差.

2.1 分段拟合方法的优点和存在的问题

分段曲线拟合具有较多的优点，尤其在测得数据的变化趋势具有较大变化时，对原始数据进行合理分段拟合可以明显地降低拟合误差.分段拟合的主要优点如下.

1）分段拟合可以提高拟合精度.对数据点进行分段处理后，各段范围内点与点之间的变化将显得更平缓一致，有利于减小拟合误差.

2）分段拟合可以简化每段曲线的拟合方程.对数据点进行分段处理后，每一段的拟合曲线更加趋于线性化，能够降低曲线拟合的最高次数.

3）分段拟合能够避免在数据过渡区间的拟合结果出现明显错误.当一组测量数据出现如图3所示的变化趋势时，曲线B段快速上升，若直接对整段区间进行曲线拟合，则将不可避免地造成拟合曲线在A、B之间的过渡区间出现低于A的部分.这是由于数据点的变化趋势以及全段拟合函数不可突变2个因素所决定的，与拟合曲线函数的类型（多项式、指数等）选择无关.该拟合结果与传感器数据单调递增的变化趋势不相符，采用分段拟合可以有效地避免这一缺陷.

分段拟合虽然有着上述的优点，但是在分段过程中会出现一些明显的问题，其中最主要的是各段拟合曲线在过渡点的衔接问题.

如图4（a）、（b）所示分别为曲线分段拟合常见的过渡点衔接示意图.其中点划线表示在原始测量数据中人为选定的分界点，分界点两边的曲线由分段之后的数据分别拟合得到，qV-A表示前段曲线在分界点处的拟合值，qV-B表示后段曲线在分界点处的拟合值.

图4（a）所示的拟合结果会造成在某段流量范围内气体流量值偏大的情况.图4（b）所示的拟合结果会造成气体流量值在某点发生突变的情况.

该分界点分段曲线拟合方法在对精度要求不高的场合中，若分界点处拟合误差≤ε，即分界点处拟合误差小于设定偏差ε，则一般认为拟合结果可以接受；否则，需要确定新的分界点，重新分段拟合.

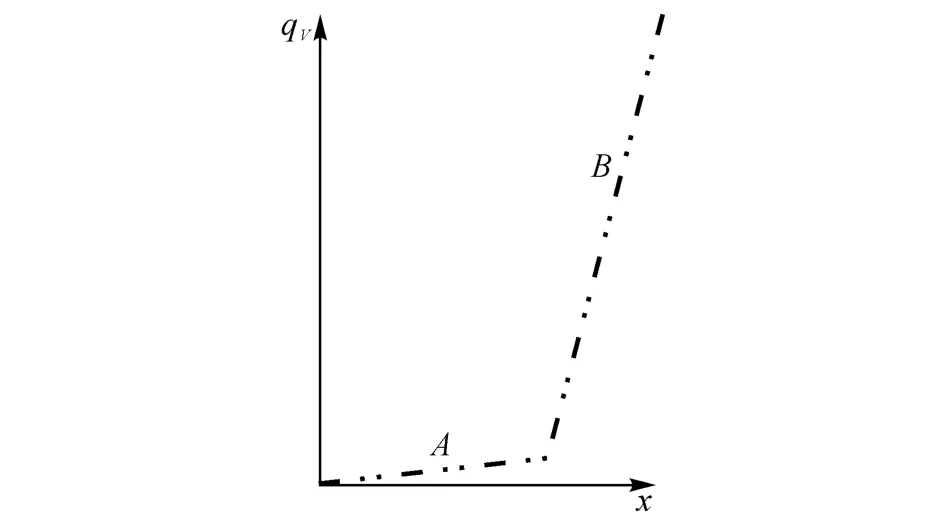
图3 数据分布变化趋势示意图Fig.3 Distribution of measured data

一般取ε为分界点处气体流量与传感器测量误差的乘积，表达式为

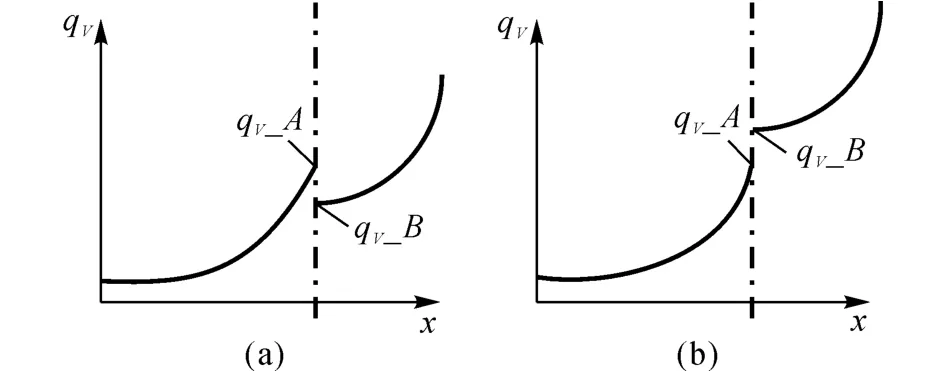
图4 分段拟合常见的衔接示意图Fig.4 Two normal connection problems of piecewise fitting

式中：qV为分界点处的实测值，e为气流传感器所允许的误差.鉴于工程应用上要求成品传感器的测量误差小于5％，在要求不高的场合，可以取ε= qV×5％.

分界点分段曲线拟合方法是一种误差可控的曲线拟合方法，在一定程度上优于传统的多项式拟合，但是在各段曲线衔接处往往存在断点，拟合曲线不光滑，结果不能令人十分满意，需要进行修正.

2.2 分段拟合数学模型

在分界点分段拟合中，分界点是人为地从原始测量数据点中选取的一个最接近曲线变化趋势的转折点，却不一定是真正意义上的转折点.尝试采用一种自然相交分段拟合的方法，找到真正意义上的转折点，并解决分界点分段拟合不平滑的缺陷，实现分界点分段拟合方法曲线的光滑过渡.

为了实现拟合曲线的自然相交，自然相交分段拟合方法的基本步骤可以分为如下2步.

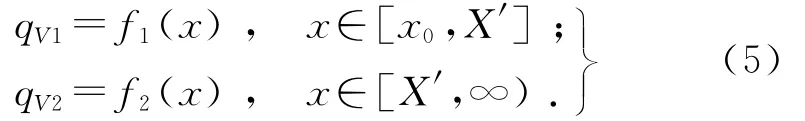
2）在x∈[x0，∞）上联立式（5）的2个表达式求解，得到交点（X，qV）.其中，x0表示气体流量为0时测得的电压值.这些数据点和拟合曲线的位置关系示意图如图5所示.

2.3 指数曲线过渡方法拟合表达式

在上述传统的分段拟合方法基础上，提出指数曲线过渡改进措施，使得整个分段拟合方法更加完善，拟合精度也有所提高.

由图5可知，上述步骤虽然解决了分段拟合不连续的问题，但在分界点处衔接不够平滑.为了克服该缺点，基于自然相交分段拟合的拟合结果对拟合方法进行改进.当x∈[x0，X＇]时，采用qV1=f1（x）计算气流量；当x∈[x1，∞）时，采用qV2=f2（x）计算气流量，其中x1指人为分界点后面的一个实测数据点的电压.当x∈[X＇，x1）时，采用过渡曲线来改善衔接点处的连接.为了方便叙述，将曲线qV1= f1（x）在x=X＇处对应的数值点（X＇，f1（X＇））称为A点，将曲线qV2=f2（x）在x=x1处对应的数值点（x1，f2（x1））称为B点.

图5 数据点和拟合曲线的位置关系示意图Fig.5 Position relation between data points and fitting curves

自然系统状态过渡多以指数形式进行，采用指数表达式来描述过渡曲线，则过渡曲线的表达式为

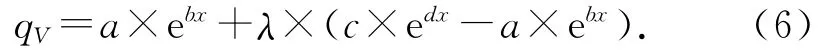
式中：λ为与x有关的系数，当x从x=X＇逐渐增加到x=x1时，λ从0逐渐增加到1.

记指数项y1=a×ebx，且它满足以下2个条件.

1）在x=X＇处的拟合值与A点重合；

2）在x=X＇处的导数与式qV1=f1（x）在A点的导数相等，可得

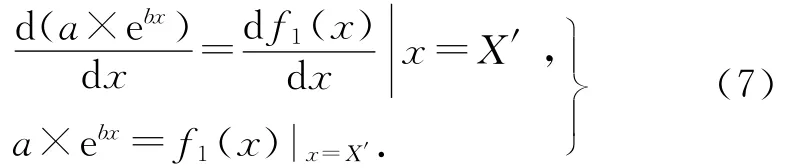
记指数项y2=c×edx，且它满足以下2个条件.

1）在x=x1处的拟合值与B点重合；

2）在x=x1处的导数与qV2=f2（x）在B点的导数相等，可得

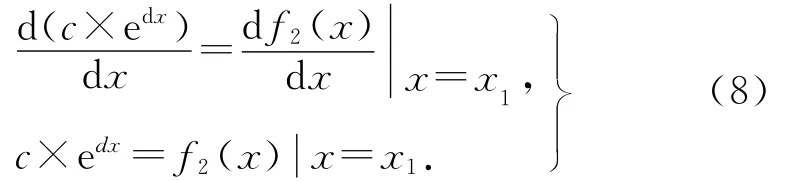
y1、y2都仅仅是一项指数项表达式，也可以增加指数项项数，使y1和y2成为多个指数项相加的形式，即

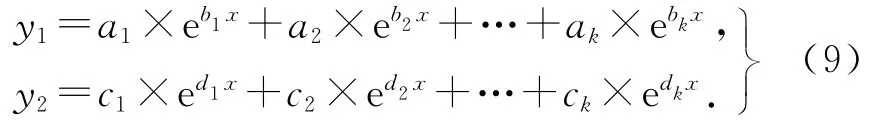
通过令y1在x=X＇处，y2在x=x1处的高阶导数与qV1=f1（x）在A点、qV2=f2（x）在B点的高阶导数相等，得到式（9）各项系数a1，a2，…，ak，b1，b2，…，bk，c1，c2，…，ck，d1，d2，…，dk，即

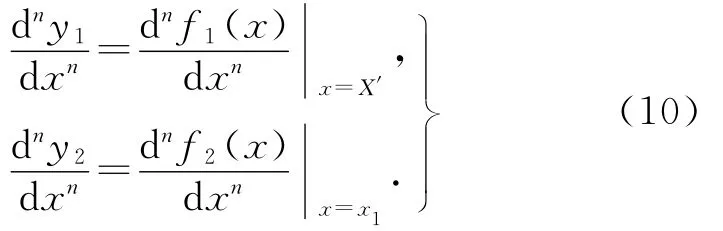
式中：n的取值依次为0，1，2，…，2k-1.考虑到实际工程的需要，y1和y2均取一项指数项.整段曲线的拟合表达式为

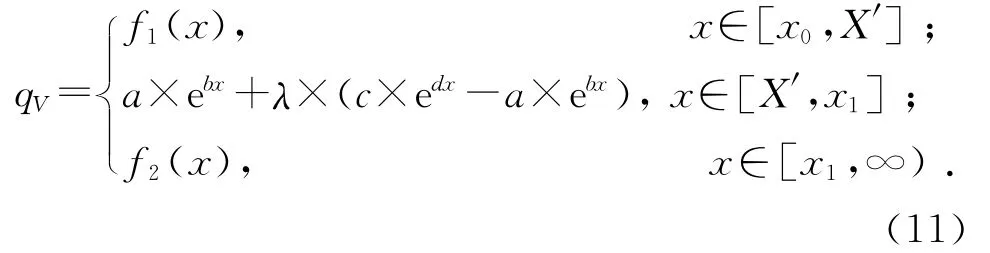
3 实验结果及分析

为了对提出的指数过渡分段拟合方法进行拟合精度的检验，设计了一种基于FS5探头的热膜式气体流量传感器，测量得到气体流量与对应的输出电压的数据.对这些数据点分别进行多项式拟合、传统分段拟合和指数曲线过渡分段拟合方法对比实验研究，给出这3种拟合方法的拟合精度.

如图6所示为本实验所采用的标定装置示意图，主要由风源、阀门、标准流量计、待校流量计及数据处理系统构成.图中，U为待测流量计5的DSP采样电压，由图2的测量电路输出电压U1分压得到.U和标准流量计4所测得的气流量共同构成了原始拟合数据.

实验过程如下：打开鼓风机1和截止阀2；旋转调节阀3，调节管道的气流量，使气体以一定的流量流动；待标准流量计4所测气流量、待校流量计5所采样的电压稳定后，记录上述数据.

图6 标定装置框图Fig.6 Diagram of calibration device

测得的一组实验结果数据如下：

x=[0.705，0.801，0.898，0.997，1.089，1.188，1.274，1.336，1.396，1.454，1.506，1.560，1.614，1.629]，qV=[0，0.32，0.93，1.92，3.7，9.2，14.2，20.2，26.7，33.7，39.5，44.6，49.4，53.9].

其中，x为传感器的输出电压.如图7所示为上述实测数据的二维描点.

图7 实测数据二维描点Fig.7 Measured data in rectangular coordinate

由图7可得，实测数据点的走势大致可以分为2部分，分界点x=1.089.前面部分为低流量段，包含前面5个数据点，即x=[0.705，0.801，0.898，0.997，1.089]；后面部分为高流量段，包括后面10个数据点，即x=[1.089，1.188，1.274，1.336，1.396，1.454，1.506，1.560，1.614，1.629].

3.1 多项式拟合曲线及分析

对以上数据点进行多项式拟合，得到二次、三次以及四次拟合曲线，如图8～10所示.

由图8～10的多项式拟合曲线可知，二次和三次多项式的拟合结果相对精确，当多项式次数达到四次时，拟合曲线在x∈（1.629，∞）区间的延展性和预测性变差.此外，二次多项式拟合在气体流量很低时，出现了曲线递减的情况，造成部分气体流量拟合结果小于0的缺陷，如图8的局部放大图.这一问题在三次多项式拟合中也存在.

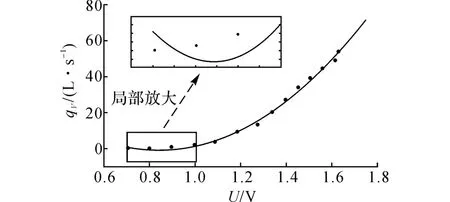
图8 二次多项式拟合曲线Fig.8 Fitting curve of quadratic polynomial

图9 三次多项式拟合曲线Fig.9 Fitting curve of cubic polynomial

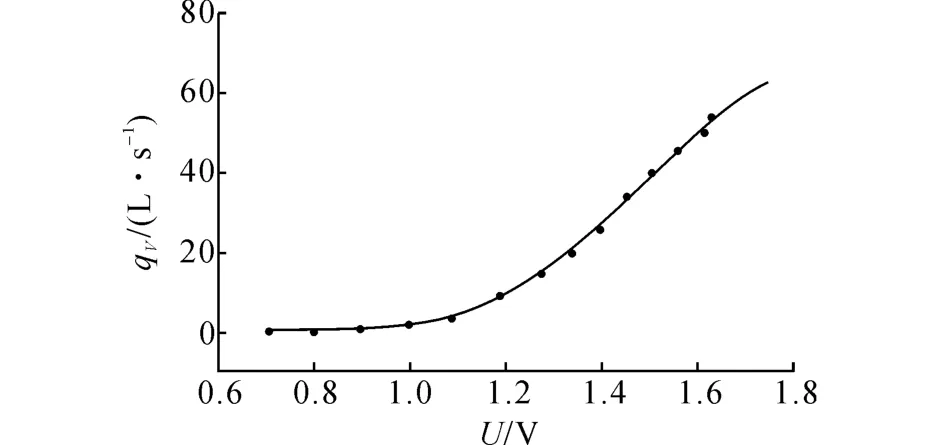
图10 四次多项式拟合曲线Fig.10 Fitting curve of quartic polynomial

3.2 分段拟合曲线及分析

对测量的数据不作任何处理，直接进行分界点分段曲线拟合，可有如下4种拟合方式.1）将“分界点”仅作为第一段拟合曲线的拟合点；2）将“分界点”同时作为两段拟合曲线的拟合点；3）将“分界点”不作为任何拟合曲线的拟合点；4）将“分界点”仅作为第二段拟合曲线的拟合点.采用前3种分段拟合方式具有相似的拟合结果，可以用图11表示.

由图11可知，分界点分段曲线拟合的前3种拟合方式都存在在衔接点处不连续的问题，与图4（a）的情况相同，拟合结果不够理想.

如图12所示为采用分界点分段拟合第4种拟合方式所得到的分段拟合结果.可见，拟合方式4）的结果相对精确，虽然衔接点处存在不连续的问题，但在衔接点处没有明显的偏差.

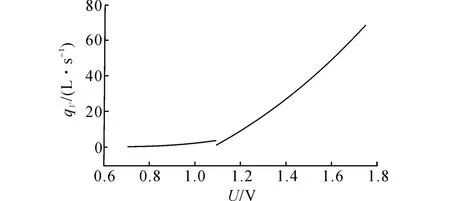
图11 拟合方式1）～3）的分段拟合曲线Fig.11 Piecewise fitting curve of model1）-3）

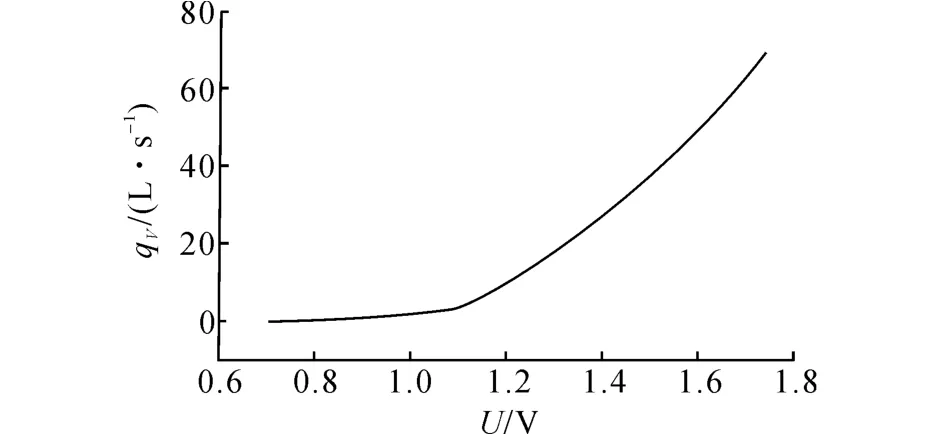
图12 拟合方式4）的分段拟合曲线Fig.12 Piecewise fitting curve of model 4）

经实际计算得到第一段曲线在“分界点”x=1.089处所对应的气流量qV-A为3.125 6L/s，第二段曲线在“分界点”x=1.089处所对应的气流量qV-B为3.1024L/s，两者差为0.0232L/s.前者略大于后者，但考虑到气流传感器所允许的误差ε=3.2×5％=0.185＞0.0232，可以认为在误差的允许范围之内.

3.3 指数过渡分段拟合曲线及分析

对测量的数据不作任何处理，采用上述的自然相交分段曲线法进行分段曲线拟合.对前部分数据点x=[0.705，0.801，0.898，0.997，1.089]、qV= [0，0.32，0.93，1.92，3.7]进行二次多项式拟合，可得

对后部分数据点x=[1.089，1.188，1.274，1.336，1.396，1.454，1.506，1.560，1.614，1.629]，qV=[3.7，9.2，14.2，20.2，26.7，33.7，39.5，44.6，49.4，53.9]进行二次多项式拟合，可得

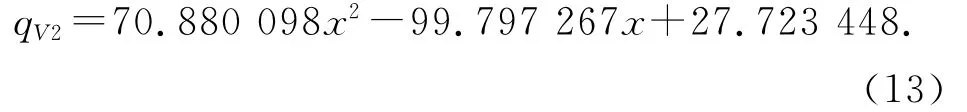
联立式（12）、（13），求得2条曲线的交点坐标为（1.103 64，3.916 87），即当x∈[0.705，1.103 64] 时，采用式（12）计算气流量；当x∈（1.103 64，∞）时，采用式（13）计算气流量，因此，最终的拟合曲线表达式为

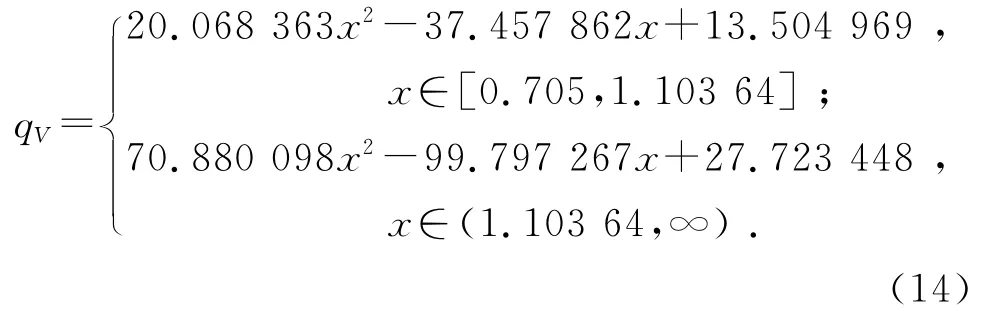
如图13所示为由式（14）所得的分段拟合曲线.由图13可知，两段拟合曲线在衔接处不够平滑.利用提出的指数过渡曲线方法可以对衔接处进行修正，由式（8）、（9）求得指数项表达式如下：

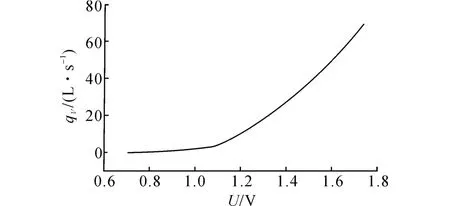
图13 无过渡曲线分段拟合曲线Fig.13 Piecewise fitting curve without transition curve

在式（11）表示的过渡曲线表达式中，λ为与x有关的系数，当x从x=X＇逐渐增加到x=x1时，λ 从0逐渐增加到1.

取λ的表达式为

将式（15）、（16）代入式（6），可得实测数据的过渡曲线表达式：

综合式（14）、（16），可以得到整条实测数据的拟合曲线表达式为

如图14所示为使用上述自然相交分段拟合方法，并经指数过渡曲线修正的拟合曲线.可以看出，在修正后的自然相交分段拟合结果中，各段曲线之间光滑衔接.

为了比较上述3种拟合方法的拟合结果，图15给出对同一组实测数据采用不同方式的拟合结果.可知，在曲线变化趋势及拟合精度等方面，指数过渡分段拟合优于传统多项式拟合.

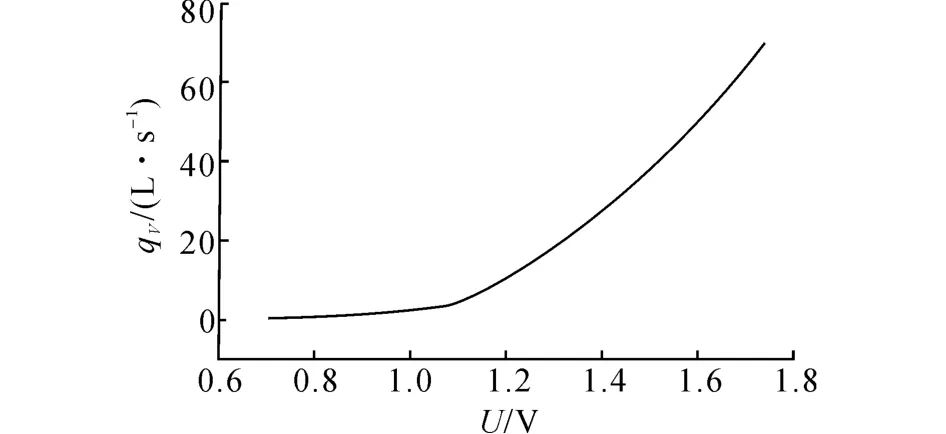
图14 指数过渡曲线修正分段拟合曲线Fig.14 Piecewise fitting curve with exponentialcurve-transition

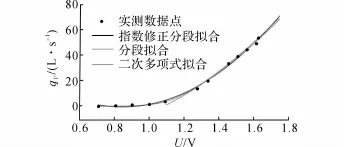
图15 3种方法的拟合曲线比较Fig.15 Fitting curves of three fitting methods

如表1所示为采用上述3种拟合方式所对应的拟合值及拟合误差.表1的结果显示，除了序号为8 和14的2个数据点外，分段拟合法的另外12个点分段拟合曲线的误差均小于传统的二次多项式拟合曲线的误差.计算3种拟合法的拟合方差，结果依次为：17.139 53、10.178178、9.862219.指数过渡分段拟合曲线的拟合精度最高，二次多项式曲线的拟合精度最低.

4 结 论

（1）多项式拟合在低流量范围内会出现单调递减的情况，造成拟合值对应的气体流量小于0.若增加多项式阶数，则会造成整条拟合曲线的延展性差，对原始数据范围外的预测值可信度降低.

（2）分段拟合往往难以达到“完美衔接”，在衔接点处常会出现较大的偏差，但在工程应用中，只要2段曲线在衔接点处的差值小于设定偏差，就可以满足精度要求.

（3）分段拟合具有较高的拟合精度，但会出现衔接点附近不光滑的情况，可以通过指数过渡曲线的修正来实现光滑处理.

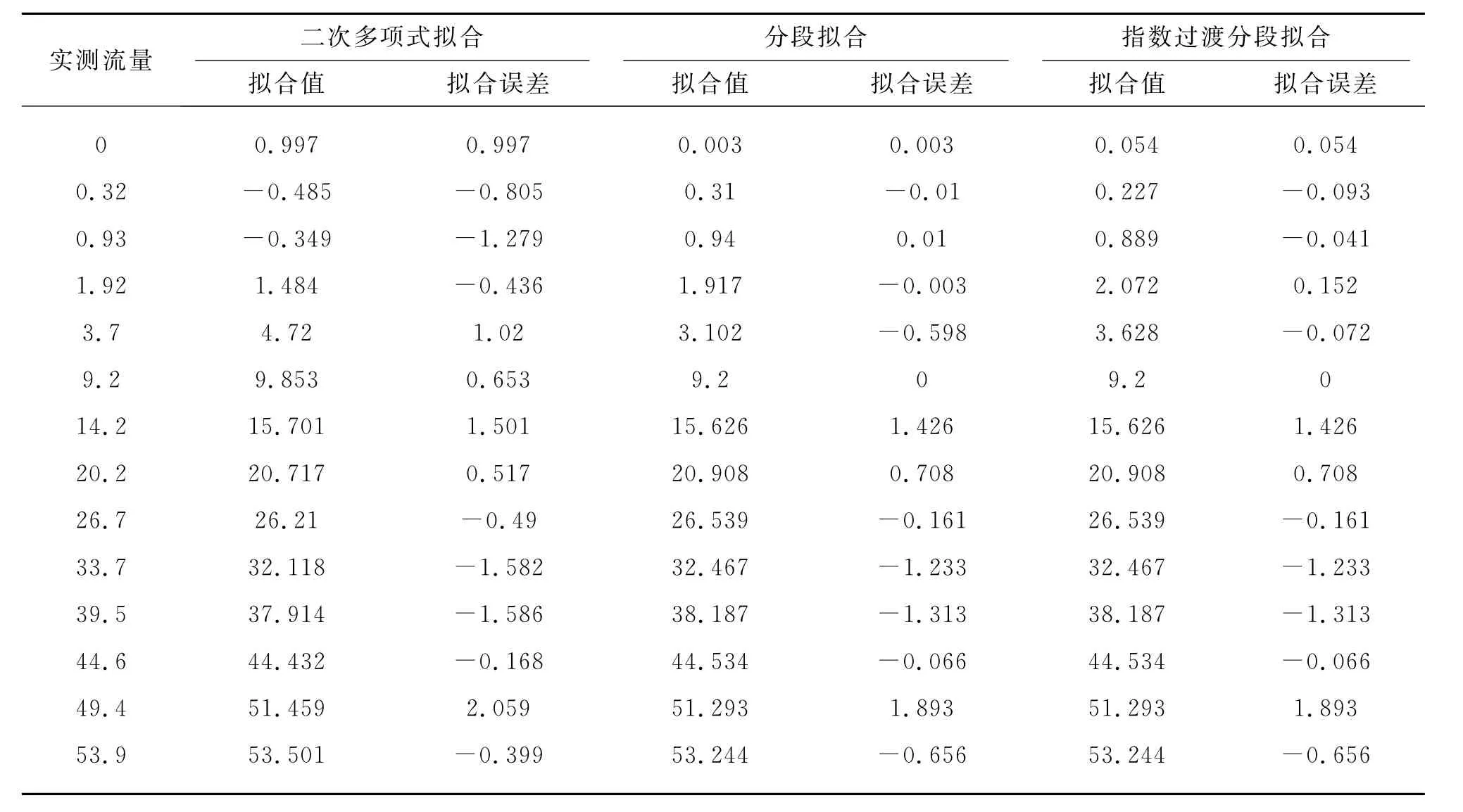
表1 3种拟合方法的结果对比Tab.1 Comparison of results of three fitting methodp L·s-1

（4）本文提出的分段拟合方法可以看作是一种介于无数据分析与处理的初步拟合方法与神经网络、支持向量机学习器方法这一类系统拟合方法之间的过渡方法，它结合了两者的优点.

（

）：

[1]梁国伟，蔡武昌.流量测量技术与仪表[M].北京：机械工业出版社，2002：350-364.

[2]腾勤，马标，徐科军.热膜式空气质量流量传感器块联模型结构辨识[J].仪器仪表学报，2008，29（3）：477-482.

TENG Qin，MA Biao，XU Ke-jun.Block-oriented model structure identification of hot film type mass air flow sensor[J].Chinese Journal of Scientific Instrument，2008，29（3）：477-482.

[3]闫宗魁.气体流量标准装置计算机测控系统的研究与设计[D].天津：天津大学，2005.

YAN Zong-kui.Research and design on computer control calibration system with gas flow standard device [D].Tianjin：Tianjin University，2005.

[4]蔡春丽，刘志远，王惠玲.基于恒温法的热膜式气体流量传感器的设计[J].传感器与微系统，2009，28（6）：104-109.

CAI Chun-li，LIU Zhi-yuan，WANG Hui-ling.Design of hot-film air flow sensor based on method of constant temperature[J].Transducer and Microsystem Technologies，2009，28（6）：104-109.

[5]赵伟国，宋执环，黄震威.基于热膜探头的新型气体流量传感器研究[J].仪器仪表学报，2009，30（5）：1073-1077.

ZHAO Wei-guo，SONG Zhi-huan，HUANG Zhen-wei.Study on new gas flow sensor based on hot-film probe [J].Chinese Journal of Scientific Instrument，2009，30（5）：1073-1077.

[6]VAPNIK V.The nature of statistical learning theory [M].New York：Springer，1995.

[7]KEWLEY R H，EMBRECHTS M J，BRENEMAN C.Data strip mining for the virtual design of pharmaceuticals with neural networks[J].IEEE Transaction on Neural Networks，2000，11（3）：668-679.

[8]CHEUNG W K，ZHANG X F，WONG H F.Serviceoriented distributed data mining[J].IEEE Internet Computing，2006，10（4）：44-54.

[9]PONNI J，SHUNMUGANATHAN K L.Multi-agent system for data classification from data mining using SVM[C]∥Green Computing，Communication and Conservation of Energy.Chennai：IEEE，2013：828-832.

[10]余柏林，王瑞春，龚汉东.环境温度对集成微沟道温差空气流量传感器的影响与补偿[J].传感技术学报，2011，24（5）：684-687.

YU Bo-lin，WANG Rui-chun，GONG Han-dong.The effects and compensation of ambient temperature on an air flow sensor integrated micro channel[J].Chinese Journal of Sensors and Actuators，2011，24（5）：684-687.

[11]李辉，张持健.一种高性能MEMS气体流量传感器设计[J].传感器与微系统，2014（33）：77-79.

LI Hui，ZHANG Chi-jian.Design of a high performance MEMS gas flow sensor[J].Transducer and Micr-osystem Technologies，2014（33）：77-79.

[12]黄硕.微型热式气体流量传感器的稳态传热研究[D].杭州：浙江大学，2009.

HUANG Shuo.Study on the steady heat transfer of the micro thermal airflow sensor[D].Hangzhou：Zhejiang University，2009.

[13]杨辉华，简捷.热式质量流量计特性曲线及其拟合方法的研究[J].化工自动化及仪表，1996，23（6）：37-41.

YANG Hui-hua，JIAN Jie.Study on the characteristics of thermal mass flow meter and its curve fitting [J].Control and Instruments in Chemical Industry，1996，23（6）：37-41.

[14]SUN J H，CUI D F，ZHANG L L.A micromachined gas flow sensor with polydimethylsiloxane flow channels[J].IEEE/ASME Journal of Microelectromechanical Systems，2013，22（3）：723-729.

Curve piecewise fitting method with exponential-curve-transition of hot-film gas flow sensors

PENG Dan，YANG Lei，YANG Jia-qiang

（College of Electrical Engineering，Zhejiang University，Hangzhou 310027，China）

A simple and new piecewise fitting method was proposed based on polynomial fitting and piecewise fitting methods in order to improve fitting accuracy of the output curve of a hot-film gas flow sensor which is applied to air duct of a high speed train to monitor the motion state of the high speed train.An exponential curve was used as the transition interval between the dividing parts.A dividing point was artificially chosen from the raw data，which means that the raw data was divided into two parts and two fitting curves were subsequently obtained.An intersection point was got with the two fitting curves.The transition area was formed between the two points of the raw data prior to and next to the intersection point.After the processing steps mentioned above，the transition area was corrected with an exponential curve so that a problem of unsmooth connection was solved.Fitting results of polynomial fitting，piecewise fitting based on dividing point and the proposed fitting were given and compared in order to verify the proposed curve fitting method.Results show that the proposed fitting method has the highest accuracy and its curve fitting errors are within1.5％for all intervals.

gas flow sensor；curve fitting；polynomial；subsection；natural-intersection；exponentialcurve-transition

TP212

A

1008-973X（2015）10-1990-09

2014-11-12.浙江大学学报（工学版）网址：www.journals.zju.edu.cn/eng

彭丹（1985—），男，硕士，从事飞轮储能系统控制、智能传感器的研究.ORCID：0000-0001-6502-1345.

E-mail：pengdan-85@163.com

杨家强，男，副教授.ORCID：0000-0002-3822-3301.E-mail：yjq1998@163.com