环形轨自动化制孔系统孔位修正方法

毕运波，涂国娇，方 伟，沈立恒，李汝鹏

（1.浙江大学机械工程学系，浙江杭州310027；2.浙江大学土木工程学系，浙江杭州310027）

环形轨自动化制孔系统孔位修正方法

毕运波1，涂国娇1，方 伟2，沈立恒2，李汝鹏2

（1.浙江大学机械工程学系，浙江杭州310027；2.浙江大学土木工程学系，浙江杭州310027）

为了满足大型飞机机身段壁板对接面区域的高质量制孔要求，提出基于六轴联动环形轨自动化制孔系统的孔位修正方法.该方法采用激光位移传感器以非接触测量的方式测量并求解得到基准孔的法矢，结合视觉测量系统获取的基准孔孔位误差，通过插值Coons曲面方法计算待加工孔的孔位误差向量，并补偿至理论坐标，实现孔位修正.利用筒状飞机机身壁板模型对该方法进行验证.结果表明，与双线性插补方法相比，该方法综合考虑了壁板外形表面曲率变化因素，孔位修正精度较高，保证了机身段壁板对接区域制孔的几何精度要求.

环形轨自动化制孔系统；激光位移传感器；法矢；Coons曲面；孔位修正

在飞机装配过程中，飞机结构件之间的连接通常以机械连接为主，而连接孔加工和装配质量对于提高连接精度、保证飞机使用寿命及安全性有重要影响.据统计可知，70％的飞机机体疲劳失效事故起因于结构连接部位，其中80％的疲劳裂纹往往发生于连接孔处[1].为了提高飞机装配质量和效率，可以采用自动化制孔设备改善连接孔的加工精度和质量.环形轨自动化制孔系统作为一种重要的自动化制孔设备，主要用于实现机身段壁板对接面区域制孔.由于壁板对接面区域待加工孔的理论孔位与实际孔位之间存在偏差，导致末端执行器难以实现精确定位.产品制造几何误差、温度变化引起的热变形误差及自重导致的变形误差等因素都可以导致孔位偏差.为了保证实际孔间距和排距的均匀分布，有必要对理论孔位置进行修正.在对孔位修正技术的研究中，Zhu等[2]通过基于制孔区域的基准孔误差向量构建双线性误差平面，实现了对制孔区域的孔位进行线性插值补偿.机身段壁板对接区域主要由二次曲面及三次曲面构成，且孔位误差与壁板的曲率有关，故双线性插值补偿方法存在一定的局限性.

为了准确表达机身段壁板对接面处的二次曲面和三次曲面，本文在构建孔位误差补偿模型过程中引入了曲面法矢信息.在法矢计算的相关研究中，薛汉杰等[3]采用三点接触式位移传感器实现法向调整，但由于接触式位移传感器精度较低，法向调整精度较难保证.秦现生等[4]利用机翼表面上待钻铆点附近三点的坐标表征钻铆区域的空间姿态.为了防止由于某一点误差较大而影响法矢的计算精度，目前较普遍的方法是根据待钻铆点附近四点的坐标表征该点的法矢.张来喜等[5]提出的四点拟合球面算法，以球面近似代表制孔点区域曲面，并用制孔点在球面上的法向量近似代表制孔点的曲面法矢，但对于与球面曲率相差较大的曲面，法矢计算较复杂且精度较低.邹冀华等[6]通过4个安装高度一致的激光位移传感器调整法向，虽然实现了高精度的法向调整，但对激光位移传感器的装配工艺要求提出了更高的要求.

针对以上问题，本文提出一种面向六轴联动环形轨自动化制孔系统的孔位修正方法.该方法利用激光位移传感器测距获得基准孔周围区域的四点坐标，并计算得到基准孔法矢；结合视觉测量系统测得的基准孔位偏差，构建孔位误差补偿模型，并利用该补偿模型修正孔位理论坐标，从而提高制孔精度，保证制孔质量.

1 环形轨自动化制孔设备

环形轨自动化制孔系统可以在程序驱动下实现六轴联动的数字控制、加工孔深控制、压脚压力自动气动调节、加工表面法向测量、孔位修正等功能.凭借导轨上的真空吸盘，可以吸附于飞机壁板进行制孔，且制孔效率高、质量好，使用较方便和灵活[7].如图1所示，该系统主要由末端执行器、环形轨道、保持架、下部托架等部件组成.

环形轨末端执行器即环形轨制孔设备，可以实现在弧形段区间内5自由度的自动化制孔.如图2所示，该设备由X向托板、A轴转台、Y向托板、B轴转台、Z1轴托板、Z2轴托板及压脚、激光位移传感器（法向检测单元）、视觉测量系统等组成[8].

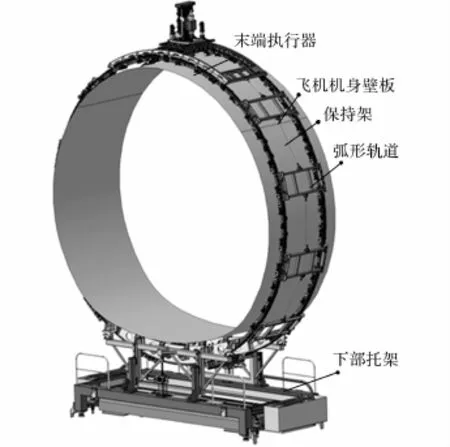
图1 环形轨自动化制孔系统Fig.1 Flexible track automatic drilling system

图2 环形轨末端执行器Fig.2 End-effector of flexible track automatic drilling system

2 孔位修正原理

在环形轨自动化制孔系统中，首先视觉测量系统可以测量得到在视觉系统坐标系下的基准孔坐标QT.考虑到视觉坐标系通常与飞机坐标系不重合，将QT转化为在飞机坐标系下的基准孔实际坐标Qt，并将Qt与离线编程系统输出的基准孔理论坐标Q＇t比较，从而得到4个基准孔误差向量ΔPi（i=1，2，3，4）.末端执行器上的4个激光位移传感器可以测得每个基准孔周围的4点坐标（xi，yi，zi），由此可以求解出各基准孔法矢ni.结合ΔPi和ni（i=1，2，3，4）拟合Coons曲面构建误差曲面函数ΔQ（u，ω），利用待加工孔坐标计算出孔位误差ΔQ*，并补偿到该孔的理论坐标Q上进行孔位修正，得到新的理论坐标Q*，计算过程如图3所示.

3 孔位修正方法

3.1 法矢计算

法向检测单元是制孔孔位法向修正的重要部件，由位于压脚前端的4个激光位移传感器A1、A2、A3和A4组成，激光位移传感器能够以非接触测量的方式精确测得与被测物体之间的距离.标定后的法向检测单元可以确定激光位移传感器的位置坐标以及激光发射的方向向量[9].可以确定飞机壁板上激光投影点Q1、Q2、Q3和Q4的坐标（xi，yi，zi）（i=1，2，3，4）.投影点连线的中点分别为M1、M2、M3和M4，如图4所示为待加工孔法矢的计算示意图.

由几何学基础可知，M1、M2、M3和M4的坐标为两端点坐标之和的1/2，结合三角形中位线定理可知，M1M2∥Q1Q3∥M3M4和M1M4∥Q2Q4∥M2M3.根据平行四边形判定原理，可以推得M1、M2、M3和M4位于同一平面且组成平行四边形.平面M1M2M3M4的单位法矢n可以由平行四边形任意相邻边的向量积计算得到：

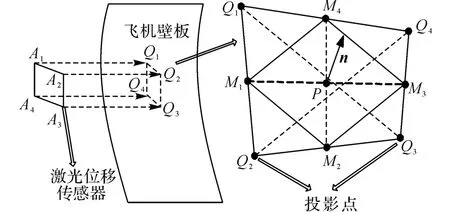
图4 法矢计算示意图Fig.4 Calculation of normal vectors

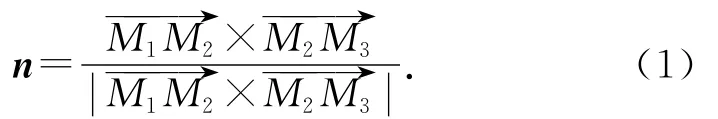
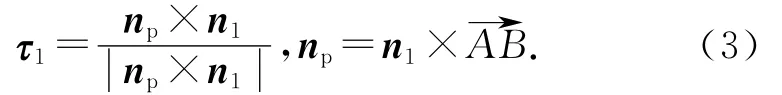
同理，可以分别得到B、C、D三点的切矢分别为τ2、τ3、τ4.

切矢的模长影响曲线段的丰满程度，如图6所示.图中，t为图中实线首末端点切矢的模长，2t、10t、20t分别为其他3条曲线首末端点的切矢模长.由图6可得，当端点坐标相同时，切矢模长越大，曲线越丰满.为了得到理想的曲线段，一般切矢模长不应超过弦长的3倍[11]，在实际应用中以拟合曲线最接近实际曲线的切矢模长为理想的切矢模长.

3.2 基准孔位误差计算

由视觉测量系统可得视觉系统坐标系下飞机壁板上4个基准孔的坐标.通过建立视觉系统坐标系和飞机坐标系之间的转换关系，得到在飞机坐标系下基准孔的实际坐标Qt[7].将Qt与离线编程中基准孔的理论坐标Q＇t之间的偏差ΔP作为孔位误差[10]，计算方法如下所示：

由式（2）可得飞机壁板上基准孔的孔位误差，可以表示为：ΔPi=（Δxi，Δyi，Δzi）（i=1，2，3，4）.

3.3 孔位误差曲面拟合和修正

3.3.1 切矢计算 采用构造双线性Coons曲面的方法拟合误差曲面函数.首先以Ferguson曲线拟合制孔区域垂直于航向的2条理想边界曲线，然后以直线拟合航向的2条理想边界曲线.

拟合Ferguson曲线需要知道各端点的切矢，如图5所示为切矢计算示意图.分别以A、B、C、D表示各基准孔，P1、P2、P3和P4表示各基准孔坐标（xi，yi，zi）（i=1，2，3，4）.由3.1节所述的法矢计算方法可得各基准孔的法矢分别为：n1、n2、n3和n4.设向量AB→和n1构造的平面为α，np为平面α的法向量，则A点的单位切矢为

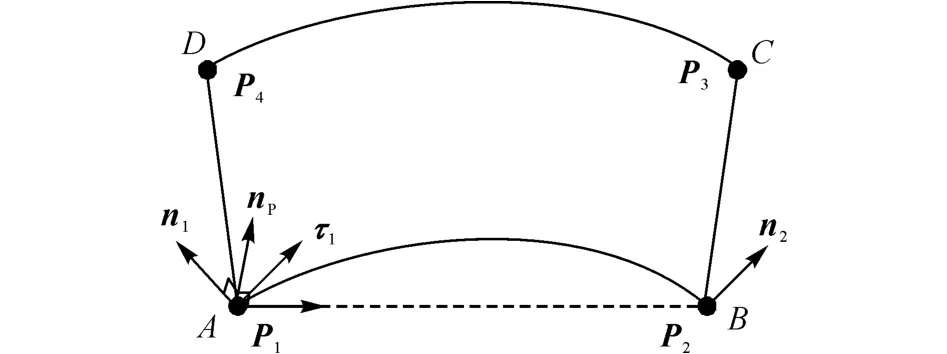
图5 切矢计算示意图Fig.5 Calculation of tangential vectors

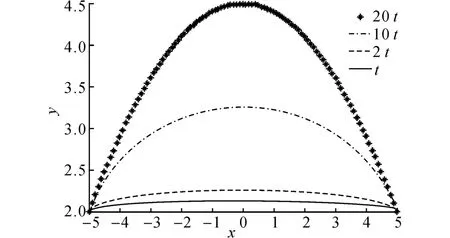
图6 切矢模长对曲线段丰满程度的影响Fig.6 Effects of tangent vectors length have on curves

3.3.2 Ferguson曲线拟合 Ferguson首先在飞机设计中应用了参数三次曲线[12-13]，曲线段的表达式为

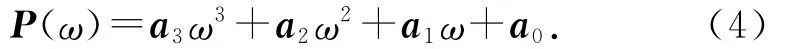
切矢为

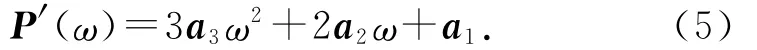
式中：ω∈[0，1.0]；a0、a1、a2、a3为待定矢量，给定曲线的首末端点P1、P2及切矢τ1、τ2，可以拟合曲线如下所示：

式中：

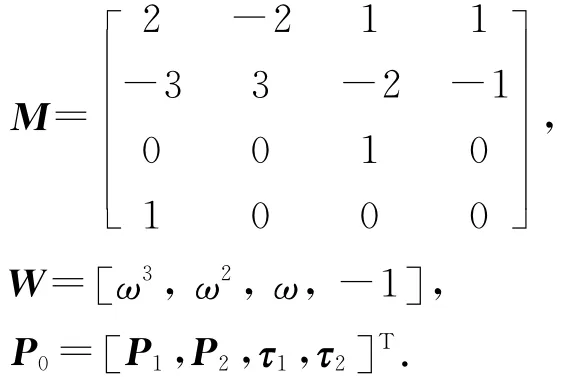
同理，拟合P3、P4之间的曲线有

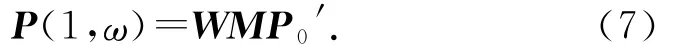
式中：

拟合后AB曲线方程为

CD曲线方程为

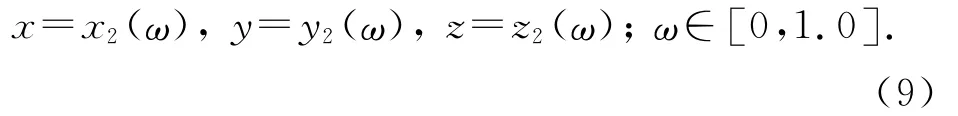
3.3.3 曲线严格上凸条件 根据凸曲线定理可知，曲线严格上凸的充分条件为曲线的Hessian矩阵严格负定[14].根据3.3.2节可得，Ferguson曲线方程f=f（x，y，z），Hessian矩阵为

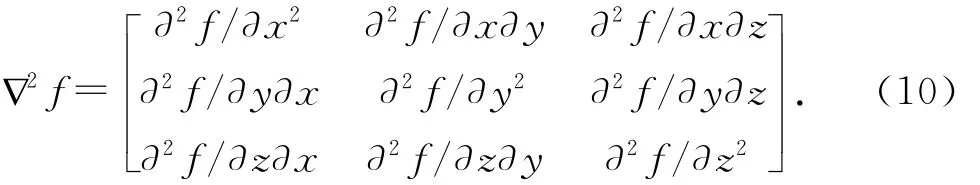
设N=∇2f，若对于任何向量U=[u1，u2，u3]T都有UTNU＜0，则称该Hessian矩阵负定，该条件可以用于验证并调整曲线切矢.

3.3.4 Coons曲面构造 由于环形轨自动化制孔系统的加工对象多为图7所示的飞机机身段壁板对接面区域，该类壁板沿飞机航向机身对接段区域的曲率变化较小，故P1P4、P2P3可以近似拟合成直线，表达式如下所示：

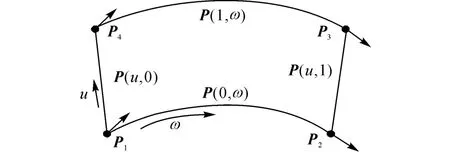
图7 曲线拟合示意图Fig.7 Interpolating curves of fuselage panel

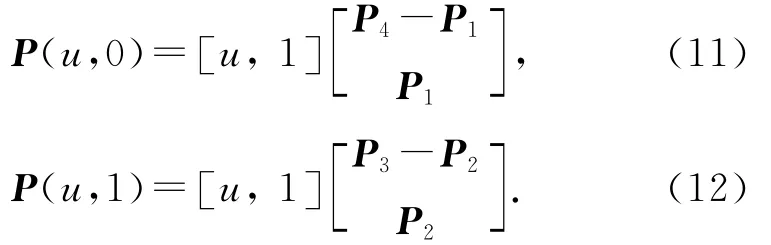
插值双线性Coons曲面[15]为

式中：

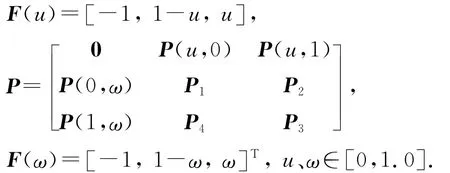
3.3.5 孔位修正 如图8所示，ΔP1、ΔP2、ΔP3、ΔP4为各基准孔的实际位置与理论位置的偏差向量.

根据3.3.4节所述的方法，可以拟合得到如下所示的制孔区域误差曲面函数：

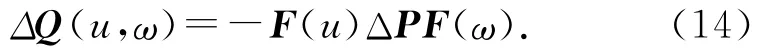
式中：

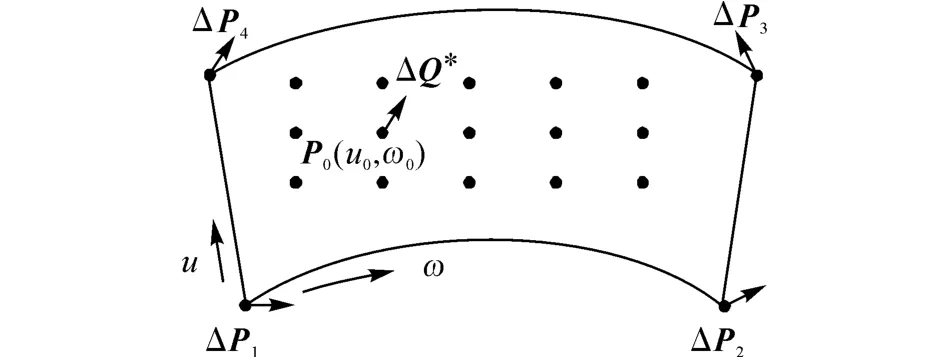
图8 孔位修正图Fig.8 Hole position correction

其中，

将制孔点坐标投影到图8所示的u、ω方向，可得该制孔点在u、ω方向的坐标u*、ω*，并将u*、ω*代入式（15），可得待加工区域任一点P0的误差向量：

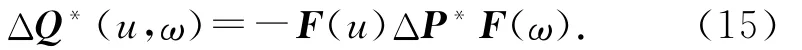
式中：

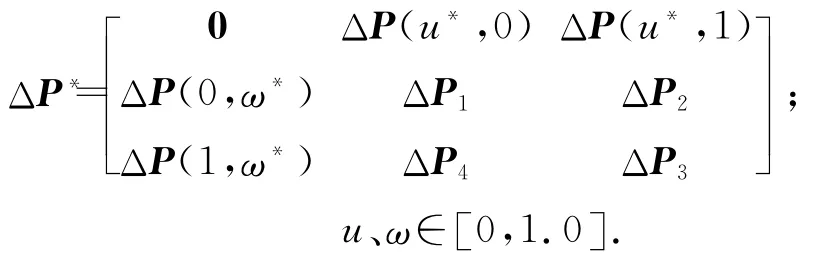
将ΔQ*补偿至待加工孔的理论坐标上即可实现孔位修正.

4 算例及试验

4.1 法矢求取算例

为了验证上述法矢计算方法的正确性与合理性，以下式所示的椭圆曲面为例进行说明：

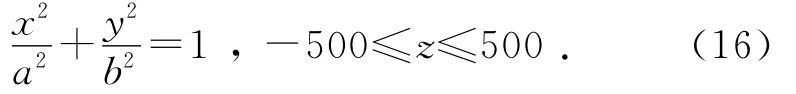
式中：a=3000，b=2000.M（420.791，1980.228，-53.445）为曲面上待加工孔位坐标，且M点处的曲面外法矢的理论值nthe=[0.094，0.996，0].如图9所示，记各位移传感器的安装平面为β，传感器探头位置A1、A2、A3、A4构成中心为A0的87 mm×92 mm的矩形，A0点和待加工点M均处于末端执行器的轴线上，实际检测过程中点M位置由控制系统读出.传感器以直线A0M的方向对曲面进行检测.其中A0M=91.367，可得A0坐标为（441.081，2069.314，-53.445），且4个位移传感器的检测值为A1M1=95.328，A2M2=80.689，A3M3=88.259，A4M4=102.085；求得在M点处的曲面外法矢为ncal=[-0.094，-0.996，0]，nthe与测量所得的外法矢ncal夹角的余弦值如下式所示：nthencal/（|nthe‖ncal|）≈1.该式表明，nthe与ncal的夹角近似为0，即两者近似平行，证明该法矢求取算法具有较高的精度.

图9 法矢求取示意图Fig.9 Calculation of normal vector

4.2 孔位修正算例

为了验证上述孔位修正算法的正确性与合理性，以下式所示的圆筒形飞机壁板为例进行验证.

具体步骤如下.

1）如图10所示，取壁板上夹角∠AOB=60°的区域为研究对象.其中A、B、C和D为该制孔区域的基准孔，孔位坐标及法矢如表1所示.AD和BC均为直线且相互平行，图中点为1～16均匀分布于制孔区域的孔位，即孔间距和排距分布均匀.

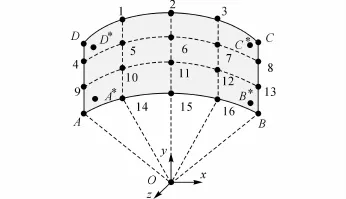
图10 孔位示意图Fig.10 Positions of all holes

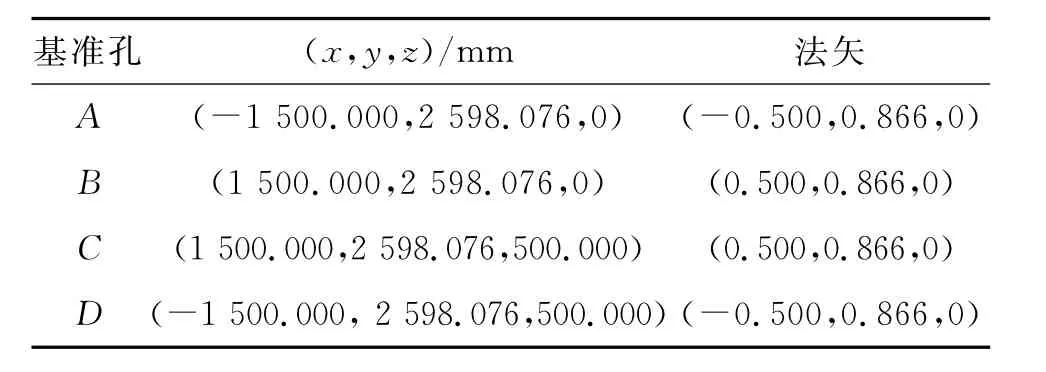
表1 基准孔位的理论坐标及法矢Tab.1 Nominalcoordinatesandnormalvectorsofreference holes

2）假设由于安装误差及制孔误差等因素的影响导致基准孔A、B、C、D偏移至如图10所示A*、B*、C*和D*的位置.基准孔的偏差如表2所示，为了保证待加工孔的间距和排距分布均匀，1～16孔偏移后的理想坐标值如表3所示.

表2 4个基准孔偏差Tab.2 Erroroffourreferenceholes

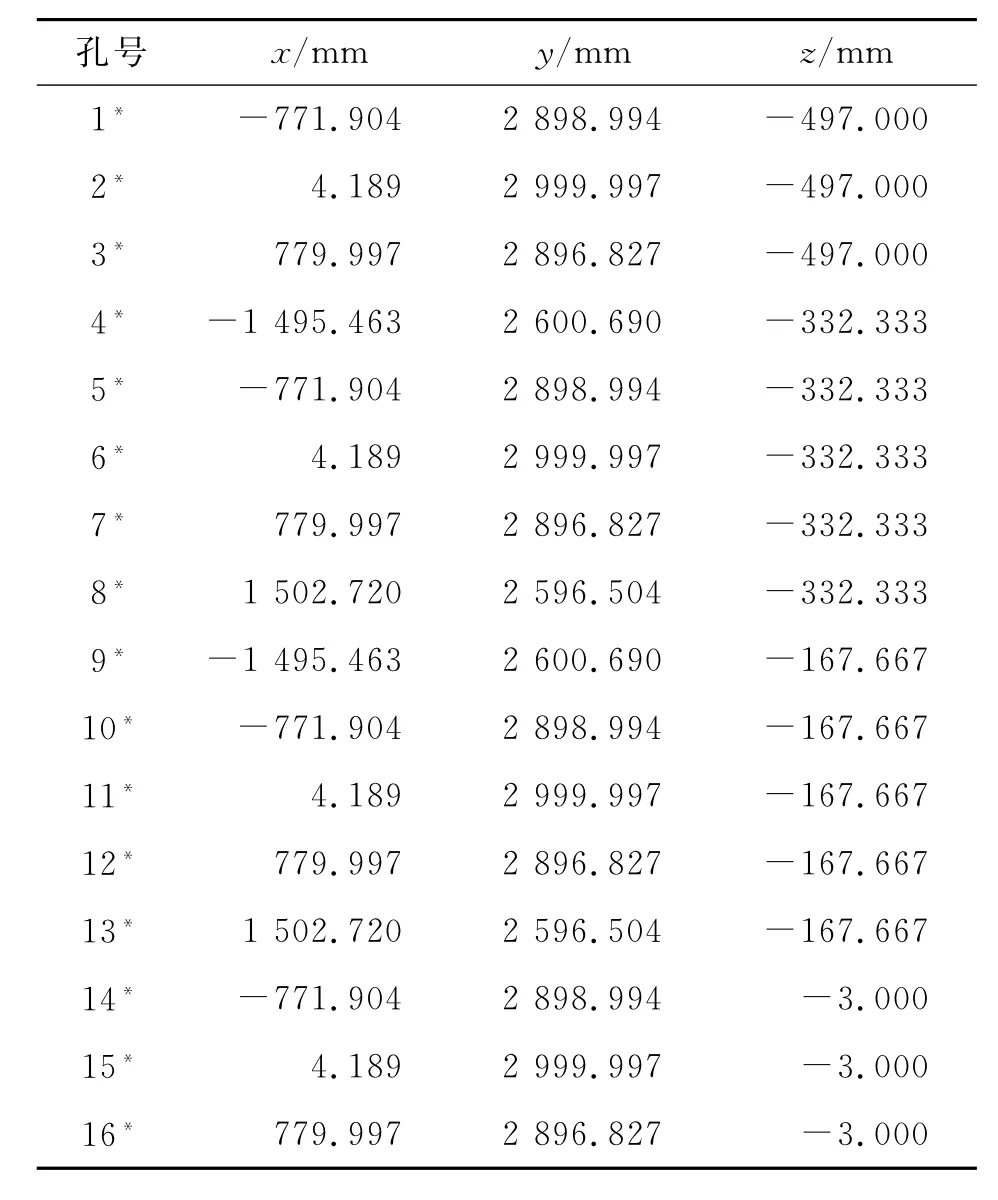
表3 偏移后各孔坐标Tab.3 Coordinatesof16holesaftertransformation

表4 孔位修正法插补后各孔坐标Tab.4 Coordinatesof16holesaftererrorinterpolating withmethodofpositioncorrection

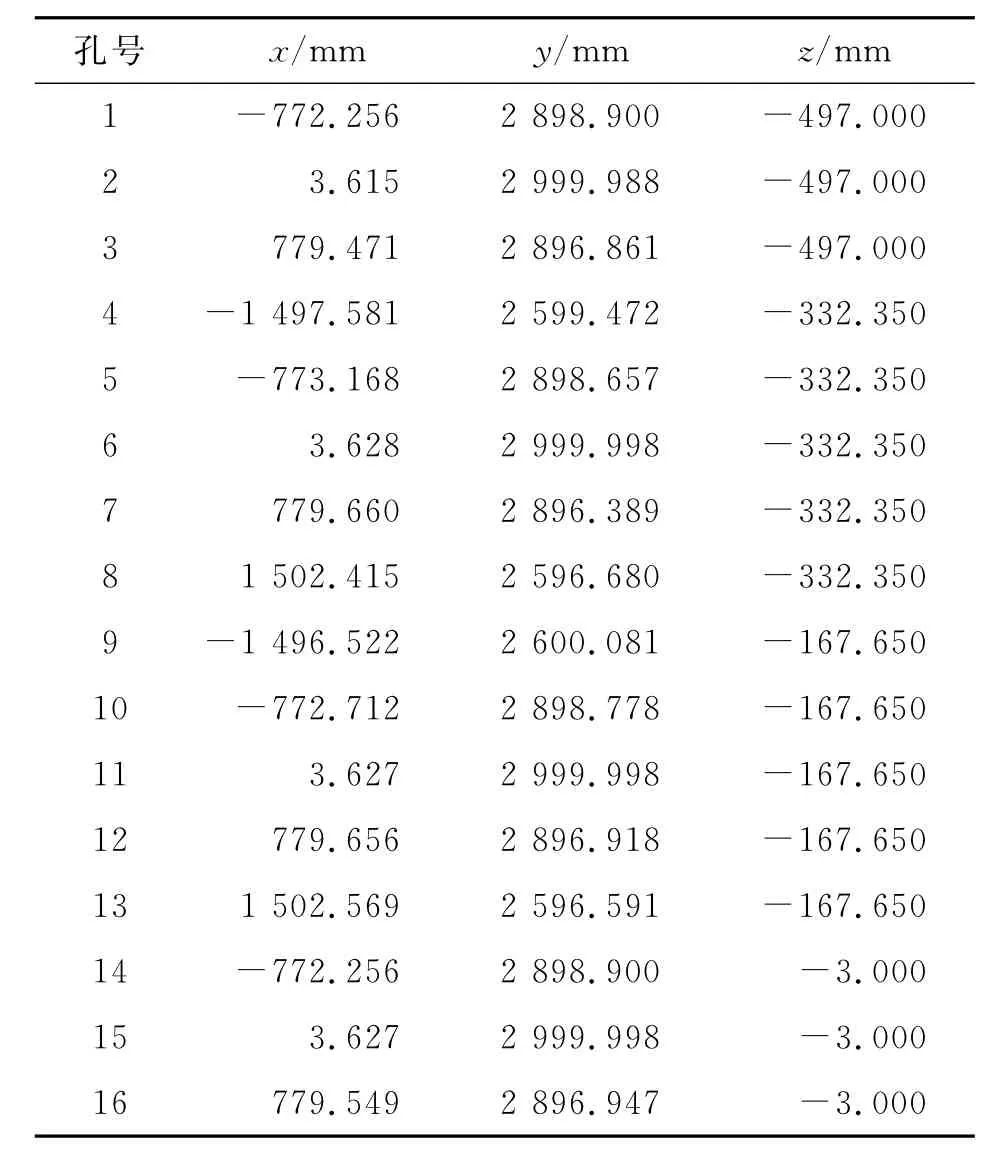
表5 双线性插补法修正后的各孔坐标Tab.5 Coordinatesof16holesaftererrorinterpolating withdoublelinearpositioncorrectionmethod

3）分别利用双线性插补和本文所述的孔位修正方法对待加工区域内的16个孔位进行孔位修正，并将修正后的坐标投影到壁板上.如表4和5所示分别为采用上述2种方法进行孔位修正后的各孔在壁板上的投影坐标.将投影点的坐标与表3中1～16孔的坐标比较得到的误差曲线分布如图11所示.图中，ΔE1为未修正时各孔的位置偏差，ΔE2为利用本文所述孔位修正方法插补后各孔的位置偏差，ΔE3为利用双线性插补方法进行孔位修正后各孔的位置偏差.

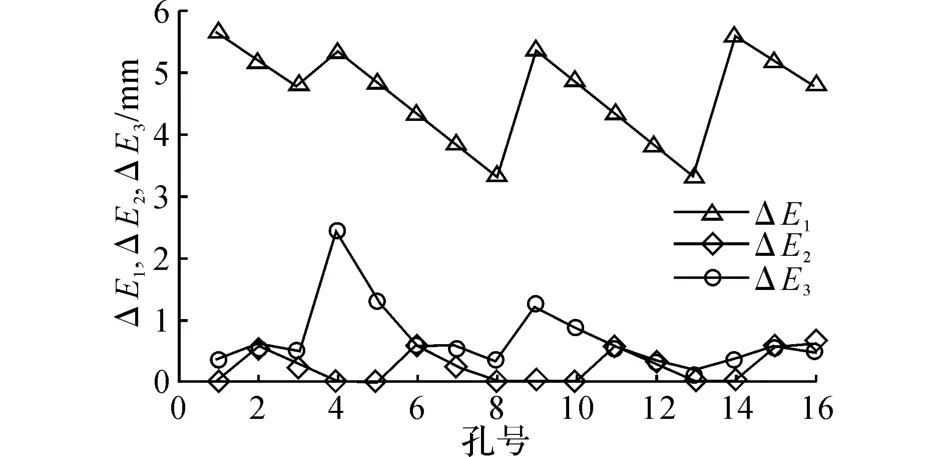
图11 各孔定位精度比较图Fig.11 Comparison of position errors of16 holes

在不进行补偿的情况下，与各孔的理论值相比，最大孔位偏差可达5.586 mm，而最小孔位偏差有3.302 mm；当采用双线性插补方法进行补偿后，最大孔位偏差减小至2.442 mm，而最小孔位偏差为0.175 mm；当采用本文方法进行误差补偿后，最大孔位偏差进一步减小，仅为0.628 mm，而最小孔位偏差只有0.005 mm，孔位精度得到明显提高.比较以上结果可知，本文所述的孔位修正方法可以明显地改善孔位间的相对位置精度，且孔位修正效果优于线性插补，满足机身段对接区域壁板制孔的几何精度要求.

5 结 论

（1）本文提出新的曲面法矢计算方法，能够快速、有效地获取壁板加工表面法矢信息.

（2）基于壁板加工表面法矢和孔位视觉测量数据，构建新的孔位误差曲面补偿模型，能够有效地修正孔位理论坐标，保证制孔精度.

（3）算例结果表明，本文提出的孔位修正方法综合考虑了壁板外形表面的曲率变化，孔位修正的效果优于线性插补方法.

（

）：

[1]许国康.自动钻铆技术及其在数字化装配中的应用[J].航空制造技术，2005（6）：45-49.

XU Guo-kang.Automatic riveting technology and the apply in digital assembly[J].Aeronautical Manufacturing Technology，2005（6）：45-49.

[2]ZHU W，QU W.An off-line programming system for robotic drilling in aerospace manufacturing[J].International Journal of Advanced Manufacturing Technology，2013，68（9-12）：2535-2545.

[3]薛汉杰，张敬佩.蒙皮类部件钻孔法向的测量和调整[J].航空制造技术，2010（23）：60-62.

XUE Han-jie，ZHANG Jing-pei.Normal measurement and adjustment for skin drilling[J].Aeronautical Manufacturing Technology，2010（23）：60-62.

[4]秦现生，汪文旦，楼阿莉，等.大型壁板数控制孔的三点快速调平算法[J].航空学报，2007，28（6）：1455-1460.

QIN Xian-sheng，WANG Wen-dan，LOU A-li，et al.Three-point bracket regulation algorithm for drilling and riveting of aerofoil[J].Acta Aeronautica et Astronautica Sinica，2007，28（6）：1455-1460.

[5]张来喜，王兴松.曲面柔性制孔机器人末端执行器及其法向姿态调整的一种新算法[J].东南大学学报：英文版，2012，28（1）：29-34.

ZHANG Lai-xi，WANG Xing-song.A novel algorithm of normal attitude regulation for the designed end-effector of a flexible drilling robot[J].Journal of Southeast University：English Edition，2012，28（1）：29-34.

[6]邹冀华，周万勇，韩先国.飞机装配中基于3-RPS的并联机构法向调整算法[J].中国机械工程，2011，22（5）：557-560.

ZOU Ji-hua，ZHOU Wan-yong，HAN Xian-guo.Normal adjusting algorithm of a 3-RPS parallel mechanism in airplane assembly[J].China Mechanical Engineering，2011，22（5）：557-560.

[7]BI Yun-bo，JIANG Yi-hang，LI Yong-chao，et al.A new flexible track automatic drilling system[J].Mechanics and Materials，2013，433-435：2178-2183.

[8]江一行.环形轨自动化制孔系统开发及其运动学方程解析[D].杭州：浙江大学，2014.

JIANG Yi-hang.Development andkinematics equation analysis of flexible track automatic drilling system[D].Hangzhou：Zhejiang University，2014.

[9]毕运波，李永超，顾金伟，等.机器人自动化制孔系统[J].浙江大学学报：工学版，2014，48（8）：1427-1433.BI Yun-bo，LI Yong-chao，GU Jin-wei，et al.Robotic automatic drilling system[J].Journal of Zhejiang University：Engineering Science，2014，48（8）：1427-1433.

[10]TIAN Wei，ZHOU Wei-xue，ZHOU Wei，et al.Autonormalization algorithm for robotic precision drilling system in aircraft component assembly[J].Chinese Journal of Aeronautics，2013，26（2）：495-500.

[11]FAUX I D，PRAT M J.Computational geometry for design and manufacture[M].Chichester：Ellis Horwood Ltd，1979.

[12]FERGUSON J C.Multivariable curve interpolation，report No.D2-22504[R].Seattle：The Boeing Company，1963.

[13]FERGUSON J C.Multivariable curve interpolation [J].Journal of the ACM，1964，11（2）：221-228.

[14]BOYD S，VANDENBERGHE L.Convex optimization [M].England：Cambridge University Press，1906.

[15]朱心雄.自由曲线曲面造型技术[M].北京：科学出版社，2000.

Correcting method of hole position for flexible track automatic drilling system

BI Yun-bo1，TU Guo-jiao1，FANG Wei2，SHEN Li-heng2，LI Ru-peng2

（1.Department of Mechanical Engineering，Zhejiang University，Hangzhou 310027，China；2.Department of Civil Engineering，Zhejiang University，Hangzhou 310027，China）

A method of hole position correction for a flexible track automatic drilling system with six axes was proposed in order to meet the high drilling accuracy requirement of aerospace fuselage join assembly.The method was presented by measuring and computing the normal vector of the reference holes through four non-contact laser displacement sensors.The error of reference holes can be obtained based on the vision measurement system.A position correction method using error data of reference holes was developed by interpolating the Coons surface.Then the position correction can be realized by adding error to the nominal coordinates of the holes.The method was tested on a cylinder model.Results indicate that the method accounting for the changing curvature of the panel shape has higher accuracy of hole position correction and can effectively meet the geometric accuracy requirement of aircraft panels compared with the double linear interpolating method.

flexible track automatic drilling system；laser displacement sensor；normal vector；Coons surface；hole position correction

TH12

A

1008-973X（2015）10-1863-07

2014-09-05.浙江大学学报（工学版）网址：www.journals.zju.edu.cn/eng

国家自然科学基金资助项目（51275463）.

毕运波（1979—），男，副教授，从事飞机数字化装配技术的研究.ORCID：0000-0002-6270-3030.E-mail：zjubyb@zju.edu.cn