多色点集直线划分的复杂性及其近似算法
2015-01-06陈崇琛RudolfFleischer
陈崇琛,Rudolf Fleischer
(复旦大学计算机科学技术学院,上海201203)
多色点集直线划分的复杂性及其近似算法
陈崇琛,Rudolf Fleischer
(复旦大学计算机科学技术学院,上海201203)
多色点集划分研究如何将含有不同颜色点的平面划分为各个区域,每个区域中只包含一种颜色的点。这是计算几何中的一种组合优化问题。但是现有的多边形划分方式性能较差。为此,提出用直线来划分平面。针对平面上多色点集的直线划分,将其离散化,证明其可以被非确定性图灵机在多项式时间内判定。并将Max2SAT问题在多项式时间内归约到组合优化问题,证明多色点集直线划分为NP难,从而证明其是NP完全的。利用最优化版本的特有性质,运用贪心方法构造出多项式时间的近似算法,并L归约到Setcover问题,以此证明算法的近似比为O(lgn)。
计算几何;计算复杂性;近似算法;划分算法;组合优化;NP完全
1 概述
在计算几何中有一类重要问题就是处理划分多色的点集[1-2]。多色点集划分问题是将平面上不同颜色的点集划分成单色的区域,已经被广泛研究[3]。研究这些问题对于数字信号中的噪声处理非常有用[4]。但是目前研究的问题大多是将不同颜色的点划分进不同的凸多边形,使得每个多边形内部都只有一种颜色[5],或者更加简单,不考虑多边形的凹凸[6]。
多色点集多边形划分目前较好的结果是达到最多O(n/c)个多边形可以划分平面,其中c为常数,n为输入规模[7]。但是对于n个点的点集,都能用n个多边形划分。其算法和朴素算法之间性能差异小,结果的复杂程度都和输入规模线性相关,且无法衡量解和最优解之间的差距。且结果复杂程度尚未考虑到多边形本身边数的复杂。于是提出新的划分方法,采用直线划分。多色点集直线划分是用尽量少的直线(而非多边形),将颜色混杂的平面划分为单色的区域。
本文通过将其离散化,证明其可以被非确定性图灵机在多项式时间内判定,并从Max2SAT问题进行归约,证明其NP完全的复杂性,并且提出一个高效的近似算法来解决这个问题。
2 相关定义
2.1 多色点集直线划分
输入平面上给定n个点,每个点都有一种颜色,总共有k种颜色。
输出是否存在l条直线将平面分割成若干区域,使得每个区域中的点都具有相同颜色。
2.2 Max2SAT问题
输入布尔子句集合C=(C1,C2,…,Cm),每个子句包含2个文字,集合中总共含有变量x1,x2,…,xn。
输出给定k,是否存在一个赋值,使得C中至少有k个子句值为真。
2.3 L归约
一个从问题A到问题B的L归约是一对函数R和S,函数都能在对数空间内计算,如果x是A的一个有最优花费OPT(x)的实例,则R(x)是B的一个实例,其最优花费满足:

其中,α是一个正的常数。
如果s是R(x)的任意可行解,则S(s)是x的一个可行解,使得:

其中,β是另一个与归约相关的正常数;c表示2个实例的花费。
如果一个归约能够满足L归约的性质,那么这个归约能够保证问题的近似比[8]。
2.4 SETCOVER问题
输入元素集合S={a1,a2,…,an},以及一个集合的集合A={A1,A2,…,Am},Ai是S的子集。
输出,B是A的一个子集,使得S,且最小化。
3 复杂性
对于给定的问题实例,输出为“是”当且仅当对于这个实例存在一个直线数目小于等于l的合法划分,该划分的每一条直线都非常接近输入中的某2个点。接近的含义是,对于输入中的任意点A,可以构造点(xA,yA±ε),其中,xA,yA是点A的横纵坐标。如果输入的点的横纵坐标都能用N个比特表示,那么ε是一个正常量,且ε<1/(22N+1)。每一条划分直线都经过某2个新构造的点。
证明:如果给定实例的答案是“是”,但是作为证据的划分中存在某些线,至多接近输入中的一个点。那么将这条线进行旋转,直到这条线接近某个输入的点,然后以该点为中心进行旋转,直到接近输入的另一个点,如图1所示。

图1 旋转线的移动
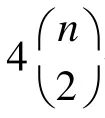
图2中的2个点,总共确定4条线,它们所划分点的情况是不一样的。
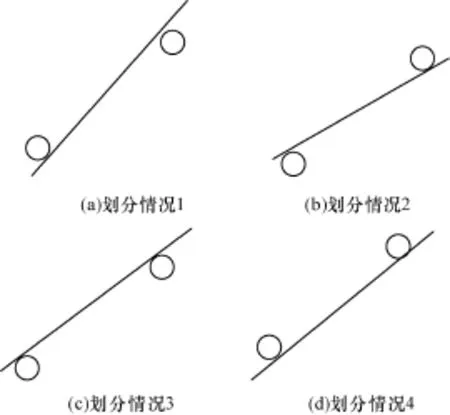
图2 4条可行线的确定
如果给定实例中的l不小于n,那么问题的答案永远是“是”。在这个实例中,线数至多足以使每个区域只有一个点,自然是满足单色要求的。可以用朴素的算法进行划分。所以下面只考虑l小于n的情况。
引理1多色点集直线划分问题在NP类中。
接下来证明问题是NP完全的。通过将Max2SAT问题在多项式时间内归约到多色点集直线划分问题来证明。Max2SAT是一个著名的NP完全问题[9]。
定理多色点集直线划分问题是NP完全的。
证明:给定一个Max2SAT的实例,将在多项式时间内构造一个多色点集直线划分问题的实例。并且证明构造的多色点集直线划分问题的实例能够被至多l条线划分当且仅当给定的Max2SAT的实例存在一个赋值使得C中至少有lb个子句为“真”。对于Max2SAT中的变量和子句构造不同的零件,然后将这些零件在平面上拼起来,得到目标中的多色点集直线划分的实例。
对于Max2SAT中的每个变量构造一个零件。一个变量零件包含a2+(a-1)2个小的菱形,2个对角线方向相邻的菱形的颜色是不同的,且其相邻的顶点非常接近,即2个顶点的距离不超过ε,ε的定义与观察1中一样。其中,a2个为其中一种颜色, (a-1)2个为另一种颜色,如图3所示。如果想要用2(a-1)条直线来分割这个零件,只有2种可能的方式,如图4所示。

图3 变量零件
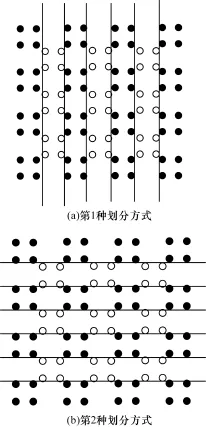
图4 2种划分变量零件的方式
考虑2个相邻菱形的相邻定点对,如果想要划分整个零件,那么必须有一条直线通过这个相邻异色顶点对。对于任意的线,至多通过2(a-1)个相邻异色顶点对。总共有(2(a-1))2个相邻异色顶点对。但是只有2(a-1)条直线,每条直线平均划分(2(a-1))2/(2(a-1))=2(a-1)个相邻异色顶点对,因此每条直线都划分2(a-1)个相邻异色顶点对。因此,划分的直线一定是只有横竖2种。假设得到的解中,既有横的直线,也有竖的直线,那么必定有部分划分的相邻异色顶点对是重复的。2(a-1)条直线划分的相邻异色顶点对数小于(2(a-1))2,得到矛盾。于是得到上文的2种最优划分方式。
将其中一种划分方式表示Max2SAT中的变量取值为“真”,称之为“真划分”;另一种划分方式表示Max2SAT中的变量取值为“假”,称之为“假划分”。
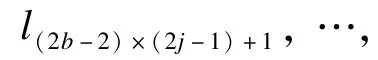

图5 构造的细节
对于Max2SAT问题,假设不会存在一个子句同时包含x和¬x,这些子句永远是为“真”。可以在做归约之前,在多项式时间内去掉。取b=2。
下面情况之一发生,定义平面上零件发生相互影响:
(1)存在某条直线不属于某个零件的“真划分线”,或者“假划分线”,但是却划分了属于不同零件的2个以上相邻异色点对。
(2)存在某条直线属于某个子句零件的“真划分线”或者“假划分线”,但是却划分了其他子句零件中的相邻异色点对,或者该子句中不包含的变量零件的相邻异色点对。
(3)存在某条直线属于某个变量零件的“真划分线”或者“假划分线”,但是却划分了其他变量零件或者不包含该变量的子句的零件。
引理2如果每个零件的划分不会相互影响,那么原来的有n个变量和m个子句的Max2SAT问题实例能够满足至少lb个子句,当且仅当构造的多色点集直线划分问题实例能够被至多l=2n(a-1)+ 2(m-lb)(b-1)条直线划分。
证明:现在假定每个零件之间不会相互影响。
如果原来的有n个变量和m个子句的Max2SAT问题能够满足至少lb个子句,那么每个变量零件能够被2(a-1)条线满足,在划分变量零件时顺带划分的已经满足的子句零件就不需要重复划分了,这部分的子句数目是lb,那么仍需要划分的子句数目至多为m-lb,每个子句至多需要2(b-1)条直线来划分,所以构造的多色点集直线划分问题实例至多需要被l=2n(a-1)+2(m-lb)(b-1)条直线划分。
如果构造的多色点集直线划分实例能够被至多l条直线划分。因为零件之间不相互影响,所以划分变量零件需要2n(a-1)条直线。故剩余l-2n(a-1)条直线来划分子句零件。因此,至多(l-2n(a-1))/(2(b-1))个子句没有被满足,否则就有零件不能被划分,故满足的子句至少为lb=m-(l-2n(a-1))/(2(b-1))。
接下来说明如何设置a,b以及零件的位置,使得零件之间不会相互影响。
因为每条线由2个点决定,迭代添加变量零件(及相关的子句零件),每次添加时判断是否存在相互影响,然后通过移动,去除相互影响。算法1是构造算法:
在数学教学过程中,教师应拓展游戏内容,将生活中的数学元素融入到游戏教学中,拓展学生思维,丰富游戏内容,使学生在游戏中学习到数学知识,并应用于实际生活中。例如,在游戏教学中,教师可以组织学生玩儿老鹰捉小鸡游戏,每当老鹰捉住一只小鸡时,教师可以向学生提问:鸡妈妈现在还剩多少小鸡。通过游戏的方式让学生收获知识,获得快乐,生活与学习相结合,为学生创建轻松的学习环境,提升数学教学有效性[3]。
算法1计算零件位置的算法


可以看到函数addGadget最多被调用O(n)次。因此该规约的主要问题是证明addGadget函数的复杂性。
引理3函数addGadget每次执行时间最多为O(nc),c为常数,即多项式时间。
证明:显然,在addGadget中的循环开始前,最多添加了O(nc1)个比特,c1为常数,主要问题是循环迭代多少次才能结束。
在循环中,不断将当前的变量零件往纵坐标正向移动。其余的子句零件也沿着其固有的方向移动。例如子句x∨y,假设已经添加了x变量零件,正在添加y变量零件,那么该子句零件正沿着代表x取“真”的划分线向纵向的正向移动。各个点的移动速度不同。
当前最多有O(nc2)个相邻异色顶点对,c2为常数,2个相邻异色顶点对所确定的直线数目为O(n2c2),2条直线最多相交一次,一个零件一条直线上移动最多需要O(n3c2)次就能保证当前没有零件相互影响。所以循环在多项式时间内就能解决所有冲突并结束。
4 近似算法
将这个问题的最优化版本通过L归约,归约到Setcover问题。Setcover问题已知有近似比为O(lg(n))的近似算法[10]。
引理4多色点集直线划分问题能够在多项式时间内归约到Setcover问题。
证明:给定一个多色点集直线划分的实例。对于任意2个平面上的不同颜色的点pi,pj(i<j),构造一个元素aij,S是这些元素的集合。对于任意可行的直线lk,构造一个S的子集Ak,这个集合包含代表这条直线所划分的不同颜色点对的元素。总共有多项式个不同颜色的点对,多项式条可能的直线,每条直线划分多项式个不同颜色的点对,所以这个构造过程是多项式时间的。
引理5 这个归约是L归约。
证明:函数R是一个直线到子集的映射,S是一个子集到直线的映射,能够在对数空间内计算。且满足:

所以其为L归约。
根据L规约的性质,得到下面的定理:
定理2多色点集直线划分有多项式时间的O(lg(n))-近似算法。
算法2O(lg(n))-近似算法

每次迭代查找有O(n2)条直线,最多可以迭代O(n2)次,因此算法复杂度为O(n4)。
5 结束语
本文给出了多色点集直线划分问题的NP完全的复杂性证明,并且提出了一个多项式时间的O(lg(n))近似算法。该划分相较多边形的划分,对于解有更好的理论保证,可以较好地划分多色点集。在对于复杂性的证明中,只用到了2种颜色,这说明该问题极有可能不存在固定参数[11],至少颜色个数不是一个合适的参数。研究该问题在固定参数可解方面的复杂性是该问题的一个重要方向。另一方面,算法的时间复杂度仍然比较高,且没有完全利用平面的性质,下一步方向是尝试构造平面的Voronoi图[12],然后在近似算法中加入分治法来降低复杂度。
[1] Brass P,Moser W O J,Pach J.Research Problems in Discrete Geometry[M].[S.l.]:Springer,2005.
[2] Kaneko A,Kano M.Discrete Geometry on Red and Blue Points in the Plane Lattice[M].Berlin,Germany: Springer,2003.
[3] Ding Ren,Hosono K,Urabe M,et al.Partitioning a Planar Point Set into Empty Convex Polygons[C]// ProceedingsofConferenceonDiscreteand Computational Geometry.Berlin,Germany:Springer, 2003:129-134.
[4] Rosenfeld A.Picture Processing by Computer[J].ACM Computing Surveys,1969,1(3):147-176.
[5] Dumitrescu A,Kaye R.Matching Colored Points in the Plane:Some New Results[J].Computational Geometry, 2001,19(1):69-85.
[6] Atienza M N,Cortés C,Garijo D,et al.k-Factores en NubesBicromáticas[C]//ProceedingsofXII Encuentros de Geometria Computacional.Valladolid, Spain:[s.n.],2007:53-57.
[7] Dumitrescu A,Pach J.Partitioning Colored Point Sets into Monochromatic Parts[J].International Journal of Computational Geometry&Applications,2002,12(5): 401-412.
[8] 堵丁柱,葛可一,胡晓东.近似算法的设计与分析[M].北京:高等教育出版社,2011.
[9] Papadimitriou C H.Computational Complexity[M]. [S.l.]:Addison-Wesley,1993.
[10] Cormen T H,Leiserson C E.算法导论[M].2版.北京:机械工业出版社,2006.
[11] Cai Liming,Chen J.On Fixed-parameter Tractability and Approximability of NP Optimization Problems[J]. Journal of Computer and System Sciences,1997,54(3): 465-474.
[12] Aurenhammer F.Voronoi Diagrams——A Survey of a FundamentalGeometricDataStructure[J].ACM Computing Surveys,1991,23(3):345-405.
编辑 顾逸斐
Complexity of Multi-colored Point Set Partition with Straight Line and Its Approximation Algorithm
CHEN Chongchen,Rudolf Fleischer
(School of Computer Science,Fudan University,Shanghai 201203,China)
Partitioning multi-colored point set into monochromatic parts is an optimization problem in computational geometry.It focuses on how to dissect the plan with polychrome points into regions with monochrome points.But the approach of partitioning with polygon cannot get good partition results now.This paper comes up with an approach of partitioning with straight line.This problem is discredited to prove that non-deterministic turing machine can decide this problem.It reduces Max2SAT problem to this problem in polynomial time,and proves that it is NP-hard.Then multicolored point set is partitioned into monochromatic parts problem with straight line in NP-complete class.It gives an approximation algorithm for the optimization version by usingL-reduction from Setcover problem,and proves the approximation ratio isO(lgn).
computationalgeometry;computationalcomplexity;approximationalgorithm;partitionalgorithm; combinational optimization;NP complete
陈崇琛,Rudolf Fleischer.多色点集直线划分的复杂性及其近似算法[J].计算机工程,2015,41(2): 298-302.
英文引用格式:Chen Chongchen,Rudolf Fleische.Complexity of Multi-colored Point Set Partition with Straight Line and Its Approximation Algorithm[J].Computer Engineering,2015,41(2):298-302.
1000-3428(2015)02-0298-05
:A
:TP301.6
10.3969/j.issn.1000-3428.2015.02.057
上海市重点学科建设基金资助项目(B114);上海市科委科技基金资助项目(08DZ2271800,09DZ2272800)。
陈崇琛(1989-),男,硕士研究生,主研方向:计算几何,计算复杂性;Rudolf Fleischer,教授。
2014-03-21
:2014-04-14E-mail:chenkov@yeah.net
