使用中国剩余定理的群签名方案

党佳莉,俞惠芳

(青海师范大学计算机学院,西宁810008)

使用中国剩余定理的群签名方案

党佳莉,俞惠芳

(青海师范大学计算机学院,西宁810008)

现有群签名方案存在不能抵抗陷害攻击和伪造攻击的问题。为此,将中国剩余定理用于群签名中,提出一种新的群签名方案。利用中国剩余定理的数学特性,只需简单计算就能将一些重要的秘密信息进行整合,可以更好地保证成员私钥和身份的隐密性,同时,能够较好地控制计算过程中数据的长度,从而简化计算过程,在不改变其他合法群成员密钥的情况下,实现群成员的加入和撤销。分析结果表明,该方案具有匿名性、防伪造性、可跟踪性、防联合攻击和防重放攻击等优点。

数字签名;群签名;中国剩余定理;有限域;离散对数

1 概述

数字签名主要用来实现数据完整性和不可抵赖性。随着计算机技术的普及和电子通信技术的发展,面对各种各样的应用背景,需要不同的签名方案,因此,群签名思想应运而生。群签名是由文献[1]提出的。后来,研究者们对此进行了修改和完善。群签名方案允许任何一个群成员代表整个群体对消息进行签名,在出现争议时,则由群管理员来确定签名人的身份。同其他数字签名一样,群公钥能够对群签名进行公开验证。

1995年,文献[2]提出新的群签名方案,并提出在群签名方案中给群体增加新的群成员。2000年,文献[3]提出在群签名方案中可以撤销群成员。

尽管文献[2-3]方案是安全的,但在每次增加或撤销一个成员时需要做大量的指数运算,带来额外的繁重开销。近年来,人们又相继提出基于RSA[4]、离散对数[5]、椭圆曲线[6]、双线性对[7]等的群签名以及无证书群签名[8],使得群签名方案逐渐多样化。因为群签名在电子投票[9]、电子现金[10]等实际问题中具有广泛的应用,所以引起许多研究者的关注。

基于中国剩余定理的群签名方案由文献[11]于2004年提出,该方案不能防止陷害攻击。后来虽然经历了一些改进,但仍存在不少问题或缺陷,如文献[12]方案在防止伪造攻击和防止陷害攻击方面存在不足;文献[13]提出的群签名方案不能有效防止伪造攻击和联合攻击。

以上述内容为基础,本文提出一种使用中国剩余定理的群签名方案。给出群签名的定义、安全性要求以及中国剩余定理的介绍,并讨论方案的安全性。

2 预备知识

2.1 群签名

一个普通的群签名方案[14]可以通过以下概率多项式算法来定义,具体描述如下:

(1)建立:群中心用于产生群公钥、群成员及群管理员的密钥的算法。

(2)加入:用户和群管理员之间的使用户成为群管理员的交互式协议。执行该协议可以产生群成员的私钥和成员证书,并使群管理员得到群成员的私有密钥。

(3)撤销:用来撤销群成员的算法。

(4)签名:通过签名算法及群成员的签名密钥,对输入的消息进行签名。

(5)验证:通过验证算法,确定对输入消息的签名是否有效。

(6)打开:给定签名及群私钥的条件下确定签名者身份的算法。

2.2 群签名的安全性

群签名的安全性[11]从以下方面描述:

(1)匿名性:对于给定的群签名,除群管理员外,任何人想要确定签名者的身份在计算上是困难的。

(2)防伪造性:只有合法的群成员才能产生有效的群签名。

(3)可跟踪性:当签名出现争议的时候,群管理员可以打开一个签名,由此确定签名者的身份,而签名者不能阻止一个合法签名的打开。

(4)防陷害攻击:任何成员及群管理员都不能以其他成员的名义产生合法的群签名。

(5)抗联合攻击:群组中的成员不能联合产生一个合法的不可被跟踪的群签名。

(6)不可关联性:除群管理员外,任何人想判断2个或2个以上的消息是否由同一个成员产生是困难的。

2.3 中国剩余定理

设p1,p2,…,pk是k个两两互素的正整数,则对任意的整数y1,y2,…,yk,同余式[11]:

一定有解,且解是唯一的。令:

P=p1p2…pk,P=piPi,i=1,2,…,k则同余式组的解可表示为:

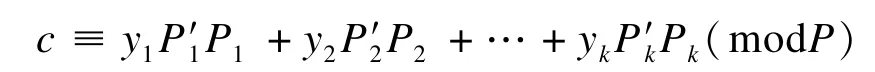
其中,P′iPi≡1(modpi),i=1,2,…,k。

3 本文群签名方案

3.1 系统的建立

已知安全参数k,群中心选择2个大素数:p′和q′,满足p=2p′+1,q=2q′+1,则p和q为安全素数,并计算n=pq。然后,群中心随机选择,计算y≡gx(modp)。接着,群中心定义一个抗碰撞的哈希函数:h:{0,1}∗→{0,1}k,(k=160 bit)。循环群和的生成元gp和gq,构造如下同余方程组:

易知g的阶为λ(n)=lcm(p-1,q-1),由g生成的群＜g＞是群中阶数最大的循环子群。群中心根据中国剩余定理计算g并将其公开。

群中心将(x,p,g)作为群中心的私钥,而y是群中心的公钥。

假设系统中有k个群成员。利用中国剩余定理,能够求出同余方程组c≡yi(modpi),i=1,2,…,k的解为:

其中,P,P′i,Pi如2.2节所述。将(n,y,g,c)作为群公钥发布。

3.2 群成员的加入

假设Alice向群中心提出申请,想成为群中心的一个成员,则需要以下步骤:

(2)重新计算:

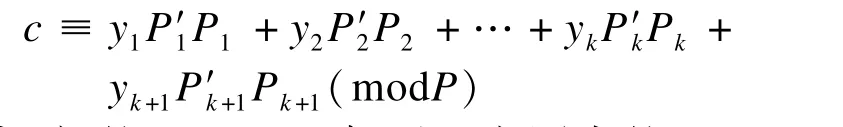
其中,新的P,P′i,Pi都可以由原来的P,P′i,Pi给出,即:

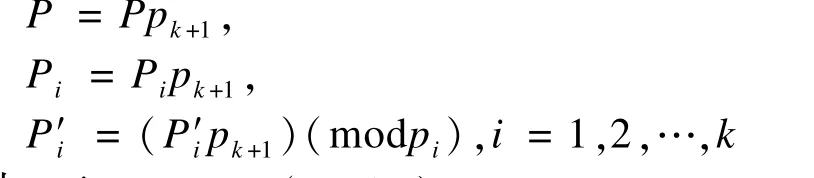
其中,P′k+1Pk+1≡1(modpi)。

(3)群中心重新发布新的c,然后将(IDk+1,yk+1)发送给群管理员。则Alice成为群中心的一个新成员,此时群中心其他有效成员的签名密钥并不发生改变,群公钥中只有c发生改变,但群公钥的个数并不改变。

3.3 群成员的撤销

设群中心有k个成员,并且:

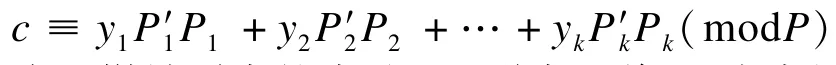
为了撤销群中的成员Ui,群中心将yi改成另外的一个随机数并且重新计算并发布新的c:

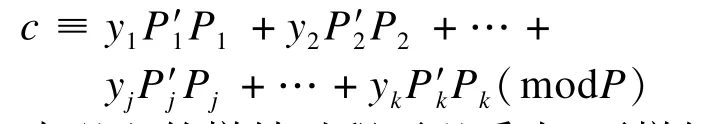
由以上的撤销过程可以看出,要撤销群中心的一个群成员,只需要改变c的值和进行一些简单的计算,由于P固定不变,c的长度也是不变的,因此整个群中心公钥的长度也不变。对于其他合法的群成员,此时,并不需要更新自身的签名密钥。因此,以上的撤销过程,无论对群中心还是群成员都是简单和高效的。

3.4 签名的生成

设群成员Ui要对消息m签名。选择一个随机数,计算。群成员Ui利用私钥xi对消息m签名,计算:

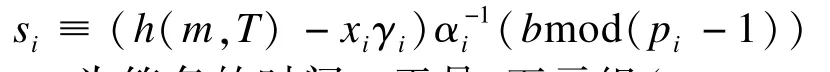
其中,T为签名的时间。于是,五元组(m,γi,si,pi,T)即为成员Ui对m的签名。

3.5 签名的验证

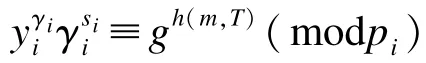
计算yi≡c(modpi),进而由(IDi,yi)确定签名者的身份。

4 安全性分析

4.1 防伪造攻击分析

定理1 假设Alice是合法群成员,攻击者截获了pA,要伪造Alice的签名(m,γA,sA,pA,T)在计算上是困难的。

证明:可以根据攻击者的身份分为以下2种情况来进行讨论:

(1)攻击者不是群成员

由于攻击者截获了pA,因此可以计算出yA≡c(bmodpA)。由于yA≡gxA(modpA),要求解xA等价于求解有限域上的离散对数问题,而这个问题是个难解问题。

(2)攻击者是合法群成员

攻击者利用自己的私钥xB和截获的pA,对消息m进行签名:

攻击者伪造的签名为(m,γB,sB,pA,T),验证者接收到签名后计算:

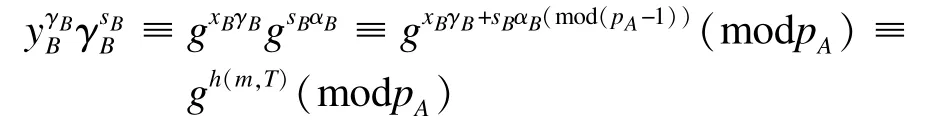
并通过验证。

则yA≡yB≡c(modpA),即:

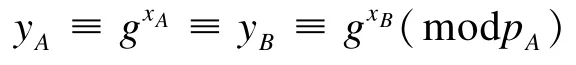
定理得证。

4.2 防陷害攻击分析

定理2 假设Bob是合法群成员,攻击者(群成员或者群管理员)即使截获了pB想要以Bob的名义生成对消息m的合法签名(m,γB,sB,pB,T)在计算上是困难的。

证明:利用反证法进行证明。

假设攻击者能够以Bob的名义生成对消息m的合法签名(m,γB,sB,pB,T)。

由于攻击者截获了pB,因此可以计算出yB≡c(modpB)。又因为:

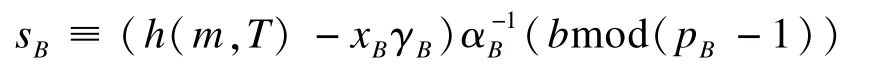
要计算xB必须通过yB≡gxB(modpB)来计算,等价于求解有限域上的离散对数问题,因此,在计算上是困难的。

定理得证。

4.3 防联合攻击分析

定理3 假设群中共有k+1个成员,即使其中的k个成员联合,想要求出第k+1个成员的密钥(xk+1,yk+1,pk+1)在计算上是困难的。

证明:利用反证法进行证明。

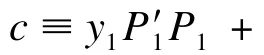
即已知yk+1和pk+1,求xk+1。攻击者可以执行以下操作:

(2)随机选择xi,yi,其中,yi≡gxi(modpi),i= 1,2,…,k。

(3)利用中国剩余定理计算:

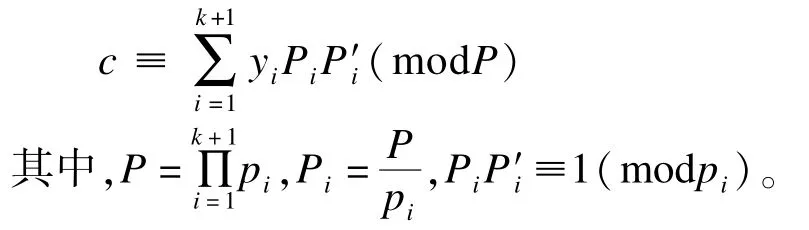
(4)将c,pi,yi(i,j=1,2,…,k+1)和xj,j=1, 2,…,k作为算法φ的输入,可以得到一组新的密钥对(xk+1,yk+1,pk+1)。

因此,攻击者通过以上步骤成功求解了有限域上的离散对数问题。

定理得证。

4.4 可跟踪性

定理4假设群成员Uj可以对消息m进行签名,且不被群管理员跟踪,则签名不成立。

证明:利用反证法进行证明。

假设Uj对消息m的签名为(m,γj,sj,pj,T)而且签名成立,则可以计算出群成员Uj的公钥yj≡c(modpj)

由于在系统建立时,群中心将每一个群成员的(IDi,yi),i=1,2,…,k发送给了群管理员,因此群管理员可以根据群公钥yj追踪到IDi,即可以追踪到签名的群成员。

定理得证。

4.5 防重放攻击和匿名性分析

该方案加入时间标志T,接受者收到签名后,计算接收时间与签名时间的时间差,如果超过规定的时间,则拒绝签名。因此,该方案可以防止重放攻击。

除群管理员以外,任何人根据签名者的公共信息确定签名者的身份在计算上都是困难的。因此,该方案可以保证群签名的匿名性。

5 效率分析

通过表1对本文方案和文献[11-13]进行了指数运算次数的比较,总运算次数依次为4次、7次、8次和7次。

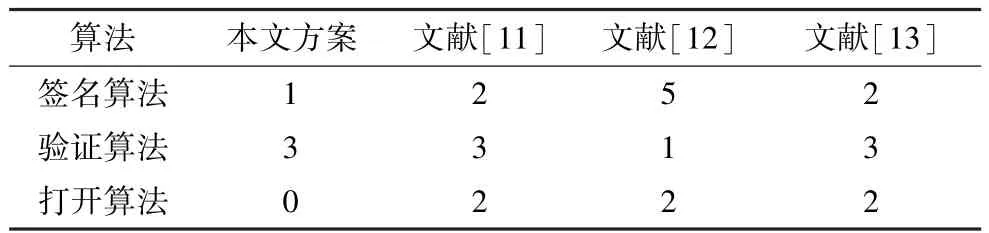
表1 4种方案运行不同算法时指数运算次数的比较

通过表2对本文方案和文献[11-13]的性能进行了比较,其中,“√”表示方案有此性能;“×”表示方案无此性能。

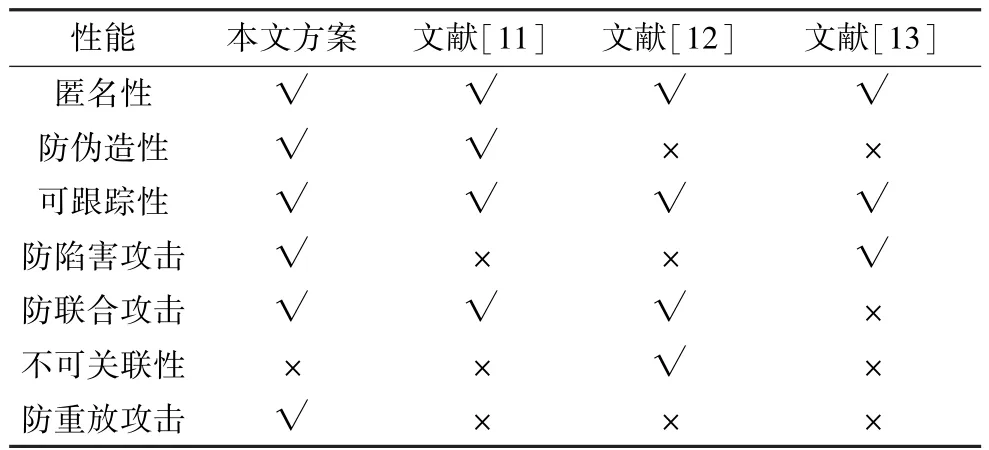
表2 不同方案的性能对比

分析表1和表2可知,本文方案的计算效率比文献[11-13]更高,而且性能也更完善。

6 结束语

本文提出一种使用中国剩余定理的群签名方案。该方案在不改变其他有效群成员密钥的同时,加入时间参数,在防止重放攻击方面具有明显优势。分析结果表明,该方案可以安全高效地实现群成员的加入和撤销,且效率较高。下一步将构建使用中国剩余定理的群盲签名方案。

[1] Chaum D,Heyst V E.Group Signatures[C]//Proceedings of EUROCRYPT’91.Berlin,Germany:Springer-Verlag, 1991:257-265.

[2] Chen L,Pedersen T.New Group Signature Schemes[C]// ProceedingsofEUROCRYPT’94.Berlin,Germany: Springer-Verlag,1995:171-181.

[3] Kim H,Lim J,Lee D.Efficient and Secure Member Deletion in Group Signature Schemes[C]//Proceedings of the 3rd International Conference on Information Security and Cryptology.Berlin,Germany:Springer-Verlag,2000:150-161.

[4] 李凤银,禹继国,鞠宏伟.一种基于RSA的群签名[J].计算机工程与设计,2006,27(16):2955-2957.

[5] 徐光宝,张建中.一种基于离散对数的群签名方案[J].计算机工程,2005,31(9):143-144.

[6] 谢 冬,李佳佳,沈忠华.一种新的基于椭圆曲线的门限群签名方案[J].杭州师范大学学报:自然科学版, 2013,12(1):57-60.

[7] 袁 艳.基于双线性对的数字签名的研究与设计[D].武汉:湖北工业大学,2011.

[8] 陈 虎,宋如顺.无证书群签名方案[J].计算机工程, 2009,35(9):130-132.

[9] 乔汇东,胡 瑛.基于群签名的电子投票方案[J].湖南工程学院学报:自然科学版,2012,22(4):23-27.

[10] 王凤和.群签名及其在电子现金中的应用研究[D].西安:西安电子科技大学,2006.

[11] 陈泽文,张龙军,王育民,等.一种基于中国剩余定理的群签名方案[J].电子学报,2004,32(7):1062-1065.

[12] 胡 斌,施荣华,娄 悦.一种改进的基于中国剩余定理的群签名方案[J].计算机工程与应用,2006, 42(24):115-117.

[13] 李 俊,崔国华,刘志远.一个群签名方案的密码学分析与改进[J].电子学报,2007,35(4):778-781.

[14] 鞠宏伟.3类新型的数字签名方案研究[D].济南:山东师范大学,2005.

编辑 刘 冰

Group Signature Scheme Using Chinese Remainder Theorem

DANG Jiali,YU Huifang
(School of Computer,Qinghai Normal University,Xining 810008,China)

Some existing group signatures can not resist the defects of exculpability and unforgeability.In order to solve this problem,this paper applies the Chinese remainder theorem to group signature,and proposes a secure group signature scheme using Chinese remainder theorem.Using the mathematical properties of Chinese remainder theorem,only simple calculation to some important secret information integration can better ensure the privacy of the private key and identity. At the same time,this scheme can effectively control the length of the data in the process of calculation,thus,it simplifies the process of calculation.Under not changing the secret key of other group member,the group member can be added or revoked efficiently.Analysis results show that this scheme has anonymity,unforgeability,traceability,coalition-resistance and coalition-replay attacks.

digital signature;group signature;Chinese remainder theorem;finite field;discrete logarithm

党佳莉,俞惠芳.使用中国剩余定理的群签名方案[J].计算机工程,2015,41(2):113-116.

英文引用格式:Dang Jiali,Yu Huifang.Group Signature Scheme Using Chinese Remainder Theorem[J].Computer Engineering,2015,41(2):113-116.

1000-3428(2015)02-0113-04

:A

:TP309

10.3969/j.issn.1000-3428.2015.02.022

国家自然科学基金资助项目(61363080);教育部春晖计划基金资助项目(Z2012094)。

党佳莉(1988-),女,硕士研究生,主研方向:密码学,信息安全;俞惠芳,副教授、博士研究生。

2014-03-28

:2014-04-23E-mail:yuhuifang@qhnu.edu.cn