基于多变量公钥密码体制的环签名变体方案

刘筱茜,赵一鸣

(复旦大学软件学院,上海201203)

基于多变量公钥密码体制的环签名变体方案

刘筱茜,赵一鸣

(复旦大学软件学院,上海201203)

基于多元二次方(MQ)问题的多变量公钥密码体制是一种可以抵抗量子攻击的系统。分析基于多变量公钥密码体制的环签名方案,指出其存在密钥泄露和安全证明错误的问题。为解决上述问题,对环签名者和其他环成员采用不同的密钥构造方式,提出一种可证明安全的环签名变体方案。该方案最大程度地去除原方案对IP问题的依赖,使得方案的安全性直接规约于MQ问题,以提升安全性。在环签名的标准安全模型下,分别从正确性、匿名性和不可伪造性等方面对方案进行分析和安全性证明,结果表明,与原方案相比,该方案有较高的安全性。

多变量公钥密码体制;多元二次方问题;IP问题;密钥泄露;环签名;可证明安全

1 概述

量子计算机的发展对目前现有的公钥密码体制构成了潜在的威胁,1994年Shor量子算法[1]的提出使得量子计算机能以多项式时间攻击现有的基于大素数分解和离散对数难题,因此,在量子计算机环境下,需要为基于这些问题的签名方案提供备选方案。目前,被认为能够抵抗量子计算攻击的方案主要基于编码、格和MQ问题,其中基于MQ问题构造的方案由于占用资源较少的特点,适用于低消耗的设备,如RFID芯片、智能卡等移动设备上。

另一方面,在传统密码学中有许多不同的签名方案设计,如代理签名、盲签名等,适用于不同情形,其中包括环签名。环签名由Rivest等人于2001年提出[2],非常适用于消息的匿名发布等应用场景,之后文献[3]提出基于双线性对的环签名。环签名不仅在传统密码学中,而且在量子计算环境下的应用也具有很大研究意义。

本文主要分析文献[4]中基于MPKC的签名方案,指出其存在私钥泄露问题和安全性分析问题,然后给出分析过程、改进方案,以及新方案的可证明安全。

2 预备知识

2.1 MQ问题

定义1 给定一个有限域GF(q)上m个多项式n个变量的随机多变量二次多项式组p(1),p(2),…,p(m),求解一个向量x=(x1,x2,…,xn)∈GF(q)n,满足p(1)(x)=…=p(m)(x)=0。

MQ问题在文献[5]中被证明是NP难解问题,即使是在仅有2个元素的有限域GF(2)上仍是难解问题。

2.2 MPKC方案

基于MQ问题的多变量公钥加密体系(MPKC)是在有限域GF(q)上构建的多变量二次方程式系统,其中有m个多项式n个变量,每个多项式的形式为:

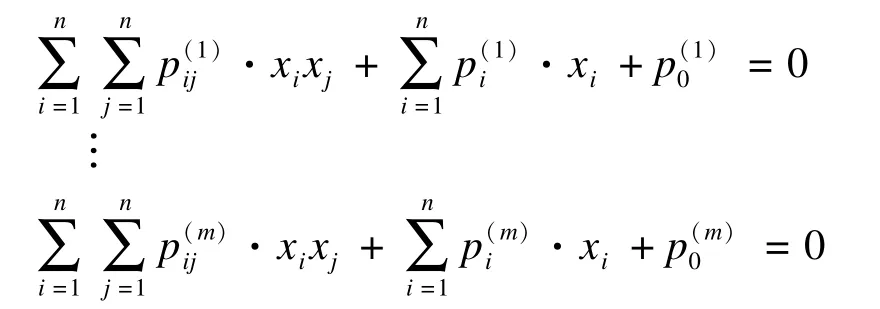
现有的大多数MPKC方案中公钥系数并非随机选取,而是由可逆二次中心映射F和为了隐藏F的可逆仿射变换L和R来构建公钥P=L°F°R,因此,这些方案的安全性不仅基于MQ问题,还基于IP问题。

2.3 IP问题

定义2 假设P和F是2个给定的有限域GF(q)上m个多项式n个变量的随机多变量二次多项式组,求解有限域GF(q)上的2个仿射变换L∈GF(q)n×GF(q)n和R∈GF(q)m×GF(q)m,且P=L°F°R。

引入仿射变换L和R来隐藏中心映射F构建公钥P=L°F°R是为了让合法用户能够容易解密密文,从而构建单向陷门函数,在此情况下P和F是同构的。已知P和F求解仿射变换L和R的问题称为多项式同构问题,即IP(Isomorphism of Polynomials)问题,该问题已被证明为一个NP困难性问题[6]。

2.4 环签名方案

在环签名方案中,签名者选择一个包括自己在内的一个群组,用自己的私钥和其他环成员的公钥对消息进行签名。验证者可以验证消息的确来自该环中成员的签名,但是不能指出具体签名者。环签名方案一般包括:系数生成,密钥生成,签名生成,签名验证,最终满足完整性、匿名性和不可伪造性。完整性:根据给出的环签名和环成员公钥信息能够成功验证签名;匿名性:任意2个环成员生成的环签名对攻击者来说是不可区分的;不可伪造性:攻击者成功伪造环签名的概率是可忽略的。

3 MQ环签名方案分析

3.1 基于MPKC的环签名方案

MPKC的环签名方案过程如下:

(1)系统建立(Setup)

生成系统参数(k,q,p,l,m,n,H),其中,k=GF(q)是特征为p的有限域;q=pl;l为正整数;m是多变量方程组的个数;H是变量的个数且m和n均为正整数。哈希函数H:{0,1}∗→km,Pi(i=1, 2,…,r)是第i个环成员的公钥,Pi=Li°Fi°Ri,其中,Li,Fi,Ri是该用户的私钥。

(2)密钥生成(KGen)

环中每个成员的公私钥对生成为(PKi,SKi),i=1,2,…,r。PKi:Pi=Li°Fi°Ri,SKi:Li,Fi,Ri,其中,Li,Ri分别是从km到km和kn到kn随机选取的可逆仿射变换,Fi是有限域k=GF(q)上可逆的二次多变量方程的中心映射。

(3)签名生成(PSign)

环成员U(u1,u2,…,ur)所对应的公钥集合为(P1,P2,…,Pr),现有一名环成员us代表整个环成员对消息进行签名,签名者us的私钥为SKi:Ls,Fs,Rs,对消息m进行如下签名操作:

首先,对除签名者us外的所有环成员,随机选取2个n维向量ai∈kn和kn(i=1,2,…,r,i≠s),令:

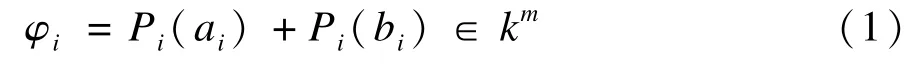
然后,对签名者us随机选取一个n维向量φs∈kn,并计算:

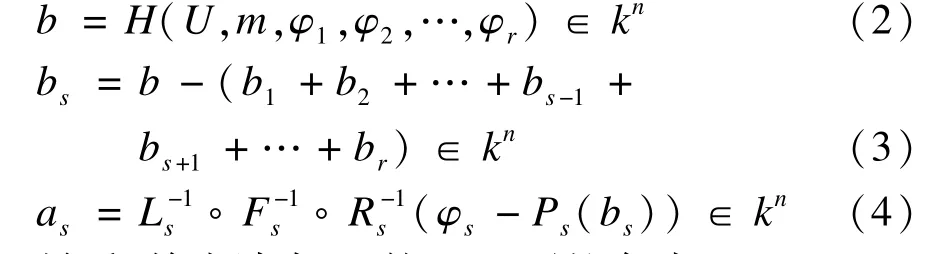
最后,给出消息m的MQ环签名为δ=(U,a1,b1,…,ar,br)。

(4)签名验证(Verify)

已知环成员集合U(u1,u2,…,ur),对应的公钥集合(P1,P2,…,Pr),对消息m产生的签名δ=(U,a1,b1,…,ar,br),验证者检验以下等式是否成立:

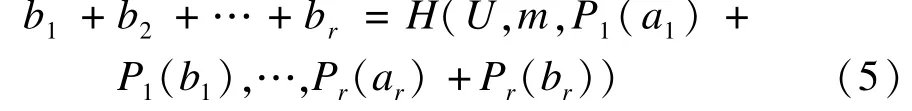
若式(5)成立,那么验证者接受该签名,否则拒绝该签名。

3.2 存在问题

分析文献[6]的方案,存在以下2个问题: (1)整个方案进行安全性分析前没有考虑私钥泄露问题;(2)该方案是基于MPKC方案生成,非直接规约于MQ难解问题,安全性说明没有说服力。

针对文献[6]存在的问题,下面分别进行相应分析及给出解决方案。

(1)私钥泄露

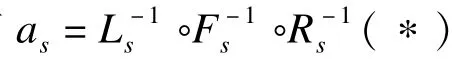
为了保证方案不泄露私钥,则要使得环成员us的签名方案是基于MQ问题的安全签名方案,所以有以下定理:

根据文献[7]可知,目前基于MQ问题的签名方案被指出只有UOV,Rainbow,Enhanced TTS等几种尚未被攻破的安全签名方案,选取其中一种作为环签名者us用自己私钥进行签名得到as的安全签名方案,并选取其对应的安全参数系数。

(2)基于MQ难解问题

文献[6]的方案中,r个环成员均以P=L°F°R来构造公私钥对,随后说明其基于MPKC方案的安全性。然而,如此构造的方案并非是直接基于MQ问题的签名方案,而是结合了IP问题从而加入了陷门函数,使得方案易于转置,具有较大的不安全性,如文献[7-10]均为已被攻破方案,并且文献[11]中指出大部分MPKC方案采用此构造方式均已破解,所以需要构建直接基于MQ问题的环签名方案以保证方案的安全性。

根据上一节中选定环签名者us的安全签名方案后,确定环U中其他环成员(u1,u2,…,us-1,us+1,…,ur)的公私钥构建方案应为仅基于MQ问题的MPKC方案。

4 变体方案

为避免私钥泄露和提升方案安全性,下面对原方案的系统建立和密钥生产进行改进:

(1)系统建立(Setup)

生成系统参数(k,q,p,l,m,n,H),其中,k=GF(q)是特征为p的有限域;q=pl且为奇素数;l为正整数;m是多变量方程组的个数;n是变量的个数且m和n均为正整数。哈希函数H:{0,1}∗→km。

(2)密钥生成(KGen)

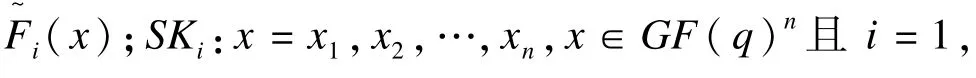
签名生成和签名验证和原方案一致。如此构造的新方案不仅降低了原方案不安全的风险,而且满足文献[12]中对(x)分布是伪随机分布的分析定理。

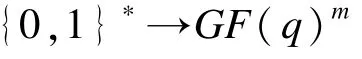
5 可证明安全

根据环签名方案模型设计,MQ环签名方案应当同时满足完整性、匿名性和不可伪造性,下面对新方案进行分别证明。

5.1 完整性

严格按照方案进行签名,并且在传输过程中没有改变,那么验证者可知对消息m的签名δ=(U,a1,b1,…,ar,br),环成员U(u1,u2,…,ur)以及他们的公钥PKi,i=1,2,…,r。验证等式(6):

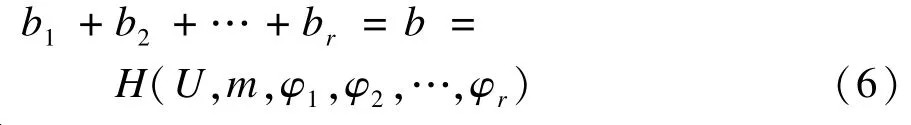
其中,φi=Pi(ai)+Pi(bi),那么代入ai,bi容易验证等式(6)成立,即新方案满足完整性。

5.2 匿名性

为了证明新方案的匿名性,下面分析U(u1,u2,…,ur)中任意2个环成员uj,uk生成的签名δj,δk是不可区分的。

定理3 环H(U,m,φ1,φ2,…,φr)中任意环成员ue(e=1,2,…,r)对消息m生成的MQ环签名δe=(U,a1,b1,…,ae,be,…,ar,br)满足伪随机分布。

由新MQ环签名设计方案可知,a1,a2,…,ae-1,ae+1,…,ar和b1,…,be-1,be+1,…,br是从有限域GF(q)n中随机选取的。分析be=b-(b1+b2+…+be-1+be+1+…+br)。其中,b=H(U,m,φ1,φ2,…,φr)满足伪随机分布,所以be亦满足伪随机分布。再分析ae=L-1e°F-1e°R-1e(φe-Pe(be)),由于φe是在有限域GF(q)n上随机选取的n维向量,因此φe-Pe(be)满足伪随机分布,同时在新方案中ae是采用基于MQ问题的安全签名方案如Rainbow,签名满足伪随机性。综上所述,环中任意成员ue生成的MQ环签名δe=(U,a1,b1,…,ae,be,…,ar,br)满足伪随机性。

根据定理3可知,任意2个环成员uj,uk的签名δj,δk均为伪随机分布,那么满足不可区分性,从而验证了新方案的匿名性成立。

5.3 不可伪造性

将等式(6)变形为b=H(U,m,θ),其中,θ:P1(a1)+P1(b1),…,Pr(ar)+Pr(br)。

假设:签名δ′(U,a′1,b′1,…,a′r,b′r)是攻击者成功伪造的对消息m的一个能够通过验证的MQ环签名。

同时,实际签名者us通过新的签名方案得到真实签名δ(U,a1,b1,…,ar,br)。由于δ和δ’都能通过认证,有以下等式成立:

情形1 若b≠b′,由式(7)、式(8)可知,H(U,m,θ)≠H(U,m,θ′),那么对于b′攻击者找到了在哈希函数H(U,m,θ′)的一个原象,其中,θ′是伪造签名的一部分,其余为公开的环成员集合U和消息m。

情形2 若b=b′,则H(U,m,θ)=H(U,m,θ′)那么θ=θ′,即P1(a1)+P1(b1)=P1(a′1)+P1(b′1),…,Pr(ar)+Pr(br)=Pr(a′r)+Pr(b′r)其中,Pi是环成员i的公钥,ai,a′i,bi,b′i∈kn为随机选取的n维向量,根据定理2可知,Pi(ai),Pi(a′i),Pi(bi),Pi(b′i)均为伪随机分布,则Pi(ai)+Pi(bi)和Pi(a′i)+Pi(b′i)也均为伪随机分布,且不可区分,从而得出攻击者成功破解了MQ问题,这与MQ问题是难解问题相矛盾。

6 结束语

本文针对基于多变量公钥密码体制的环签名方案进行分析,指出其存在私钥泄露。针对上述问题,对该方案进行了改进,提出一种可证明安全的环签名变体方案,并给出完整的安全性证明,以MQ难解问题为基础,进行可证明安全分析,保证签名方案的正确性、匿名性和不可伪造性。本文方案在提高了原方案安全性的同时,还存在每次更换环签名者时,需重新生成环签名者的公私钥对,这是下一步需要研究的问题。

[1] Shor P W.AlgorithmsforQuantumComputation: Discrete Logarithms and Factoring[C]//Proceedings of the35thAnnualSymposiumonFoundationsof Computer Science.[S.1.]:IEEE Press,1994:124-134.

[2] Rivest R L,Shamir A,Tauman Y.How to Leak a Secret[M].Berlin,Germany:Springer,2001.

[3] Xu J,Zhang Z,Feng D.A Ring Signature Scheme Using Bilinear Pairings[M].Berlin,Germany:Springer,2005.

[4] 王晓兰.基于多变量公钥密码体制的环签名方案[J].河南科学,2013,(3):318-321.

[5] Johnson D S.TheNP-completenessColumn:An Ongoing Guide[J].Journal of Algorithms,1984,5(3): 433-447.

[6] Patarin J.HiddenFieldsEquations(HFE)and Isomorphisms of Polynomials(IP):Two New Families ofAsymmetricalgorithms[C]//Proceedingsof Eurocrypt’96.Berlin,Germany:Springer,1996:33-48.

[7] Bouillaguet C,Faugère J C,Fouque P A,et al.Practical Cryptanalysis of the Identification Scheme Based on the Isomorphism ofPolynomialwithOneSecretProblem[C]//Proceedings of PKC’11.Berlin,Germany: Springer,2011:473-493.

[8] Dubois V,Fouque P A,Shamir A,et al.Practical CryptanalysisofSFLASH[C]//Proceedingsof CRYPTO’07.Berlin,Germany:Springer,2007:1-12.

[9] Kipnis A,Shamir A.Cryptanalysis of the Oiland VinegarSignatureScheme[C]//Proceedingsof CRYPTO’98.Berlin,Germany:Springer,1998:257-266.

[10] Patarin J.Cryptanalysis of the Matsumoto and Imai Public Key Scheme[C]//Proceedings of CRYPTO’95. Berlin,Germany:Springer,1995:248-261.

[11] Thomae E.About the Security of Multivariate Quadratic Public Key Schemes[EB/OL].(2013-10-21).http:// www.cits.rub.de/personen/thomae.html.

[12] Huang Y J,LiuFH,YangBY.Public-key CryptographyfromNewMultivariateQuadratic assumptions[C]//Proceedings of PKC’12.Berlin, Germany:Springer,2012:190-205.

编辑 索书志

Variant Scheme of Ring Signature Based on Multivariate Public Key Cryptosystems

LIU Xiaoqian,ZHAO Yiming
(Software School,Fudan University,Shanghai 201203,China)

Based on Multivariate Quadratic(MQ)problem,Multivariate Public Key Cryptosystems(MPKC)are regarded as systems resisting quantum attacks.This paper analyzes a ring signature scheme based on MQ and points out that there exist some issues such as secret key leakage and incorrect security proof.To solve these problems,this paper proposes a variant of ring signature scheme with provable security by applying different key generation methods to ring signer and the remaining ring members.The scheme removes the dependence on IP problem as much as possible,gaining higher security by direct reduction to MQ problem.This paper gives detailed analysis and security proof of the new scheme from the aspects of correctness,anonymity and unforgeability in the standard security model of ring signature. Compared with the original scheme,the scheme is more complete both in analysis and security proof.

Multivariate Public Key Cryptosystems(MPKC);Multivariate Quadratic(MQ)problem;IP problem; secret key leakage;ring signature;provable security

刘筱茜,赵一鸣.基于多变量公钥密码体制的环签名变体方案[J].计算机工程,2015,41(2):96-99.

英文引用格式:Liu Xiaoqian,Zhao Yiming.Variant scheme of Ring Signature Based on Multivariate Public Key Cryptosystems[J].Computer Engineering,2015,41(2):96-99.

1000-3428(2015)02-0096-04

:A

:TP309

10.3969/j.issn.1000-3428.2015.02.019

国家“十二五”密码发展基金资助项目。

刘筱茜(1990-),女,硕士研究生,主研方向:密码学,信息安全;赵一鸣,副教授。

2014-04-02

:2014-05-06E-mail:11212010019@fudan.edu.cn