无线传感器网络中一种基于可靠性的数据收集算法

黄 媛

(1.西北大学信息科学与技术学院,西安710127;2.陕西省行政学院计算机应用系,西安710068)

无线传感器网络中一种基于可靠性的数据收集算法

黄 媛1,2

(1.西北大学信息科学与技术学院,西安710127;2.陕西省行政学院计算机应用系,西安710068)

为实现无线传感器网络数据的低延时、高可靠性收集,将数据收集时涉及到的收集树构建、链路调度与功率分配联合问题定义为一个使数据收集延时最小化的优化问题。将该问题分成2个子问题:低延时数据收集树的构建和针对数据收集树的链路调度与功率分配,并为每个子问题提供一种多项式启发算法。仿真结果表明,与现有数据收集策略相比,该算法的数据收集延时明显降低,且可靠性更高。

无线传感器网络;数据收集;链路调度;功率分配;SINR约束;延时;可靠性

1 概述

无线传感器网络[1](Wireless Sensor Network, WSN)是近年来受到国内外广泛关注的研究热点。无线传感器网络在工作过程中,节点会不断地感知到周边环境的数据,并通过无线天线将数据以多跳的方式发送给远方的Sink节点(或称为基站)进行处理,即数据收集[2]。数据收集是无线传感器网络中最重要的操作之一,能否有效地收集到合适的数据,直接关系到应用的效果。由于节点只有有限的能量以及有限的存储、计算和通信能力,如何使网络能长时间的工作并且在数据收集的过程中满足应用的需求,以解决节点能量耗费不平衡、数据收集延迟过大等问题,是目前数据收集中面临的主要挑战。

本文在已有研究工作的基础上,提出了一种兼顾时延和可靠性的数据收集算法。

2 相关工作

数据收集问题在无线传感器网络中已经被广泛研究,相继有众多研究者提出了一系列有代表性的方案。文献[3]研究了基于移动协助数据收集的无线传感器网络结构,分类总结了近年来提出的一些典型的基于移动收集者(MDC)的算法和协议,针对传感器网络中MDC的研究提出了亟待解决的问题,并展望了其未来的发展方向。文献[4]为了提高数据收集可靠性和延长网络生命周期,提出了基于多元簇首的分簇数据收集算法。算法将网络划分为大小相等的栅格,由每个栅格中的节点各自构成一个簇,根据节点失效概率从每个栅格中选出多个簇首,并由同一栅格中的多个簇首协作完成栅格中节点的数据收集任务。仿真结果表明,该算法具有较高的数据收集可靠性,并能够显著延长网络生命周期。文献[5]提出了一种能量均衡的基于连通支配集的分布式算法EBCDS来进行数据收集,通过选择能量水平和度均比较大的节点组成连通支配集,支配集中的节点组成一个规模不大但具有较高能量水平的网络骨干。网络中的所有数据沿骨干在较小的寻路空间中转发,能够节省节点能量,使骨干节点不会因为能量不足而过早死亡。理论分析表明,EBCDS能以O(nlogn)的消息复杂度构造连通支配集,仿真实验表明,EBCDS能有效节省节点能耗并延长网络生命周期。

文献[6]提出一种能量高效的数据收集算法(Energy-efficient Data Gathering Algorithm,EEDGA)。该算法利用移动代理模型在网络中进行数据收集。首先EEDGA根据监测精度的要求控制活动节点的数量;然后通过求最小支配集得到具体的工作节点;最后利用蚁群算法规划移动代理迁移的最优路线,移动代理以渐进方式收集活动节点的监测数据。文献[7]提出一种基于多信道的快速数据收集MAC协议,结合多信道和时分多址复用消除节点间的干扰,在节点进行时槽分配时充分考虑节点半双工通信方式和数据收集公平性,尽可能地在空间上实现信道的复用,提高数据传输的并行性。在时序调度过程中,引入网络时延能耗平衡因子,实现不同应用场合对时延和能耗的平衡调节,增强协议的灵活性。仿真结果表明,该协议在大规模数据收集应用中具有高吞吐量、低时延的特性。

3 问题定义

考虑由一组静态传感器节点构成的一个传感器网络,表示为N。网络中的Sink负责对来自其他节点的数据进行收集和处理。每个传感器节点从P=集合中选择一个发射功率进行无线通信。为了确保高可用性,链路接收端的SINR应该大于最小阈值λ。对任意2个节点i和j,当节点以pmax功率发射信号且无其他链路干扰,那么如果节点j的SINR大于λ,则从节点i到j存在一条有向链路。注意节点i和j的干扰和噪声水平是不对称的,所以链路(i,j)是有向的。本文使用集合L来表示网络中所有的有向链路。此外,定义K为即使每个时隙只有一个链路处于传输活跃状态,也足以将所有节点的报文传输给Sink的大量时隙。使用一个二元变量来表示链路(i,j)是否被安排在时间t内传输数据。如果,则表示在时隙t内,链路(i,j)是可以传输数据的活跃链路。有:

在上述定义中,式(2)和式(3)分别明确了所有节点的发射功率和流量需求范围。式(6)～式(8)和式(11)分别是数据收集、链路调度和SINR阈值约束[8];式(9)和式(10)分别用于确定每条链路的接收功率和SINR。表1给出了相关标记法。当获得最优解后,没有活跃链路的时隙就被删除,剩余时间隙形成时间帧。

表1 优化问题相关符号的含义

4 启发式算法

在上文定义的优化问题中,当传感器节点数量变多时,约束条件数量将呈指数上升,使得难以通过数学工具求得最优解。为了降低问题难度,将问题分为2个子问题:(1)构建一个低延时数据收集树; (2)调度链路,并在每个时隙为活跃链路分配发射功率,于是当所有活跃链路的SINR大于λ时实现数据收集时间最小化。首先引入基于功率的增强型冲突图,以降低这2个子问题的处理难度,然后为每个子问题提供一个启发式算法。

4.1 基于功率的增强型冲突图

文献[9]讨论了基于功率的冲突图,在该图中,已知任意功率分配方案后,如果2个顶点的对应链路在无线传感器网络中无法同时调度,则这2个顶点相连。该图可以帮助调度数据收集树的链路。然而,该图没有反映本文启发式算法需要的链路流量负载。因此,针对数据收集问题对该图进行拓展,形成基于功率的增强型冲突图,将该图定义为一个加权无向图I=(V,E,W),其中,V是顶点结合;E是表示冲突关系的边集合,W是所有顶点的权重集合。V中每个顶点关联数据收集树上的一个链路。顶点权重定义为关联链路的剩余流量负载。对2个顶点,如果它们的关联链路的流量负载为正,且无可行性功率分配方案使它们满足最小SINR阈值,或者它们共享一个节点,则这2个顶点相连。对2条链路,如果它们在I上的关联顶点相连,则这2条链路不相容。

4.2 数据收集树的构建

在LLHC算法中,通过宽度优先(BFS)搜索算法遍历整个网络,为每个节点分配一个高度。遍历时以Sink为起点,以使节点的高度等于节点到Sink的最短跳数。本文其余部分,词汇“高度”和“层”可以互用。此外,为网络构建一个基于功率的增强型冲突图I。数据收集树T在开始时为空。首先,高度为1的所有节点及其与Sink的有向链路被添加到T中。然后,每个下层节点被选为子树的根。于是,由于BFS的遍历特性,可知子树的数量实现了最大化。按照节点高度的升序,将所有其他节点加到树T中。高度为m的节点可以选择m-1层任意节点作为母节点,前提是它们之间存在一条有向链路。如上文所述,可以实现最大子树规模最小化且引入的新链路与T上大多数链路均兼容的节点应该被选为母节点。为母节点定义一个权重以反映这两方面因素。对节点i的母节点候选节点j,其权重定义为节点j隶属的子树规模和T中与链路(i,j)不兼容的链路数量之和。权重最小的候选节点j′将被选为节点i的母节点,且链路(i,j′)被加到T中。重复这一步骤,直到所有节点属于T。

每当有新节点加入到数据收集树时,由于节点数量有限,因此算法肯定会终止。LLHC算法的伪代码如下:

算法1LLHC算法

输入传感器节点集合N;有向链路集合L

输出数据收集树T

对N中所有节点,将发射功率初始化为pmax;

对N中所有节点,将母节点初始化为-1;

生成增强型功率(power)干扰矩阵I;

使用BFD算法遍历整个网络,获得所有节点的层次level(i);

从算法中可以看出,它生成基于功率的增强型冲突图和基于BFS算法遍历所有节点的耗时分别为和。假设节点有M层,每层m的节点数量为nm,于是有n1+n2+…+nm=。在最坏情况下,m-1层的任意节点均可以是m层每个节点的母节点。于是,如果假设确定母节点候选节点的权重的耗时恒定,则将m层节点连接到树T需要耗时O(nm-1·nm)。于是连接所有节点的时间为O(n1·n2+n2·n3+…+nM-1·nM)=。因此,LLHC算法的总体时间复杂度为:。

4.3 链路调度和功率分配

在用LLHC算法确定一个数据收集树后,下一步就是为树上的链路分配时隙和发射功率,以实现数据收集延时最小化。本文提出一种最大权重优先(MWF)算法进行链路的调度和发射功率的分配,在该算法中,链路的权重定义为该链路剩余流量负载和该链路在I上的关联顶点的度两者之和。

已知一组链路后,如何确定它们的发射机是否存在一种功率分配向量,以满足所有链路的SINR约束,是一大难题。由于冲突干扰的累加性,即使这些链路在冲突图上的关联顶点互相独立,也并不一定存在合适的功率分配方案。当链路数量较大时,野蛮搜索方法不具有可行性。对不存在共有节点的一组链路M,定义可行性矩阵如下:

其中,链路ms的发射机和接收机分别表示为mt和mr。可行性矩阵F的第(i,j)个元素定义为:

其中,g(jt,ir)表示链路j发射机到链路i接收机的信道增益;g(it,ir)是链路i的信道增益。

在MWF算法中,首先针对数据收集树T,构建基于功率的增强型冲突图I。然后,对T上的所有链路按照链路降序排列。分配一个新的时隙t,权重最大的链路m放入时隙t的活跃链路集合St。链路m的流量负载降1。检查具有第2高权重的链路m′和St中其他链路的兼容性。如果链路m′与所有链路兼容,则对链路St∪m′构建可行性矩阵F。如果可以为F找到一个可行的功率分配方案,则将链路m′加入到St中,同时m′的流量负载降1。否则,检查排序列表上的下一条链路。当具有剩余流量负载的所有链路一次检查完毕后,时隙t的活跃链路集合t也最终确定。此后,相应更新冲突图I。分配新的时隙t+1,重复这一步骤,直到T的所有链路的流量负载为0。

由于每个时隙中,至少一个链路被调度,而且总体流量负载有限,因此算法必然会终止。MWF算法的伪代码如下:

算法2MWF算法

输入数据收集树T;发射功率集合P;流量需求D

输出链路调度矩阵S,功率分配矩阵U

生成收集树T的基于功率的增强型冲突图I;

确定T上每条链路的流量负载;

为了分析MWF算法的时间复杂度,假设每个时隙内平均有u条链路被调度。在最坏情况下,排序链路列表中的前u条链路始终被选入活跃链路集合。然后对剩余的条链路中的每条链路,需要耗费O(u)时间来检查链路是否与前u条链路兼容。如果兼容,还需再耗费O((u+1)3)的时间来检查矩阵F的可行性,且计算n×n矩阵的特征值和特征向量需要时间O(n3)。否则,该链路不能加入活跃链路集合,进而检查下一条剩余链路的兼容性。在最坏情况下,所有传感器分散在一条直线上且Sink位于直线一端,于是数据收集树也有一个直线拓扑结构。这种情况的流量负载之和为1)/2。因此,需要的时隙数量为。 MWF算法的总时间复杂度近似为:

5 性能评估

本节通过仿真实验来评估LLHC和MWF算法的性能。首先研究不同节点密度和SINR阈值的情况下本文算法的有效性。然后考察数据收集负载在平均中继流量和节点最大缓存长度2个方面的分布情况。其次研究Sink位置对数据收集延时的影响。为便于比较,同时部署了宽度优先搜索算法(BFS)和最大寿命树算法(MLT),以生成数据收集树;综合调度和功率控制算法(ISPA)和增大需求贪婪调度(IDGS)算法[11]也被部署,以对数据收集树上的链路进行调度。在仿真中,节点随机分布于500 m× 500 m方形区域中。所有节点的最大发射功率为-10 dBm。此外,所有节点在5 MHz频段上通信,加性高斯白噪声的均值(AWGN)为-97 dBm。使用长距离路径损耗模型作为传播模型,其中,路径损耗指数为3,Xδ的标准差为7 dB。除非另外指定,否则,SINR的最小阈值为10 dB且Sink部署于区域中央。所有结果运行100次取均值。

首先评估LLHC和MWF算法在数据收集所需的时隙数量方面的性能。传感器节点的数量范围为50～200,以25为步进量。仿真结果见图1(a),在图中,LLHC和MWF联合运行,而BFS和MLT生成的收集树分别由ISPA和IDGS链路调度算法进行调度。很显然,相比其他各种算法的任意组合,本文算法的数据收集时间更低。此外,当节点密度较高时,本文算法的优势更为明显。例如,当部署200个节点时,本文算法结果分别比MLTIDGS和MLTISPA高出13%和28%。这表明本文收集树构建和链路调度策略在降低数据收集延时方面的性能更低,同时可以保证较高的可靠性。请注意,数据收集树相同时,IDGS考虑了链路的流量负载,因此IDGS在数据收集时需要的时隙数量低于ISPA。另一方面,由于不同的链路调度算法得出不同的链路调度结果,因此难以看出BFS或MLT在降低数据收集延时方面的性能是否更优。

现在研究SINR阈值约束不同时,本文算法需要多少时隙。节点数量固定为100,而最小SINR阈值范围为0～30 dB,步进量为5 dB。图1(b)给出了LLHC-MWF和其他各种算法组合的仿真结果。

图1 数据收集所需时隙数量

很显然,当最小SINR阈值上升时,所有算法的数据收集时间均会上升,原因是当链路对干扰的敏感性增加时,每个时隙内的链路调度数量下降。然而,在不同的最小SINR阈值条件下,本文算法的性能始终优于其他算法。此外,当最小SINR阈值相对严格时,本文算法的优势更为明显。尤其地,当SINR的阈值为20 dB时,本文算法所需时隙量分别比MLT-IDGS和BFSISPA算法少31个和46个时隙。另外观察到,当SINR阈值超过20 dB时, LLHC-MWF相对其他算法的性能优势有轻微下降。原因是当SINR阈值较大时,收集树上大量链路不兼容,因此即使它们相对其他没有入选收集树的链路受到的干扰较少,但是仍然无法在同一时隙内调度。

下面研究在不同算法生成的数据收集树上,节点需要转发的流量。仿真结果见图2(a),节点数量范围为50～200。可以发现,LLHC的平均转发流量低于BFS算法,但高于MLT算法。原因是LLHC与BFC算法不同,LLHC算法在构建收集树时考虑了子树的规模,因此流量负载在网络上分布的更均衡。当节点密度增大时,MLT算法的平均转发流量基本不变,原因是在树的每一层,该算法均努力实现链路最大流量负载最小化。然而,如图1所示,该算法完成一轮数据收集所需时间要长于LLHC算法。这表明在转发负载和数据收集延时之间需要进行折衷。

本文还研究了数据收集期间,每个节点的最大队列长度,以确定节点的最小缓存量。仿真结果见图2(b)。

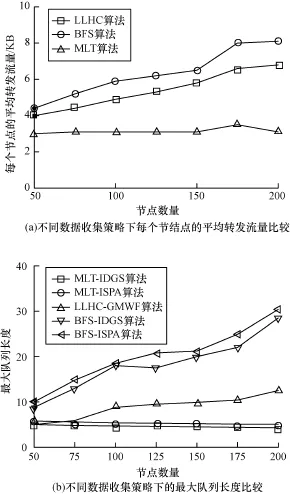
图2 节点的平均转发流量和最大队列长度对比

很显然,LLHC和MWF算法的最大队列长度远小于基于BFS的数据收集策略。此外,当节点密度上升时,本文算法的最大队列长度缓慢上升。如果区域内有200个节点,则LLHC-MWF的最大队列长度为13,只是BFS策略的1/3。假设报文大小为1KB,则本文算法所需缓存量小于20 KB,基本在大多数在用传感器节点的承受范围内。基于MLT的数据收集策略的最大队列长度低于5,且与节点密度无关,具体原因与上文讨论的每个节点的平均转发流量类似。同时也可以发现,如果数据收集树相同,则IDGS需要的缓存量低于ISPA。这是因为IDGS在每个时隙内的平均链路调度量高于ISPA(图1)。

另外,本文还研究了Sink位置对数据收集延时的影响。共进行了2组实验:一组中的Sink随机部署;另一组位于区域中央。仿真结果见图3,图中CS和RS分别表示中央部署Sink和随机部署Sink。很显然,如果Sink随机部署,则各种数据收集策略需要的时间均会上升。原因是如果Sink在网络边缘区域,则只有少部分节点可以将数据直接传输给Sink,使之成为数据收集的瓶颈。然而,与其他算法相比,本文算法仍然明显降低了数据收集延时。

图3 Sink部署于区域中央和随机部署时的时隙数量

最后,考虑到在本文方案中,每个节点可以以较低频率广播固定功率的信标消息,其他节点通过测量信标消息的接收功率就可以确定以该节点为起点的链路的信道增益。然后,该信道增益信息将被发往Sink。最后,只需在Sink上周期性运行LLHC和MWF算法,并将获得的采集树、链路调度和功率分配输出给所有节点即可实现可靠的数据收集,避免了由于链路失效所导致的节点多次数据转发和冗余传输问题,从而节省了节点能量。总的来说,本文算法通过链路调度和功率分配的联合优化,在保证数据收集可靠性的前提下,可以实现整个网络的能量有效性,进而延长网络寿命。

6 结束语

本文研究了无线传感器网络中基于收集树的数据收集问题,通过构建合适的数据收集树、调度收集树上的链路、在每个时隙内为活跃链路分配功率,以较低的时延和较高的可靠性,实现传感器的数据收集任务。将该问题分为2个子问题,并为每个子问题提供一个启发式算法。仿真实验结果表明,该算法在不同的节点密度和最小SINR阈值条件下,不论Sink位于何处,均可以明显降低数据收集延时。同时,通过使用本文算法,流量负载在网络上的分布更为均匀,网络寿命也更长。本文下一步工作的重点是研究机会移动传感器网络中基于压缩感知的可靠数据收集方案。

[1] Daflapurkar M P M,Patil B P.Performance Evaluation of WSNParametersUsingReinforcementLearning:A Survey[J].Performance Evaluation,2013,1(9):1360-1365.

[2] Liu Xiang,Jun Luo,Rosenberg C.Compressed Data Aggregation:Energy-efficientandHigh-fidelityData Collection[J].IEEE/ACM Transactions on Networking, 2013,21(6):1722-1735.

[3] 张希伟,戴海鹏,徐力杰,等.无线传感器网络中移动协助的数据收集策略[J].软件学报,2013,24(2): 198-214.

[4] 胡升泽,包卫东,王 博,等.无线传感器网络基于多元簇首的分簇数据收集算法[J].电子与信息学报, 2014,36(2):403-408.

[5] 奎晓燕,杜华坤,梁俊斌.无线传感器网络中一种能量均衡的基于连通支配集的数据收集算法[J].电子学报,2013,41(8):1521-1528

[6] 杨 靖,徐 迈,赵 伟,等.传感器网络中一种能量高效的数据收集算法[J].系统工程与电子技术, 2011,33(3):650-653

[7] 谭金勇,杨中亮.基于多信道的快速数据收集MAC协议[J].计算机工程,2013,39(12):107-110.

[8] Andrews M,Dinitz M.Maximizing Capacity in Arbitrary Wireless Networks in the SINR Model:Complexity and Game Theory[C]//Proceedings of IEEE INFOCOM’09. [S.1.]:IEEE Press,2009:1332-1340.

[9] Behzad A,Rubin I.Optimum Integrated Link Scheduling and Power Control for Multihop Wireless Networks[J]. IEEE Transactions on Vehicular Technology,2011,56(1): 194-205.

[10] Incel O D,Ghosh A,Krishnamachari B,et al.Fast Data Collection in Tree-based Wireless Sensor Networks[J]. IEEE Transactions on Mobile Computing,2012,11(1): 86-99.

[11] Fu L,Liew S C,Huang J.Joint Power Control and Link SchedulinginWirelessNetworksforThroughput Optimization[C]//Proceedings of ICC’08.[S.1.]: IEEE Press,2008:3066-3072.

编辑 索书志

A Data Collection Algorithm Based on Reliability in Wireless Sensor Network

HUANG Yuan1,2
(1.School of Information Science and Technology,Northwest University,Xi’an 710127,China; (2.Department of Computer Application,Shaanxi Academy of Governance,Xi’an 710068,China)

To achieve low-latency,high-reliability data gathering in Wireless Sensor Network(WSN),this paper formulates the joint problem of tree construction,link scheduling and power assignment for data gathering into an optimization problem,with the objective of minimizing data gathering latency.It divides the problem into two sub problems:construction of a low-latency data gathering tree,jointly link scheduling and power assignment for the data gathering tree.This paper proposes a polynomial heuristic algorithm for each sub problem and conducts extensive simulations.Simulation results show that the proposed algorithm achieves much lower data gathering latency than existing data gathering strategies while guaranteeing high reliability.

Wireless Sensor Network(WSN);data collection;link scheduling;power assignment;SINR constraint; delay;reliability

黄 媛.无线传感器网络中一种基于可靠性的数据收集算法[J].计算机工程,2015,41(2):85-90,95.

英文引用格式:Huang Yuan.A Data Collection Algorithm Based on Reliability in Wireless Sensor Network[J]. Computer Engineering,2015,41(2):85-90,95.

1000-3428(2015)02-0085-06

:A

:TP393

10.3969/j.issn.1000-3428.2015.02.017

黄 媛(1979-),女,讲师、硕士,主研方向:无线传感器网络,信息处理。

2014-03-13

:2014-04-09E-mail:484895081@qq.com