数据隐私保护的社会化推荐协议

刘曙曙，刘安，赵雷，刘冠峰，李直旭，郑凯，周晓方

(1.苏州大学 计算机科学与技术学院，江苏 苏州 215000；2.江苏省软件新技术与产业化协同创新中心，江苏 南京 211102)

1 引言

推荐系统是一系列通过对用户或其购买行为进行分析，从而自动为用户推荐其可能感兴趣的信息和商品的算法集合。协同过滤算法出现以来就受到了广泛关注，但随之而来的“冷启动”问题却制约了该算法的进一步使用。为解决这一问题，研究学者们提出了基于邻域的社会化推荐方法[1,2]，该方法指出，将基于社交网络拓扑图得到的用户关系引入到推荐系统中，可以有效解决协同过滤计算过程中由于新用户缺少历史行为数据而带来的“冷启动”问题。基于邻域的社会化推荐算法得到普遍关注，同时，大量最新的研究也表明，该算法明显优于传统推荐算法。

尽管推荐系统能够帮助人们在海量数据中高效快速过滤掉大量无关信息，但是，这一过程带来的信息泄露却值得人们担忧。在传统的推荐系统中，用户的历史行为数据，如购物记录、对于电影或物品的评分记录等，都必须作为数据上传到推荐系统服务器。一旦这些信息发生泄漏，攻击者便可以基于以上信息，迅速推测出用户的年龄、性别、身体状况等个人隐私信息，由此而引发的一些问题可能会对用户的生命财产造成威胁。

为了防止传统推荐系统中由于用户历史行为数据泄露而带来的担忧，研究学者们提出了一系列解决方案。Canny[5]最初提出了针对推荐系统的隐私保护方案，通过借助同态加密和一个端对端的协议，他能够为多种基于协同过滤的推荐系统提供隐私服务。该方案同样在文献[4,6]中得到了应用。借助随机扰动技术，Polat和Du[7]将用户的历史行为数据进行一定程度的干扰后再将其发送给推荐服务提供商，从而保证了用户的数据隐私安全。文献[8]使用了相同的原理来实现这一目标，他们都能够保证用户的历史行为数据在推荐服务提供商端的安全。Jorgensen[3]等提出利用差分隐私技术可以保证目标用户无法从推荐结果中推测任何和其他用户相关的信息，从而保证了其他用户个人隐私的安全性。不同于上述传统推荐系统中的问题模型，在社会化推荐系统中，以推荐系统服务提供商及社交网络服务提供商为主要参与方。在现实生活中，推荐系统服务提供商通常对应在线电子商务平台，他们持有用户的历史行为数据，却没有完善的社交网络拓扑图；社交网络拓扑图通常来自于第三方的在线社交网络服务提供商，如FaceBook或者Twitter等，他们都拥有用户信赖及用户数据信息。但是，出于对社交网络拓扑图拥有重要的利益价值和维护用户隐私的考虑，在线社交网络服务提供商并不愿意将数据信息提供给推荐系统服务提供商。同样，推荐系统服务提供商愿意为用户提供高效的推荐服务，但是并不愿意透漏用户的历史行为数据。

出于对以上实际情况的考虑，本文认为在社会化推荐系统中，保证两主要参与方的数据隐私安全是完成社会化推荐的前提。上述方案虽然能够有效解决传统推荐系统中用户隐私保护问题，但是这些方案并不适用于本文的问题模型。如何能够在保护双方数据隐私的前提下，实现两参与方协同计算的问题是本文的重点，将在后面详细讲解。

2 相关背景及问题定义

在基于邻域的社会化推荐系统中，通常有2个参与方，分别称为Alice和Bob。Alice代表持有用户历史行为数据的推荐系统服务提供商（如ebay、淘宝等电子商务平台），Bob是拥有社交网络拓扑图的第三方社交网站（如Facebook、Twitter等）。本文分别对以上2个数据模型给出形式化的定义。

定义1用户历史行为二分图。如图1（a）所示，用户历史行为数据图Gt=(U,I,Et)是一个单向二分图，其中，U(∣U∣=M)是所有用户的集合，I(∣I∣=N)是物品集合，Et是由用户U指向物品I的单向边集合，每一条边都附有权重值w(u,i)≥0，w(u,i)＞0时，表示用户u对于物品i的相应评分或购买频次，当用户u未曾购买过物品i,w(u,i)=0。

定义2用户社交网络拓扑图。如图1（b）所示，社交网络拓扑图Gs=(U,Es)是一个由用户集合U和用户关系边Es构成的无向图，其中，Es(u,v)表示用户u和v之间存在联系。

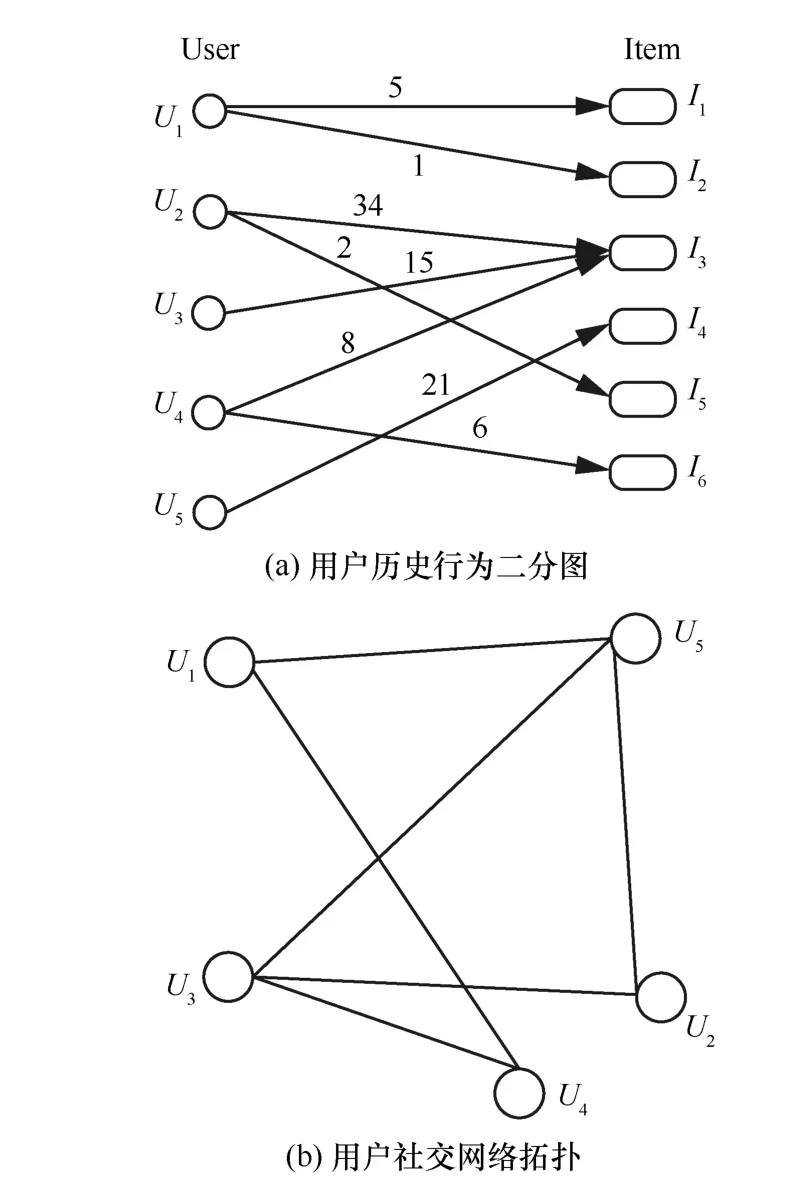
图1 用户历史行为二分图和用户社交网络拓扑

上述假设模型可以方便地扩展到其他应用领域，如在Last.fm中，边Et(u,i)表示用户u听过作者i的歌曲，在Brightkite.com中，边Et(u,i)表示用户u曾经访问过位置i，在上述假设中，权重值w(u，i)分别代表了用户u听过作者i的歌曲的次数，以及用户u曾经访问过位置i的次数。同样，各种类型的在线社交网站均可映射到定义2的模型中，如关系边（u,v）既可表示Facebook中用户u和v之间的好友关系，也可以代表Twitter中用户之间的“Following”关系。

定义3基于邻域的社会化推荐。假设两参与方Alice和Bob，Alice拥有用户历史行为数据，Bob拥有社交网络拓扑图（以及用户之间相似度度量算法sim），Alice和Bob通过合作计算，为目标用户u∈U，推荐K个评分最高的物品Ru∈I。

对于Alice中的任一目标用户u，Alice将会为u推荐K个得分最高的物品，记为集合Ru。其中，s(u,i)，即对于用户u而言物品i的得分

其中，sim(u,v)是用户u和v之间的相似度值，在非社会化推荐系统中，如图2(a)所示，sim(u,v)的计算主要基于用户的历史交易记录向量，常用方法有皮尔逊相关系数法、余弦相似度以及基于概率的相似度计算方法等，其中前2种方法使用最为广泛。在社会化推荐系统中，如图2(b)所示，相似度的计算通常基于社交网络拓扑图（即图中用户之间的邻接矩阵），常用方法有共同邻居（common neighbor），Katz以及随机游走（random walk with restart）等。w(v,i)是用户v与物品i的连接边的权重值。

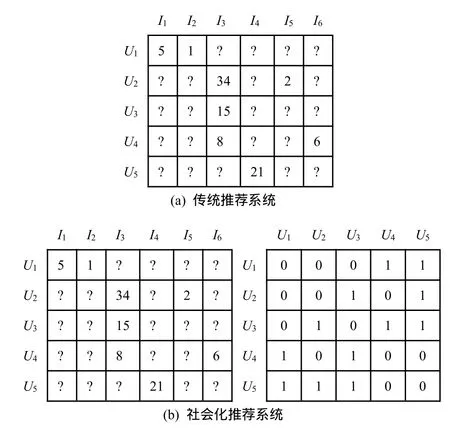
图2 传统和社会化推荐系统

在社会化推荐中，sim(u,v)的计算依赖于社交网络拓扑图Gs。为了能够完成社会化推荐，Alice即电子商务平台必须利用社交网络拓扑。出于商业利益或维护用户隐私的权益，Bob即社交网络拓扑图的持有者，并不愿意将私有数据，社交网络拓扑图直接提供给Alice使用，保证两参与方的数据隐私安全是完成社会化推荐的前提。下面将给出保护隐私的社会化推荐的定义。

定义4保护隐私的社会化推荐。假设两参与方Alice和Bob，Alice拥有用户历史行为数据，Bob拥有社交网络拓扑图以及用户之间相似度度量算法sim，Alice和Bob通过合作计算，为目标用户u∈U，推荐K个评分最高的物品Ru∈I，计算过程中，双方私有信息（如Gt和Gs）不能暴露给对方。

假设前提：定义中的推荐结果都是基于某一时刻的静态图谱Gt和Gs展开的。对于图谱Gt和Gs的动态更新，需要重新运行协议，更新推荐结果。下面将给出该问题的具体解决方案。

3 保护隐私的社会化推荐系统

针对社会化推荐系统需要在两方隐私数据上进行协同计算，本文提出了2种数据隐私保护的社会化推荐协议，可以同时保护推荐系统服务提供商和社交网络服务提供商的数据隐私。其中，基于不经意传输的社会化推荐，计算代价较小，适用于对推荐效率要求较高的应用。基于同态加密的社会化推荐，安全程度较高，适用于对数据隐私要求较高的应用。下面是2个协议的详细介绍。

3.1 基于不经意传输的社会化推荐

不经意传输(OT，oblivious transfer)是安全计算领域的重要工具，在众多问题中得到了广泛应用。借助不经意传输协议，可以高效地实现两方安全乘法计算[13]。计算过程中，两参与方私有数据信息安全完成后，结果由两方以和形式秘密共享，即参与方A持有数据a，参与方B持有数据b，利用不经意传输乘法协议后，A将持有结果x，B持有结果y，并且满足公式x+y=ab。相关细节参见文献[13]。

根据定义4，Alice持有数据Gt，Bob持有数据Gs。对于目标用户u，Bob可以根据事先确定好的相似度计算方法计算出sim(u,v)(v是除u外的所有其他用户)。以物品i为例，Bob端持有相似度向量SIM={sim(u,u1),sim(u,u2),…,sim(u,um)}，Alice持有物品i的评分向量Wi={w(u1,i),w(u2,i),…,w(um,i)}，根据式（1）可知，对于目标用户u而言，物品i的推荐得分s(u,i)为对应位积之和。具体算法如下。

算法1基于OT乘法的推荐得分算法

输入：Alice端Gt=(U,I,Et)

在计算过程中，使用OT乘法直接算出所有用户和物品之间的乘积，其复杂度为MN。但是由于用户历史行为记录是一个及其稀疏的矩阵，通常为M+N，直接对所有元素进行OT乘法操作，会产生大量不必要的计算。通用的解决方案是，Alice将用户历史行为记录矩阵的数据分布情况（0为用户未曾够买过物品；1为用户购买过物品）共享给Bob，同样Bob也需要将自己数据分布情况共享给Alice，两端仅需计算sim(u,uj)≠0和w(uj,i)≠0的项，从而减少不必要的计算开销。在这一共享过程中，两方共享的仅为数据分布情况，并未涉及两方的数据值信息，在对安全要求不是很高的情况下，该方法是安全可信的。

利用OT乘法协议完成物品的推荐得分计算后，所有物品的推荐得分由Alice和Bob以加法和形式秘密共享，即Alice端持有s1，Bob持有s2，同时s1+s2=s。

接下来，需要从所有候选物品中，挑选出K个推荐得分最高的物品推荐给用户。因为最终只需要将K个推荐得分最高的物品推荐给目标用户即可，K个物品之间的排列顺序并不影响推荐，所以采用线性时间复杂度的随机选择算法[14]来实现TopK选择。

随机选择算法的基本思想是：随机选择枢纽元，将数据分为2个独立的部分，其中一部分的所有数据都比枢纽元小，另外一部分的数据都比枢纽元大，然后再按此方法继续对其中某一部分数据进行划分，直到找到的枢纽元在整个序列中处于K的位置。具体算法如下。

算法2安全的TopK选择算法

输入：推荐得分向量S={s1,s2,…,sn}

输出：K个最高推荐得分物品集合Ru

Yao协议[9,10]允许2个半诚实参与方分别输入x和y作为一个任意函数f(x,y)的输入，协议能够保证两参与方私有信息安全的前提下，准确计算函数值，没有任何关于输入或者中间值的相关信息泄露。关于Yao协议的定理证明可以参见文献[10]。基于Yao协议实现的两方安全计算框架FGC[11]近年来凭借其高效的性能得到普遍使用。本文将基于FGC中的2-ADD和2-CMP这2个基本模块，实现TopK选择的比较模块。其中，2-ADD可以实现任意2个L位整数之间的加法，2-CMP可以实现任意2个L位整数之间的比较，输出结果为0或1。2-ADD可以以密文形式还原推荐得分，随后使用2-CMP完成得分的比较即可。

3.2 基于同态加密的社会化推荐

在上述协议中，为了减少不必要的开销，实现高效率计算，Alice和Bob需要将本身的数据分布情况共享给对方，尽管这一共享并没有泄露两参与方实际的数据值信息，但对于高安全级别的系统而言仍然存在一定程度的安全隐患。为了实现更高层次的安全保护，防止任何形式的信息泄露，提出了基于同态加密的完全隐私保护的社会化推荐协议。

Paillier同态加密系统[8]是Paillier于1999年发明的用于公钥加密的概率非对称算法。在本文中，用E(x)表示对明文x的Paillier加密函数，D(x)表示对密文x的Paillier解密函数，证明参见文献[8]。该加密系统具有加法同态性质，即2个密文乘积的解密值，与两密文对应明文的和相等；密文的k次幂解密值，与k和对应明文的乘积相等；Paillier加密系统的语义安全特性保证了攻击者无法由给定密文导出任何相关明文信息。基于同态加密的推荐得分算法如下。

算法3基于Paillier同态机密的推荐得分算法

为了保证数据信息的安全，Bob端的相似度值需要用Paillier加密函数En加密后方可发送给Alice端，Paillier的语义安全特性保证了Alice无法从密文获取与Bob相关的任何信息。同时，鉴于Paillier加密的同态性质，Alice端可以单独计算出所有物品的推荐结果得分，得分以密文形式存在。Alice端推荐得分计算公式如下

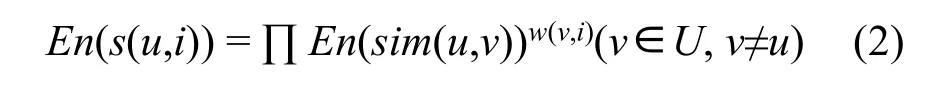
由于w(v,i)是Alice端的数据，所以Alice可以自动过滤掉w(uj,i)≠0的项，减少不必要的计算开销。基于Paillier完成推荐得分计算后，结果以密文形式由Alice持有，密钥由Bob端持有。

因为Pailler并不支持基于密文的比较操作，Alice无法单独实现安全的TopK选择。加法秘密共享能够保证推荐得分对于两参与方的保密，同时，加法和秘密共享形式能保证安全的TopK选择顺利进行。为了实现推荐得分的秘密共享，首先，Alice生成N个足够大的随机数r，并结合Paillier加密算法计算En(s-r)，密文结果发送给Bob；Bob借助其本身持有的密钥可以解密数据，从而得到s'=s-r。至此，Alice端持有随机数r，Bob持有s'，同时r+(s')=s。尽管Alice持有随机数r和推荐得分的密文，但是Alice并没有密钥，所以无法得知任何与中间结果s相关的任何信息。Bob持有密钥和s'，但是s'=s-r，由于随机数的干扰，Bob端无法推测出s的相关信息。

接下来，调用算法2提出的安全TopK选择算法，即可从所有候选物品中，挑选出K个推荐得分最高的物品推荐给用户。

4 理论分析

攻击模型：本文假设Alice和Bob都是半诚实的，两方将严格的执行协议，但是计算过程中两方也会尽可能地根据中间信息推测出更多的额外信息。针对恶意攻击模型的安全协议虽然存在，但是计算代价过大，在实际中并不实用。而针对半诚实模型的安全协议不但能够实现高效的计算，而且对恶意攻击模型下的安全协议研究具有重要参考价值。

4.1 安全性分析

如上所述，社会化推荐方法包括物品的推荐得分计算和TopK选择2个过程。此处将就这2个过程逐一分析。

本文就不经意传输和同态加密提出了2种不同的隐私保护方法来计算推荐得分，在不经传输乘法协议中，两参与方私有数据信息安全，计算完成后，结果由两方以和形式秘密共享，即参与方A持有数据a，参与方B持有数据b，利用不经意传输乘法协议后，A将持有结果x，B持有结果y，并且满足x+y=ab（相关安全性证明参见文献[13]）。在不经意传输乘法协议可信的前提下，基于不经意传输的推荐得分计算不会泄露任何一方的私有信息。

在基于同态加密实现的推荐得分计算中，为了保证数据信息的安全，Bob端将相似度值加密后发送给Alice端，Paillier的语义安全特性保证了Alice无法从密文获取与Bob相关的任何信息。同时，基于密文，Alice端可以单独计算出所有物品的推荐结果得分，得分以密文形式存在。为了实现加法秘密共享从而保证Garbled Circuit的调用，首先，Alice生成N个足够大的随机数r，并结合Paillier加密算法计算En(s-r)，密文结果发送给Bob；Bob借助其本身持有的密钥可以解密数据，从而得到s'=s-r。至此，Alice端持有随机数r，Bob持有s'，同时r+(s')=s。在此过程中，尽管Alice持有随机数r和推荐得分的密文，但是Alice并没有密钥，所以无法得知任何与中间结果s相关的任何信息。Bob持有密钥和s'，但是s'=s-r，由于随机数的干扰，Bob端无法推测出s的相关信息。

完成推荐得分计算后，所有得分由Alice和Bob以加法和形式秘密共享，即Alice端持有s1，Bob持有s2，同时s1+s2=s。结合这一特点，可以基于Garbled Circuit提供的2-ADD和2-CMP这2个基本模块完成TopK推荐。文献[10]指出在半诚实模型下，Garbled Circuit允许2个参与方分别输入x和y作为一个任意函数f(x,y)的输入，协议能够保证两参与方私有信息安全的前提下，准确计算函数值，没有任何关于输入或者中间值的相关信息泄露。这一性质保证了在TopK推荐过程中，任何与两方相关的输入或者中间信息都不会泄露，该TopK选择过程安全可靠。

综上，基于不经意传输的社会化推荐方法和基于同态加密的社会化推荐方法，都能在保证两方（推荐系统服务提供商和社交网络服务提供商）数据隐私的前提下，为目标用户提供精确的推荐。

4.2 复杂度分析

如表1所示为两方案的复杂度分析，其中，|U|表示用户个数，|I|表示物品个数，|Et|表示用户历史购买记录条数，t为推荐得分的二进制比特数。在基于不经意传输的社会化推荐中，步骤1对应OT乘法协议计算推荐得分，步骤2是安全的TopK选择。在基于同态加密的社会化推荐方法中，步骤1至步骤3分别对应了基于Paillier同态加密的推荐得分，加法秘密共享及安全的TopK选择。

表1 复杂度分析

通过算法1，可以明显看出，在不经意传输协议的步骤1中，双方共需调用不经意传输乘法协议|Et|次。同时，由上文可知，在TopK选择中基本单元包含2个2-ADD和1个2-CMP模块，对于t位的电路输入，共包含非异或门3t+1个。因为采用了线性时间复杂度的随机选择算法[14]来实现TopK选择，其平均比较次数为|I|，所以共需非异或门(3t+1)|I|个。

在基于同态加密的社会化推荐方法中，由算法3可知，为了计算物品得分，Bob共需|U|次加密操作，Alice共需|I|次指数操作。在步骤2，即加法秘密共享中，Alice共需|I|次加密和指数操作，Bob需要|I|次解密操作。由于两方案使用同一TopK协议，所以复杂度仍为(3t+1)|I|。下面将通过实验对两方案的性能做进一步的比较。

5 实验部分

本文提出了2种方案，都能够在保证两参与方私有信息（Gt和Gs）不泄露的前提下，为目标用户提供精确的推荐。在这一部分，将使用4个公开数据集测试所提的方法，数据集相关统计信息如表2所示。

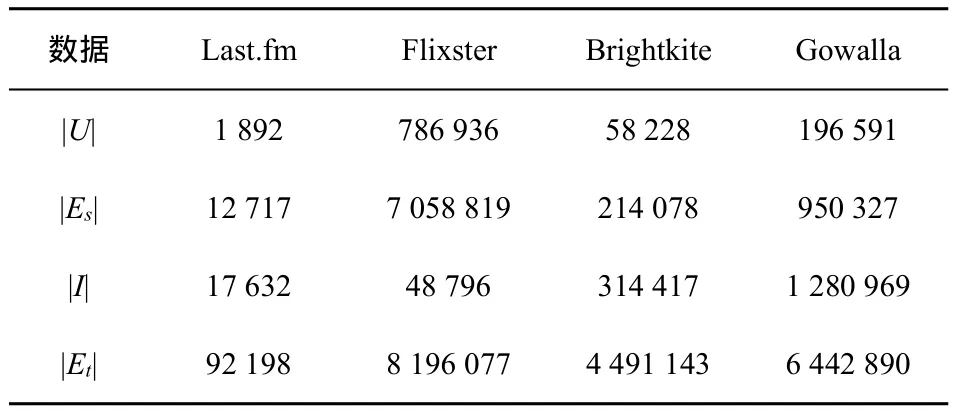
表2 数据集统计信息

其中，|U|表示用户个数，|I|表示物品个数，|Es|是用户之间的关联边数，|Et|表示用户历史购买记录条数，从表中数据可以看出，用户历史记录矩阵相当稀疏。本实验主要包含了4个数据集，Last.fm[1]是一个相对较小的数据集，主要包含了不同用户对音乐家的收听习惯。Flixter.com[2]是一个电影评分网站。Brightkite.com[3]和Gowalla.com[4]则是基于位置信息的信息分享网站，主要记录不同用户在不同地点有多次的登录行为。

实验在2.6 GHz CPU，1TB RAM的服务器上执行，软件环境为Centos Linux release 7.1，JDK7。

使用Java实现了Paillier同态加密系统，实验中，密钥空间设为1 024 bit（1 024 bit相当于对称密钥方案中80 bit的安全级别，在这个设置下，可以忽略由于密码被攻破而带来的信息泄露）。基于FGC框架，实现了安全的TopK选择协议。默认情况下，推荐数K设置为10。

实验结果如表3和表4所示，表3和表4分别是方法1和方法2对应的时间统计。表3中，步骤1对应OT乘法协议计算推荐得分，步骤2是安全的TopK选择。表4中包含了3步操作，基于Paillier同态加密的推荐得分以及得分的秘密共享及安全的TopK选择。

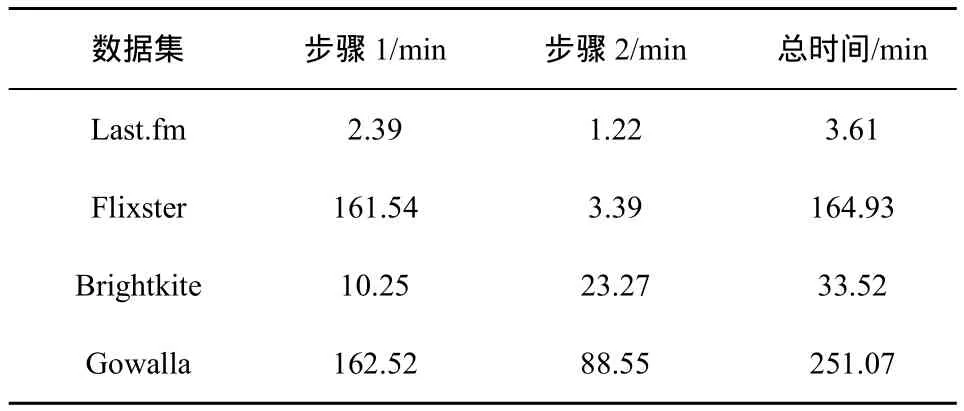
表3 基于OT乘法的社会化推荐系统时间统计

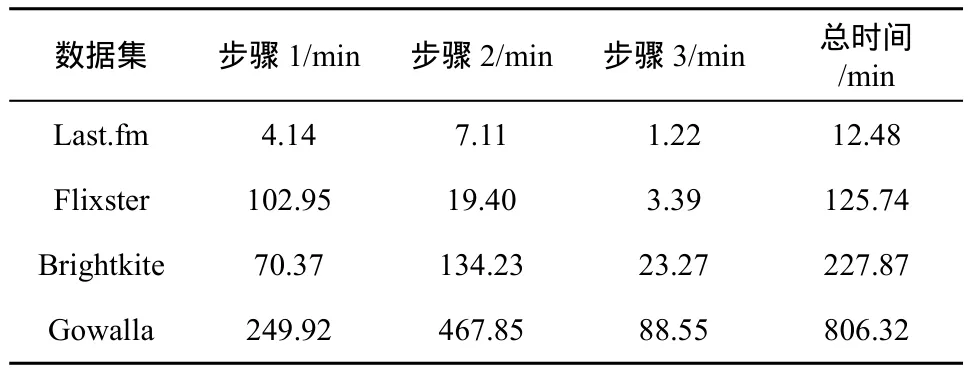
表4 基于同态加密的社会化推荐系统时间统计

结合算法分析可知，由于矩阵的稀疏度影响，表3中步骤1的时间主要与非零项相关。步骤2中时间和物品数|I|成正比。由于表4中步骤1推荐得分计算与|Et|成正比，步骤2加法秘密共享与|I|成正比。

从表中可以看到，除了Flixster外的其他3个数据集上，基于OT乘法的社会化推荐协议比基于同态加密的社会化推荐方案更为高效。而Flixster由于矩阵的非零项记录|Et|远大于|I|，所以基于OT乘法的协议并没有因为省略加法秘密共享操作而获得足够优势。在方法选择过程中，用户可以根据自己的数据集特性及要求选择合适的方案。

6 结束语

本文提出了2种数据隐私保护的社会化推荐协议。两协议都能够在保证不泄露两参与方私有数据信息的前提下，完成社会化推荐。其中，基于不经意传输的社会化推荐，计算代价较小，适用于对推荐效率要求较高的应用。基于同态加密的社会化推荐，安全程度较高，适用于对数据隐私要求较高的应用。4组真实数据集实验表明，本文提出的方案切实可行，用户可以根据自身需求选择合适的方案。

[1]KONSTAS I,STATHOPOULOS V,JOSE J M.On social networks and collaborative recommendation[A].32nd International ACM SIGIR Conference on Research and Development in Information Retrieval[C].ACM,2009.195-202.

[2] YUAN Q,ZHAO S,CHEN L,et al.Augmenting collaborative recommender by fusing explicit social relationships[A].Workshop on Recommender Systems and the Social Web[C].2009.2009.

[3] JORGENSEN Z,YU T.A privacy-preservingframework for personalized,social recommendations[A].EDBT[C].2014.571-582.

[4] HAN S,NG W K,YU P S.Privacy-preserving singular value decomposition[A].ICDE[C].2009.

[5] CANNY J.Collaborative filtering with privacy[A].Security and Privacy,Proceedings of 2002 IEEE Symposium[C].IEEE,2002.45-57.

[6]MILLER B N,KONSTAN J A,RIEDL J.PocketLens:toward a personal recommender system[J].ACM Transactions on Information Systems(TOIS),2004,22(3):437-476.

[7] POLAT H,DU W.Privacy-preserving collaborative filtering[J].International Journal of Electronic Commerce,2005,9(4):9-35.

[8]BERKOVSKY S,EYTANI Y,KUFLIK T,et al.Enhancing privacy and preserving accuracy of a distributed collaborative filtering[A].2007 ACM Conference on Recommender Systems[C].ACM,2007.9-16.

[9] YAO A.How to generate and exchange secrets[A].Foundations of Computer Science 27thAnnual Symposium on[C].1986.162-167.

[10]LINDELL Y,PINKAS B.A proof of security of Yao's protocol for two-partycomputation[J].Journal of Cryptology,2009,22(2):161-188.

[11]HUANG Y,EVANS D,KATZ J,et al.Faster secure two-party computation using garbled circuits[A]. USENIX Security Symposium[C].2011,201(1).

[12]NAOR M,PINKAS B.Efficient oblivious transfer protocols[A].Proceedings of the Twelfth Annual ACM-SIAM Symposium on Discrete Algorithms, Society for Industrial and Applied Mathematics[C].2001.448-457.

[13]GILBOA N.Two party RSA key generation[A].Advances in Cryptology—CRYPTO'99[C].SpringerBerlin Heidelberg,1999.116-129.

[14]CORMEN T H.Introduction toAlgorithms[M].MIT Press,2009.