BOC(2n,n)信号码跟踪环多径误差分析

欧阳勖,孙希延,纪元法,施浒立

(1.桂林电子科技大学信息与通信学院,广西桂林 541004; 2.中国科学院国家天文台,北京 100012)

BOC(2n,n)信号码跟踪环多径误差分析

欧阳勖1,孙希延1,纪元法1,施浒立2

(1.桂林电子科技大学信息与通信学院,广西桂林 541004; 2.中国科学院国家天文台,北京 100012)

针对多径信号引起跟踪环多径误差的问题,基于经典接收机跟踪环结构,从鉴别函数分析着手,对BOC(2n,n)信号的码多径误差解析式进行推导,给出了多径误差与多径参数的变化关系,并分析了前置滤波带宽对BOC(2n,n)信号的多径误差包络的影响,Matlab仿真结果验证了理论推导的正确性,证明了窄相关技术能提供良好的码多径误差抑制性能,BOC信号码速率越高,抗多径性能越好,并且增加前置滤波带宽能有效改善信号抗多径性能。

多径误差;跟踪环;BOC(2n,n);多径包络

二进制偏移载波(BOC)调制具有特殊的谱分裂特性,能够在相同的导航频段提供更多的服务[1],经过BOC调制的信号具有比BPSK信号更尖锐的自相关函数,大幅度提高了定位精度和抗多径性能。因此,GNSS系统均采用BOC调制方式作为其主要调制方式。

多径误差是影响导航定位精度的主要误差源[2-4]。由于不具备时间和空间相关性,多径误差难以利用传统差分技术消除,而严重时多径误差会导致信号失锁[5]。抑制多径的方法主要包括特殊的多径抑制天线、抑制载波多径的后处理技术和抑制码多径的载波平滑技术,然而常用的多径减弱方法是接收机内部的相关技术,如窄相关技术、HRC、Strobe相关器等[6-7]。

很多研究对抗多径算法进行了探讨,却较少对多径信号引起的跟踪环多径误差进行量化分析,探讨多径信号参数与多径误差的关系。为此,在窄相关技术的基础上,推导了BOC(2n,n)信号的码跟踪多径误差的解析表达式,分析了码跟踪多径误差与多径信号各参数之间的关系,为进一步研究多径误差抑制算法提供理论支撑。

1 多径信号模型

多径信号滞后直达信号到达天线,多径信号的特征一般使用衰减系数、传播时延和载波相位变化来表示[2]。因此,接收机收到的信号是多径信号与直达信号的叠加信号:

其中:i=0为直达信号,i=1,2,…,M为多径信号;λ为信号幅度;αi为衰减系数;d(t)为导航电文;c(t)为伪随机码;cs(t)为副载波;τi为时延;ω0为中频频率;φi(t)为信号的相位。

为了简化分析,设λ=1,且忽略导航电文,省略相位的时间变量,则式(1)可简写为:

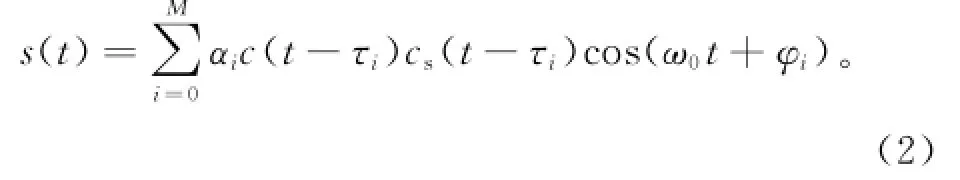
在经典接收机跟踪环中同相和正交支路各有3个相关器:对准、超前和滞后。假设载波环能准确地跟踪接收信号的频率,则同相和正交对准支路的本地码分别为:

经过计算,得到同相和正交支路的对准、超前、滞后相关值分别为:

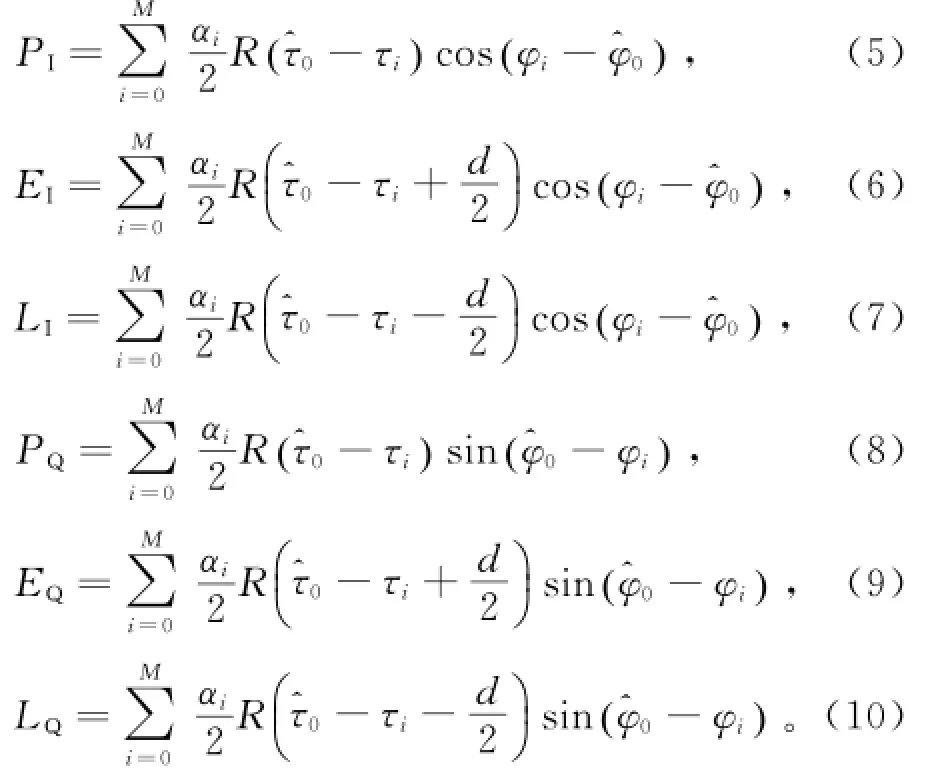
i=0

其中:^τ0为直达信号的时延估计;^φ0为直达信号的载波相位估计;R(τ)为BOC(2n,n)信号的自相关函数;d为超前和滞后支路的相关器间隔。

2 多径信号引起的码跟踪多径误差

2.1 BOC(2n,n)信号码跟踪多径误差分析

多径信号导致码鉴相曲线的零点发生偏移,产生伪码跟踪误差[3]。不失一般性,从码相鉴别曲线出发,以超前减滞后(EML)鉴相器为例,对码跟踪多径误差的解析式进行推导。设只有一条多径信号,对于连续的跟踪处理,设φe=0,即载波跟踪无误差,得到鉴相器输出为:

其中:τ=τ1―τ0为多径信号与直达信号相对时延;φ =φ1―φ0为相对相位,τe=^τ0―τ0为多径引起的码相时延误差;φe=^φ0―φ0为载波相位误差。式(11)可转化为:

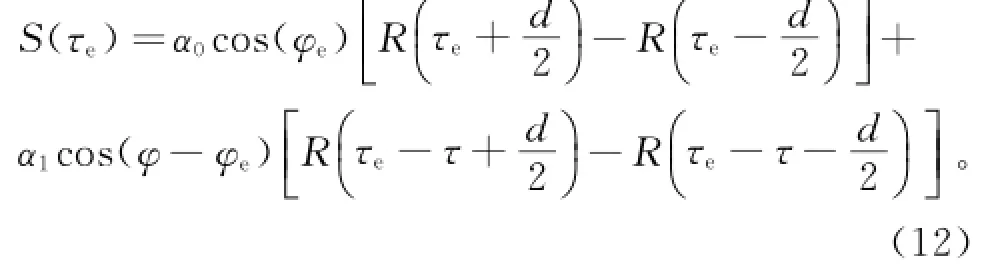
若到达接收机天线的只有直达信号,则EML鉴相器输出为:

其中:

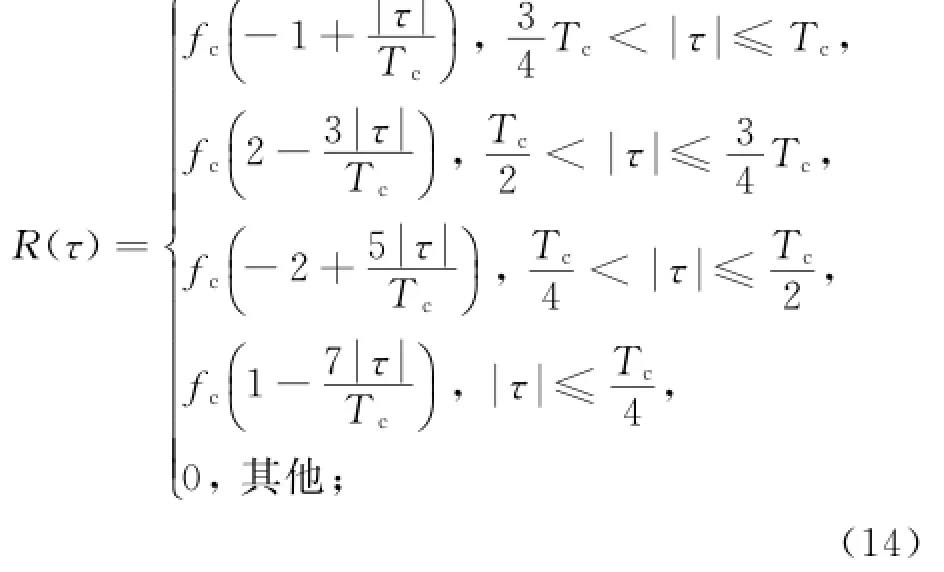
fc为伪随机码的码速率;Tc为伪随机码的码元宽度。BOC(2n,n)信号自相关函数的主峰宽度为0.5码片[8-11],因此,在后面的推导过程中d的最大值为0.25Tc。

若到达接收机天线只有一条多径信号,则EML鉴相器输出为:

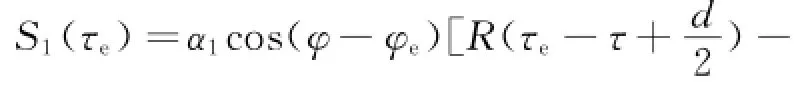
设φe=0,即载波跟踪无误差,根据式(12)～(14),得

其中:

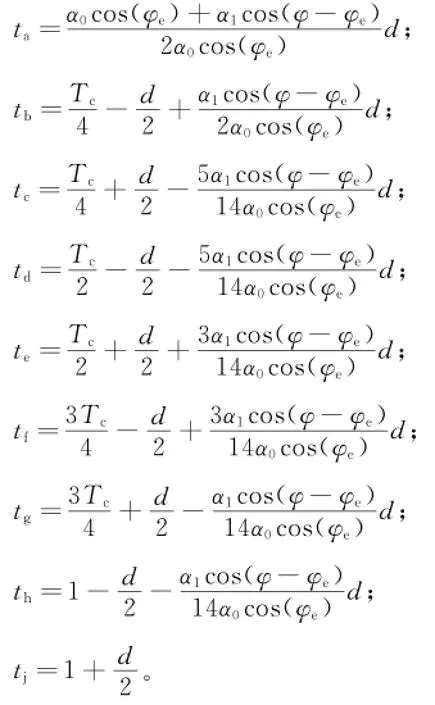
2.2 BOC(2n,n)信号抗多径性能评估

评估信号抗多径性能一般采用多径误差包络和平均多径误差曲线2个准则。默认接收机前置滤波带宽为无限带宽,假设前置滤波带宽有限,对BOC (2n,n)信号抗码相跟踪多径误差性能进行评估。设前置滤波带宽为βr,自相关函数与功率谱密度的关系为[9]:

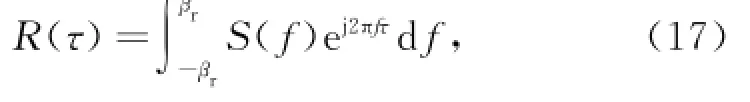
其中,S(f)为功率谱,则码跟踪多径误差包络为:

平均多径误差为:其中:α为多径与直达信号幅值比;d为超前减滞后相关间隔。

3 仿真结果

令φe=0,直达信号与多径信号相对幅度比α= α1/α0,从式(16)可看出,多径误差与相对时延τ、超前与滞后相关间隔d、相对相位φ和相对幅度α密切相关。

当α=0.5,不同超前减滞后相关间隔码跟踪误差与多径时延的关系如图1所示。从图1可看出,相关间隔越窄,码跟踪误差越小,抗多径性能越强。当多径时延τ≥1.05Tc时,多径信号与直达信号的相关性消失,不存在多径误差,因此,窄相关技术具有良好的抗多径性能。

图1 码跟踪误差与多径时延的关系Fig.1 The relationship between code tracking error and multipath delay

当d=0.25Tc,φ=0时,码跟踪误差与信号幅度比的关系如图2所示。从图2可看出,信号幅度比的增加造成码跟踪误差增大,且误差增加程度随信号幅度比的增加呈现不同变化趋势。

图2 码跟踪误差与信号幅度比的关系Fig.2 The relationship between code tracking error and signal amplitude ratio

当α=0.5,d=0.25Tc,码跟踪误差与多径相位的关系如图3所示。从图3可看出,码跟踪误差随多径相位呈周期性变化。当多径相位为0.5π、1.5π时,多径信号与直达信号正交,不存在码跟踪误差,且误差大小由多径相位与相对时延共同决定。

图3 码跟踪误差与多径相位的关系Fig.3 The relationship between code tracking error and multipath phase

当d=0.1Tc,rMD=―6 dB,βr=24 M Hz,BOC (2,1)、BOC(4,2)、BOC(8,4)和BOC(10,5)四种BOC(2n,n)信号的多径误差包络与平均多径误差如图4所示。从图4可看出,不同参数的BOC(2n,n)信号具有形状相似的码跟踪多径误差包络和平均多径误差曲线,而码速率高的信号比速率低的信号具有更好的抗多径性能。BOC(10,5)的码跟踪多径误差大小和范围最小,相对时延为1.1Tc时,码跟踪多径误差为0,且多径引起的最大误差小于2 m。BOC (2n,n)信号的抗多径性能随着码速率的增加而增强。对于平均多径误差曲线,BOC(2n,n)信号呈相似的变化。多径时延较短时,多径误差急速增加,当达到某一特定值后,随多径时延的增大,码跟踪多径误差缓慢降低至0.2 m。

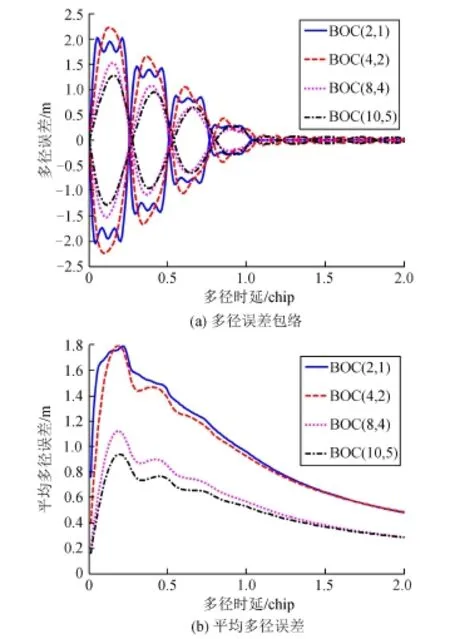
图4 rMD=―6 dB,βr=24 MHz时多径误差包络与平均多径误差Fig.4 Multipath error envelope and average multipatherror with rMD=―6 dB,βr=24 M Hz

当多径信号与直达信号幅值比rMD=―6 dB,前置滤波带宽βr=32 MHz时,多径误差包络及平均多径误差如图5所示。比较图4、5可知,当多径信号与直达信号幅值比不变,超前减滞后相关间隔一定时,增加前置滤波带宽可有效抑制多径误差,但过大的前置滤波带宽会引入更多噪声,造成信号能量损耗。

4 结束语

通过对码跟踪环的多径误差进行量化分析,运用Matlab软件验证了理论推导的正确性,得出了码跟踪多径误差与多径参数的关系。理论研究和仿真结果表明,BOC(2n,n)信号具有良好的抗多径性能,较窄的超前减滞后相关间隔能够抑制多径误差,且码速率越大,信号抑制多径误差能力越强,但窄相关技术并不能完全消除多径误差。此外,增加前置滤波带宽有利于抑制多径误差,但过大的前置滤波带宽会引入更多噪声,影响接收性能。

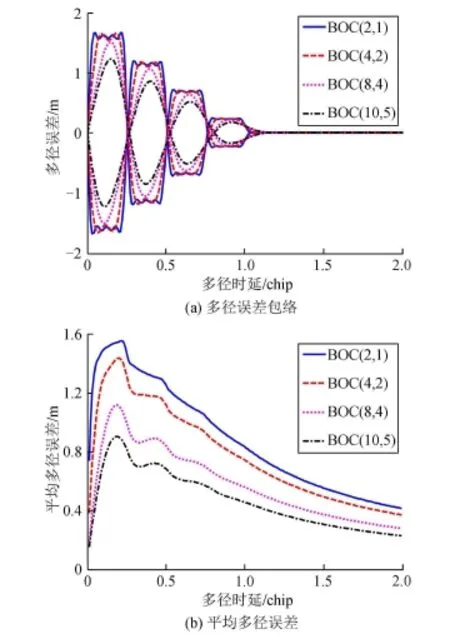
图5 rMD=―6 dB,βr=32 MHz时多径误差包络与平均多径误差Fig.5 Multipath error envelope and average multipath error with rMD=―6 dB,βr=32 M Hz

[1] Betz J W.Binary off set carrier modulations for radio navigation[J].Journal of the Institute of Navigation, 2001,48(4):227-246.

[2] 夏林元.GPS观测值中的多路径效应理论研究及数值结果[D].武汉:武汉大学,2001:49.

[3] Kaplan E D,Hegarty C J.GPS原理与应用[M].2版.寇艳红,译.北京:电子工业出版社,2007:89.

[4] 王尔申,张淑芬,张芝贤.GPS接收机抗多径技术研究现状与趋势[J].电讯技术,2011,51(1):114-119.

[5] Irsigler M,Eissfeller B.Comparison of multipath mitigation techniques with consideration of future signal structures[C]//Proceedings of the 16th International Technical Meeting of the Satellite Division of the Institute of Navigation,2003:2584-2592.

[6] Ray J K,Cannon M E.GPS code and carrier multipath mitigation using a multi-antenna system[J].IEEE Transactions on Aerospace and Electronic System, 2001,37(1):183-186.

[7] Van Dierendonck A J,Fenton P,Ford T.Theory and performance of narrow correlator spacing in a GPS receiver[J].Journal of the Institute of Navigation,1992, 19(3):265-283.

[8] 杨铁军,黄顺吉.GPS接收机跟踪环的多径误差分析[J].系统工程与电子技术,2002,24(9):13-15.

[9] Irsigler M,Hein G W,Eissfeller B.Multipath performance analysis for future GNSS signals[C]//Proceedings of the 2004 National Technical Meeting of the Institute of Navigation,2004:384-393.

[10] Hegarty C,Tran M,Betz J W.Multipath performance of the new GNSS signals[C]//Proceedings of the 2004 National Technical Meeting of the Institute of Navigation,2004:333-342.

[11] Simsky A,Sleewaegen J,Crisci M.Multipath and tracking performance of Galileo ranging signals transmitted by GIOVE-B[C]//Proceedings of ION GNSS conference,2008:213-222.

编辑:曹寿平

Multipath error analysis on the code tracking loop for BOC(2n,n)signals

Ouyang Xu1,Sun Xiyan1,Ji Yuanfa1,Shi Huli2

(1.School of Information and Communication Engineering,Guilin University of Electronic Technology,Guilin 541004,China; 2.National Astronomical Observatory,Chinese Academy of Sciences,Beijing 100012,China)

In view of the error aroused by the multipath signal in the code tracking loop,based on a classic receiver tracking loop structure,the code multipath expressions for BOC(2n,n)signals is deduced by analyzing the code discriminator function,the relation between the multipath error and multipath parameters is demonstrated,and the influence of different frontend bandwidth on the multipath envelop is studied.The correctness of the theoretical deduction is proved by Matlab simulation results,the narrow correlator can provide a favorable multipath mitigation performance and the mitigation performance becomes better when the code rate is increased.Additionally,the performance of multipath inhibition can be improved with larger front-end bandwidth.

multipath error;tracking loop;BOC(2n,n);multipath envelope

TN967.1

:A

:1673-808X(2015)04-0264-05

2015-03-11

国家自然科学基金(61162007,61271284,61362005);广西自然科学基金(2013GXNSFA019004);广西无线宽带通信与信号处理重点实验室主任基金(GXKL0614102,GXKL0614108);广西教育厅科研项目(YB2014143)

孙希延(1974―),女,山东安丘人,研究员,博士,研究方向为信号处理、卫星导航。E-mail:2246243917@qq.com

欧阳勖,孙希延,纪元法,等.BOC(2n,n)信号码跟踪环多径误差分析[J].桂林电子科技大学学报,2015,35(4):264-268.