TSC最佳投入策略的理论分析

陈 立*，申双葵，马庆安，解绍锋，郭 蕾

(1.国网四川省电力公司 成都供电公司，成都 610041;2.西南交通大学 电气工程学院，成都 610031)

晶闸管投切电容器(Thyristor Switched Capacitor，TSC)作为静止无功补偿器中的一员，具有投入速度快、损耗小、不产生谐波等优点［1］，可用于阻尼电力系统功率振荡［2］、提高电压稳定性［3］、动态性能［4］等作用。文献［5］基于人工神经网络(ANN)研究了稳态运行时TSC的控制策略;文献［6］研究了在电磁暂态仿真程序中TSC的建模问题;文献［7］给出了TSC工程设计需考虑的各个方面;文献［1，8］给出了TSC的投入控制策略:当电容器的初始电压与系统等效电压相等时，即晶闸管电压过零时触发，可使TSC投入时产生的谐波分量最小。但相关文献均未给出相应的理论证明。

从数学角度看，TSC投入后产生的谐波分量的频率均与TSC支路自然频率相同［1-2］，故可将谐波分量合并为一项，得到谐波分量的峰值;对谐波分量峰值求极小值点，得到TSC最小谐波分量投入的条件。本文将验证文献［1-2］的论述。

1 TSC投入最小谐波分量理论分析

为降低冲击电流，TSC中均串联一个电抗值很小的电抗器，如图1所示。设电源电压为:

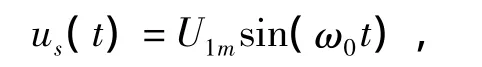
忽略支路电阻，TSC投入后其总电流表达式为［1-2］:

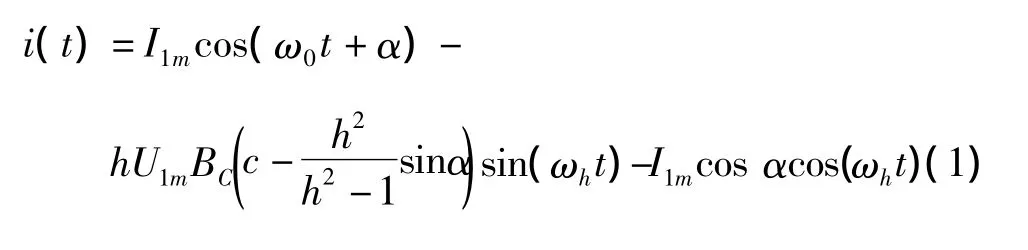
其中:U1m为TSC所在母线的基波电压幅值;ω0为系统额定基波角频率;BC为电容器基波电纳;α为TSC触发角;ωh=1 /为TSC支路的自然频率;h=ωh/ω0为自然频率与基波频率的比值;c=UC0/U1m;UC0为TSC中电容器初始电压;I1m=U1mBCh2/(h2-1)为TSC投入后的稳态基波电流分量。

可见，式(1)的第2、3项均为h次谐波分量。当考虑TSC的支路电阻时，这2项均随时间衰减至零。

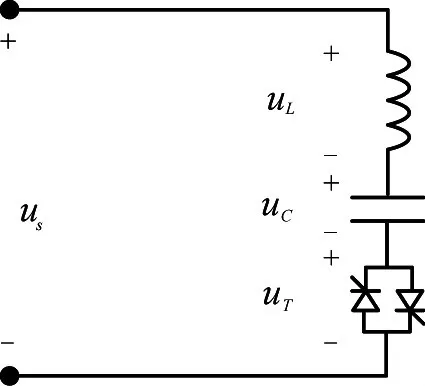
图1 具有串联电抗器的TSC

为方便，将式(1)中的谐波分量合并为:

由式(2)可知，为使谐波电流峰值最小，须使f(α，c)最小。考虑到 f(α，c)的极小值点满足df(ac)/dα=0。为此，对其求导得:

要使 df(a，c)/dα =0，须 cos α =0 或 sin α =c，即两者均可能为f(α，c)的极小值点。为找出极小值点，对式(3)再次求导，得:

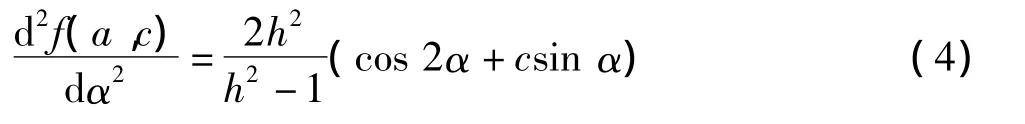
下面对可能的极小值点展开讨论。因正负半周的分析相同，这里仅讨论正半周的情况。

1)cos α=0

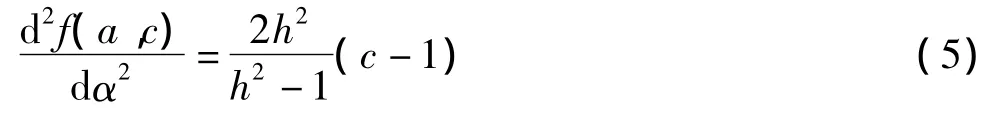
当 cos α =0 时 sin α =1，代入式(4)得:当 c=1 时，d2f(a，c)/dα2=0;c＜1 时 d2f(a，c)/dα2＜0，即 cos α =0 为极大值点;当 c＞1 时，cos α =0为极小值点。

2)sin α=c

当 sin α =c时 sin2α =c2，cos 2α =1-2c2，代入式(4)得:

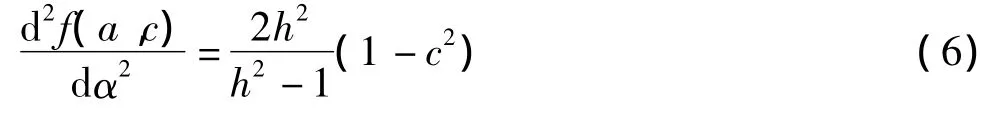
当 c=1 时，d2f(a，c)/dα2=0;当 c＜1 时，d2f(a，c)/dα2＞0，即 sin α =c为极小值点;当 c＞1时，d2f(a，c)/dα2＜0，即 sin α =c为极大值点。

当0＜c＜1时，若 α∈［0，π/2］且满足 sin α =c，则sin(π-α)=c。由式(1)可见，触发角 α为与π-α具有相同的h次谐波分量峰值，两者均可选择。因此，对于给定电容器初始电压，TSC可被触发2次。关于这一点，在文献［1-2］均未给出说明。

由以上讨论可知，当c＜1时sin α=c为极小值点;当c＞1时，cos α=0为极小值点。

综合负半周的情况，当│c│＜1时，触发角应选为使sin α=c;否则，应选择在电压峰值触发。触发角与电压初值的关系如图2所示。

该结论与文献［1-2］相同，从理论上证明了其论述的合理性。

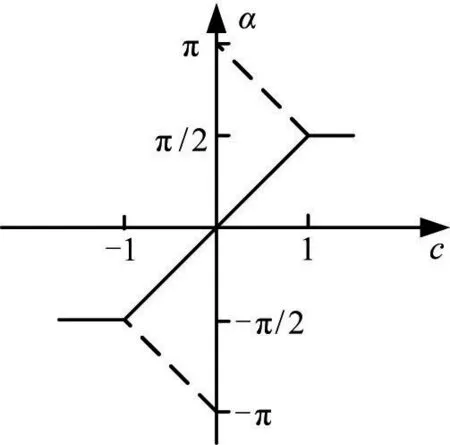
图2 TSC触发角与初始电压的关系

2 谐波电流峰值的分布规律

当│c│＜1 时，触发角应选为 sin α =c，由式(2)可求出:

由式(1)、式(2)可得h次谐波电流分量、基波电流分量峰值之比:

实际工程中h＞3，典型情况是h处于4～5之间［2］。

当│c│＞1 时，触发角选为使 cos α =0，由式(1)可求出:

式(9)中，当c＜h2/(h2-1)，会导出谐波电压峰值为负的错误结果。为此，可将式(9)修改为:

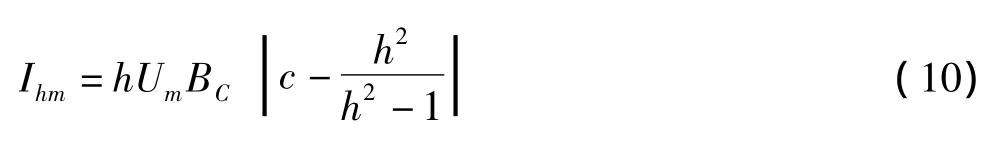
从而，h次谐波电流分量、基波电流分量峰值之比为:

文献［2］未考虑式(9)中Ihm为负的情况。

选择h=4.5，由式(8)、式(11)可画出比值 Ihm/I1m与c之间的关系，如图3所示。由图3及式(11)可知，当c=h/且在相应基波电压峰值处触发可使谐波电流峰值为零。其他情况下，谐波电流峰值均不为零。该条件原则上可以实现，但要增加相应的设备，实现较为麻烦，故实际工程中，一般均充电到电压峰值，并在相应基波电压峰值处触发仍能取得很好的效果。

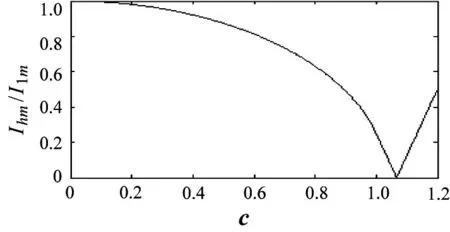
图3 谐波分量随电容器初始电压的关系

文献［1-2］对于投入谐波过程进行了大量的仿真，以说明投入时刻对谐波过程的影响。为简便，本文未再做仿真研究。

3 结语

1)TSC投入过程中的谐波电流分量的频率与自然频率相同。对电流分量峰值求小值点，可得到TSC最小谐波分量投入的条件，从理论上验证了相关文献关于投入过程的结论。

2)综合正、负半周的情况，电容器适当过充电并在系统电压峰值时刻触发可使谐波电流峰值为零。该条件的实现较为麻烦。实际工程中，可将电容器充电到电压峰值，并在系统电压峰值时刻触发，仍能取得很好的效果。

［1］姜齐荣，谢小荣，陈建业.电力系统并联补偿:结构、原理、控制与应用［M］.北京:机械工业出版社，2004.

［2］ABOUL-ELA M E，SALLAM A A，MCALLEY J D，et al.Damping controller design for power system oscillations using global signals［J］.IEEE Transactions on Power Systems，1996，11(2):767-773.

［3］WEN J Y，WU Q H，TURNER D R，et al.Optimal coordinated voltage control for power system voltage stability［J］.IEEE Transactions on Power Systems，2004，19(2):1115-1122.

［4］LEI X Z，LERCH E N，POVH D.Optimization and coordination of damping controls for improving system dynamic performance［J］.IEEE Transactions on Power Systems，2001，2(3):473-480.

［5］KULKAMI D B，UDUPI G R.ANN-based SVC switching at distribution level for minimal-injected harmonics［J］.IEEE Transactions on Power Delivery，2010，25(3):1978-1985.

［6］GOLE A M，SOOD V K.A static compensator model for use with electromagnetic transients simulation programs［J］. IEEE Transactions on Power Delivery，1990，5(3):1398-1407.

［7］TYLL H K，HUESMANN G，HABUR K，et al.Design considerations for the Eddy County static VAr compensator［J］.IEEE Transactions on Power Delivery，1994，9(2):757-763.

［8］MATHUR R M，VARMA R K.Thyristor-based facts controllers for electrical transmission systems［M］.New York:John Wiley ＆ Sons，Inc，2002.