HTS电动机定子开槽引起的转子涡流损耗计算

谭登洪，郑 军

（武汉电力推进装置研究所，武汉430064）

0 引言

高温超导（HTS）电机与传统电机相比具有体积小、重量轻、噪音低、效率高、制造成本低、营运成本低和维修较少等优点；此外，电机在运行中负荷作宽范围变化时，其高效率基本维持不变[1-4]。因此，HTS电机的研究对国防装备和国民经济建设都具有十分重要的意义。

HTS电机定子通常采用气隙（无槽）电枢结构形式，对于初次进行HTS电机研究的项目，基于项目研究目的、研究经费和进度的考虑，也可采用常规电枢形式，尽管这样与大容量电机的结构有一定差异，但可以集中精力解决转子低温电气工程方面的问题，同时也可起到减少超导带材用量的作用。

但HTS电机采用常规电枢结构形式时，定子开槽将带来气隙宽度的不均匀变化，从而产生了定子齿谐波。齿谐波和其它高次谐波一方面增大超导励磁区域垂直磁场，进而降低临界励磁电流的大小，对提高气隙磁密不利；另一更重要方面，齿谐波和其它高次谐波将会在转子结构件中产生涡流，这些损耗过大将引起HTS带失超，严重时将使HTS带熔融毁坏。为消除这些不良影响，通常采取在外转子加一个电磁阻尼屏来屏蔽这些谐波。另外，电磁阻尼屏还可消除负序及不对称的故障电流所产生的相对转子 2倍额定频率的磁场，和由故障电流所产生的跳跃变化[3]，因此需要对电磁阻尼屏的屏蔽效果进行精确的计算。

常用的电磁阻尼屏主要有图1所示的两种形式，支撑层由反磁性不锈钢制成，电磁屏由高纯铜制成。这两种转子电磁电磁阻尼屏蔽仅在结构上有区别，在屏蔽和阻尼效果上没有不同之处，夹心式机械强度更好，但制造也要麻烦些。另外，Lawrenson（1976年）等人建议采用一种不同质有孔的屏蔽系统。

本文以某HTS电机为例，推导了HTS电机电磁场数学模型，采用场路耦合时步有限元法对齿谐波以及电枢反应引起的高次谐波在转子结构件中产生的涡流损耗进行计算，计算了定子槽数和槽形对涡流损耗的影响，分析了电磁阻尼屏厚度与磁屏蔽效果的关系，同时计算了磁性槽楔对转子结构件涡流损耗的影响。

1 HTS电机数学模型建立有限元与分析

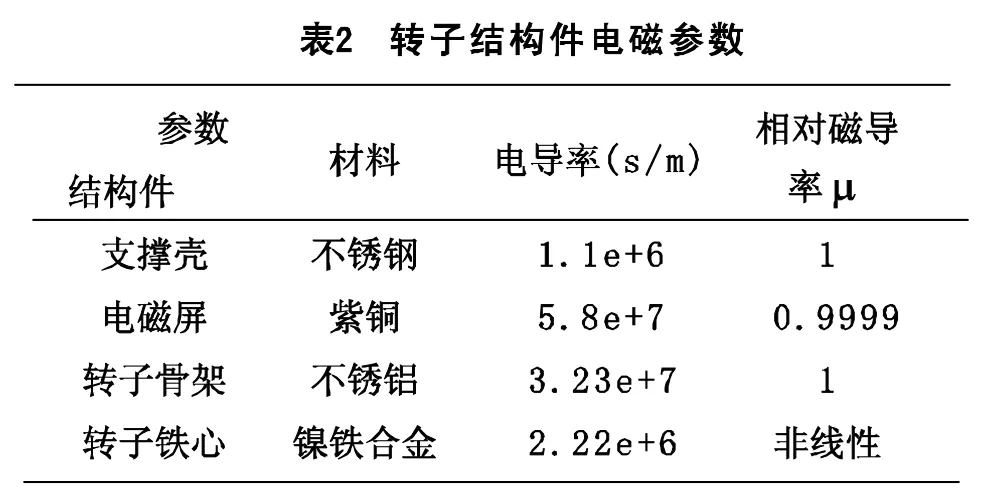
某HTS电机二维结构模型如图2所示，其运行原理和普通凸极同步电机类似。其转子与普通电机转子不同，主要由内外转子构成。其中外转子（电磁阻尼屏）由支撑壳和电磁屏构成，电磁屏主要起磁屏蔽作用，支撑壳主要起支撑作用，也有一定的磁屏蔽作用；内转子主要由励磁绕组、转子骨架和转子铁心构成，其中转子铁心主要起改善励磁绕组受力和提高气隙磁密等作用。这些转子结构件特别是内转子结构件的涡流损耗将对HTS励磁绕组正常励磁和电机的安全运行产生很大的影响。

因此，电磁阻尼屏蔽系统的设计必须保证在内转子结构件中产生的涡流损耗很微小或没有，以及超导线中的磁通变化不会使超导体失超。

为便于计算，分析时作下述假定：

1）磁场沿轴向不变，电机内磁场作二维场处理；2）定子磁屏蔽外表面没有漏磁，即磁力线平行于定子磁屏蔽外圆；3）定子磁屏蔽铁心磁导率各向同性。

根据对称情况，选择图2中电机一个极作为求解区域，在求解区域内矢量磁位A满足电磁方程[5]

下面分别就求解域中的各个区域进行分析。

1)定子铁芯、气隙和转子非励磁电流区域

忽略铁芯中的涡流效应，在铁芯和气隙中J＝0，对式(1)进行单元分析后，得到具有如下形式的矩阵方程

2)定子绕组区域

不考虑定子绕组中的涡流效应中，得定子电路方程如下:

把式（4）代入（3）得

式中,r—每支路绕组的电阻；Lσ1—支路绕组的端部漏感Sei—单元面积；Aei—该单元中磁动势的平均值；Ns—定子每个支路绕组中的串联导体数。将矢量磁位和电流对时间的导数用差分来代替，经过整理，得定子绕组区域的矩阵方程：

式（6）第一行与式（1）相对应，第二行与式（5）相对应，C11、C12、D21、D22分别由对应的系数项经单元合成而得。

3)励磁绕组区域

励磁绕组为超导磁体，无电阻，仅有直流电流if，因此有

4)总体合成方程

由以上分析，可以得到整个电机的场路耦合方程为

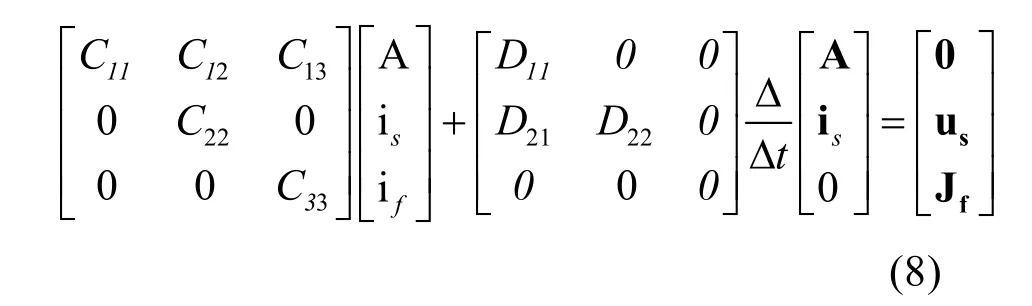
对上式进行时步有限元求解在时步法中，可用有限元复数模型来确定初值A(0)，I(0)。因为铁磁材料的磁导率具有非线性的特性，式（8）用牛顿——拉夫逊法求解，在每一步迭代中用不完全乔利斯基分解——共轭斜量法求解线性方程组。

2 转子结构件涡流计算

转子电磁屏蔽及其他结构件的涡流电流主要取决于定子齿谐波的大小，并且定子绕组正弦分布，因此转子表面的矢量磁势的空间分布可谓表示为[6]

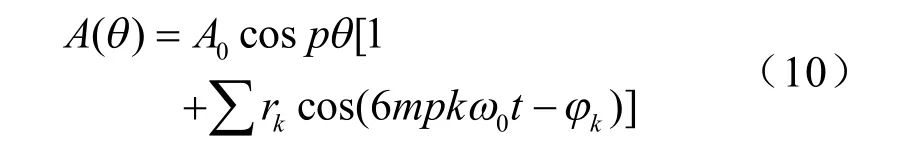
因此涡流电密可得到

由上式看出，产生的涡流是矢量磁势A0的系数值的函数，A0和rk与电机负载状况和导磁材料有关。

3 计算结果与分析

3.1 电机参数

某HTS电机主要结构和材料参数如表1和表2所示，选用图1（a）的电磁屏蔽结构形式。由于电磁屏的导电率越高厚度越厚其屏蔽作用越强，因此电磁屏也选用高纯铜。计算时，考虑到涡流电流是矢量磁位对时间的导数，所以时间步长取得越短计算结果越准确，这里时间步取为0.00001 s。

?

?

3.2 定子槽形结构对转子结构件涡流损耗的影响

3.2.1 槽数的影响

取电磁屏蔽厚度均为6 mm，计算定子54槽和72槽时转子结构件涡流损耗，计算时54槽额定励磁电流为60 A，定子电流89.2 A,72槽额定励磁电流为58 A，定子电流88.86 A。

?

算得额定负载时考虑转子涡流损耗的磁场分布如图4所示，涡流损耗值如表3所示，从中看出采用 72槽转子电磁屏蔽及内转子结构件涡流损耗大大减小，这由于采用72槽时，定子槽形变小，减小定子齿谐波的强度及其投入深度。所以该电机选用72槽。

3.2.2 槽形及槽楔性能的影响

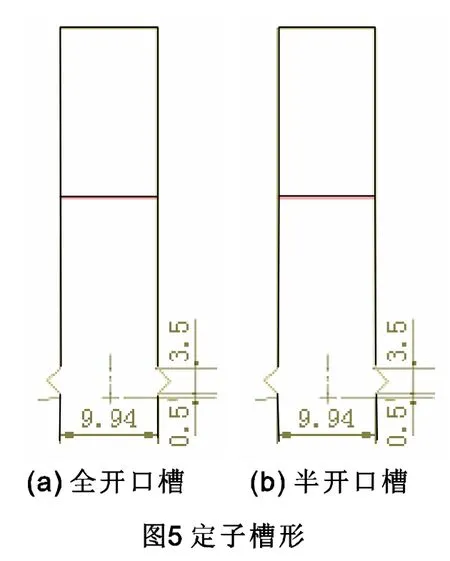
取定子72槽，电磁屏厚度为6 mm，根据式（11）算得不同槽形（图5）和槽楔材料时转子结构件涡流损耗如表4所示，其中磁性槽楔相对磁导率为10。

由表4看出：

1）定子槽形采用半开口槽时较之采用全开口槽，转子结构件涡流损耗较小，特别是非磁性槽楔时效果更为明显,涡流损耗减少了29.5%；

2）较之采用非磁性槽楔当采用磁性槽楔，转子结构件涡流损耗明显减小，全开口槽和半开口槽分别减少57.6%和44.3%。这是由于槽口宽较窄的半开口矩形槽和磁性槽楔，均能够有效地降低定子齿谐波强度，进而减小转子结构件涡流损耗。

3.3 外转子电磁屏蔽厚度的确定

这里在定子72槽，槽形为全开口槽，采用非磁性槽楔的情况下，以内转子结构件涡流损耗较小为设计目标，确定外转子电磁屏厚度。

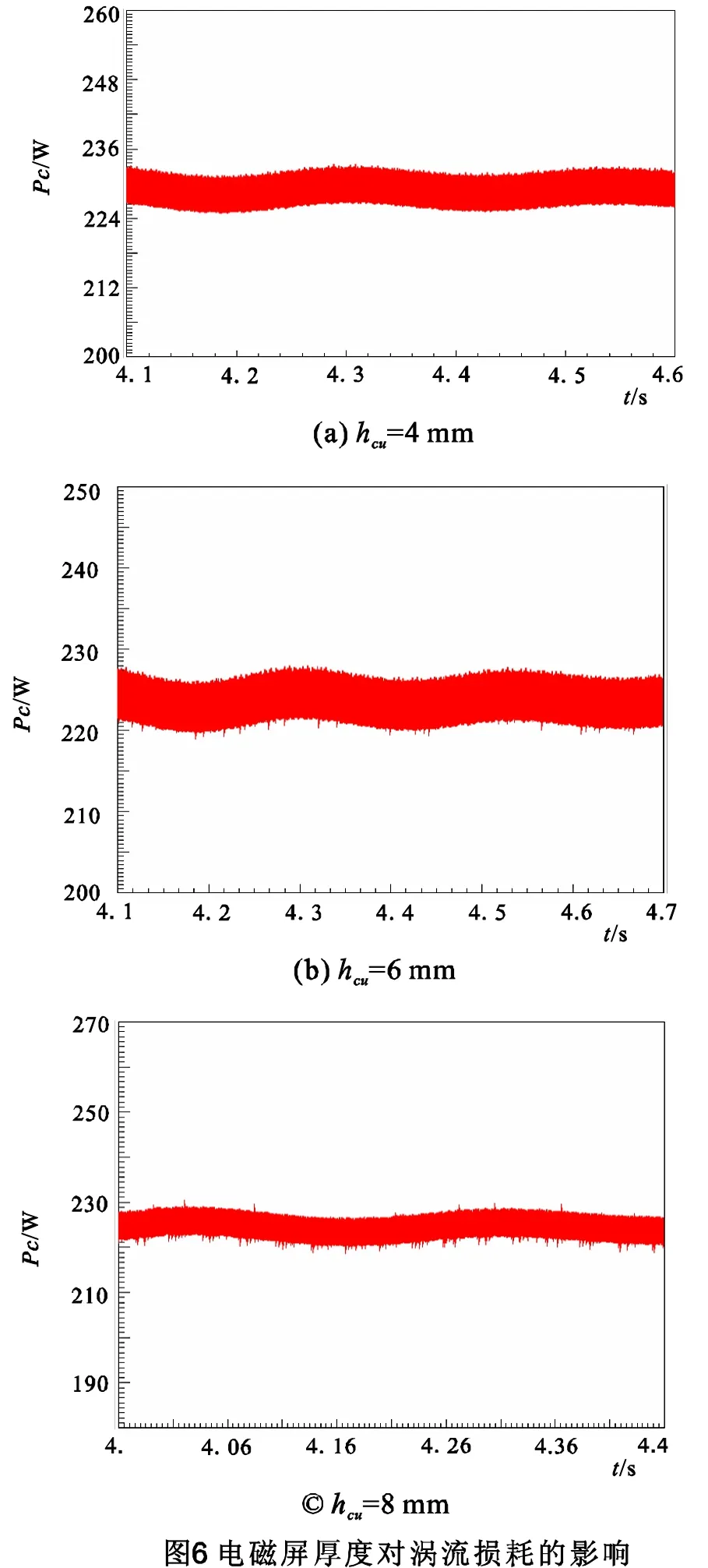
根据式（11）算得电磁屏蔽厚度hcu分别为4 mm、6 mm和8 mm时,转子结构件涡流损耗如表5所示。

?

从图6和表5看出：1）电磁屏越厚，内转子结构件涡流损耗越小；2）电磁屏厚度达到一定大小后，屏蔽效果提高很小，如hcu=6 cm或8cm时的各项涡流损耗基本相等，但二者较hcu=4 cm时内转子结构件涡流损耗减小了56.72%，已很微小。这是因为hcu=4 cm时齿谐波投入电机内转子在超导励磁线圈中将感应出较大的涡流损耗，而hcu=6 cm与hcu=8 cm两种情况下，定子齿谐波已基本被外转子的电磁屏蔽铜环屏蔽，不会透入到内转子中去，或即使透入也很弱。图7为hcu=6 cm时各结构件瞬时电密分布。

根据以上计算，对样机，定子采用72槽，磁性槽楔，槽楔厚度为 4 mm，考虑到转子内空间结构的大小，取电磁屏厚度为 6 mm，算得转子结构件涡流损耗总和为80 W。

4 结论

通过以上对定子开槽的HTS电机转子结构件涡流损耗的分析计算，得出如下结论：

1）定子槽口宽越小，由定子开槽引起的齿谐波强度越弱，对转子结构件涡流损耗越小，因此设计时应在下线工艺允许的范围内，尽量减小定子槽口宽；2）定子采用一定相对磁导率的磁性槽楔，可有效的减小齿谐波的影响，设计时应兼顾齿谐波的减小和漏磁增加两方面考虑，来确定磁性槽楔厚度，对本文计算样机磁性槽楔取其极限厚度4 mm为宜；3）电磁屏厚度一定时，选用电导率越高的非导磁材料屏蔽效果越好；电磁屏材料一定时，其厚度越大屏蔽效果越好，但达到一定厚度后，电磁屏厚度再增加，所起到的屏蔽效果提高很小，设计时需综合考虑屏蔽效果和转子内空间大小而确定电磁屏厚度。

[1]Biao,Gu Guobiao,Zhang Guoqiang,et al.Analysis and design of cooling system in high temperature superconducting synchronous machines [J].IEEE Transaction on Applied Superconductivity,2003,17(2): 1577-1560.

[2]MICHAEL Frank,PETER Van Habelt,PETER Kummeth.High-temperature superconducting rotating machines for ship applications[J].IEEE Transaction On Applied Superconductivity,2006,16(2): 1465-1468.

[3]SWARM S.Kalsi.Development status of rotating machines employing superconducting field windings[J].Proceedings of The IEEE,2004,92(10):1688-1704.

[4]SWARM S.Kalsi.Development status of superconducting rotating machines[J].IEEE PES Meeting,New York,2002: 27-31.

[5]VASSENT E,MEUNIER G,SABONNADIERE J C.Simulation of induction machine operation using complex magnet-dynamic finite elements[J].IEEE Trans on Mag,1989,25(4): 12-14.

[6]FREDERIC Bouillault and ADEL Razek.Eddy currents due to stator teeth in synchronous machine rotors[J].IEEE Trans on Mag,1984,20(5):1939-1984.