基于有限元边界元法的舰船开域空间静磁计算研究
2015-01-04夏建超徐正喜
左 超,耿 攀,夏建超,徐正喜
(武汉第二船舶设计研究所,武汉 430064)
0 引言
舰船磁场特征分析是舰船消磁的关键技术之一,随着舰船消磁技术的战术需求从单纯的水下防御向着立体化三维防御发展,舰船的远区磁场计算越来越受到科研人员的重视[1,2]。国外消磁工作者通过磁特征的基础理论研究并结合磁场模型的仿真技术,使得磁场建模尤其是远区磁场建模技术得到了重大突破[3]。国内舰船磁场计算方法也逐步从传统的磁偶极子、磁偶极子阵列、旋转椭球体阵列等算法向着基于现代计算机技术的微粒群、边界元、有限元等算法发展[4]。
有限元算法适合处理非线性、多介质问题,但随着求解域的增大,其计算量成倍增加,对于开域无限空间的求解并不适用。边界元法由于具有降维、高精度,又能良好适应无限域、半无限域和奇异场的要求,所以可以有效适用于开域问题[5]。本文采用有限元-边界元混合方法,将整个无限区域划分为有限元区域和边界元区域,通过舰船空间静态磁场的计算仿真,验证了该方法的正确性、高精度及高效性。
1 舰船无限空间磁场计算方法
1.1 有限元算法
舰船在地磁场作用下会造成空间磁场畸变,可以看作是静态弱磁场对铁磁物质的静态可逆磁化过程。对舰船外部空间磁场分布的研究可以归结为一个开域空间的静态磁场问题。
在静态磁场问题的求解中可以引入标量磁位φ,磁场强度表示为

其中:-gradφ是的无旋分量( 即rot(-gradφ)=0),而为有旋分量或为零。有限元法静磁场标量模型的通用求解方程如下

有限元法就是将求解区域细分为大量的有限单元区域(如三角形),在每个单元区域中建立(2)式中方程。可以通过加勒金法或直接由目标能量寻找法获得定义域内场的分布函数,此函数根据单元的节点取极值,然后将所有同节点有关的单元积分,给出一个设定节点磁势(法线方向)多项式变分。这样,每个节点产生一个等式,从而得到大量的联立方程。解出这些方程,就可以确定每个节点的磁势。对于磁特征的求解问题不可避免地要采用三维场的方法,但是采用标量磁势方程可以大大地减少未知参数的数量,因为每个节点只需一个变量,而不是像矢量磁势方程那样需要三个变量[6]。由于舰船几何模型能很全面的反映舰船实际构成,因此采用有限元法可较准确地计算舰船近区磁场。
舰船近区磁场有限元计算流程依次是物理模型的选取,建立舰船的几何模型、网格剖分、设置物理属性,其中包括材料属性、机械属性、外部电路、再对求解进行相应的算法选取和参数设置,求解完后就进行相应的后处理。
1.2 边界元算法
边界元法的基本原理是根据场源周围闭合曲面的外法线方向的方向导数求得闭曲面上的标量磁位,进而推算出闭曲面外周围空间各点的标量磁位分布,进而可以推算出空间各点的三分量磁场值。假设有一闭合面S将磁场之“源”完全包于其内,如下图1所示舰船包络面示意图,称S为边界面,S之外的空间为场域V。

图1 舰船包络面示意图
为研究有限场域内的磁场分布,设u为标量磁位,如果在边界面S上,u或(u的法向导数)是已知的,则场域中任意一点的u都是唯一存在的。由边界上u或的分布求场域中u的问题称为磁场边值问题。设舰船包络面外的区域V(即远区换算点)为待换算的区域,舰船包络面S为V的边界面,设V中任一点为M,包络面上任一点为M0,则由格林第二公式,可推导出M0处的磁位值为:

式中r为M0至变点M的距离,为沿边界面外法线方向的方向导数。
2 仿真算例
本文以电磁场仿真软件FLUX为基本的仿真平台进行舰船开域空间磁场计算,法国CEDRAT公司的FLUX软件被广泛应用于舰船磁场的计算及消磁绕组布置的设计[8,9]。FLUX封闭域求解基于有限元算法,可进行舰船的复杂结构、薄壳超大纵横比、多介质界面耦合仿真计算,同时还可以在无限区域耦合多类型的边界条件,以求解舰船远区磁场。
第一步,根据计算需求,选择FLUX软件的静态磁场三维求解器Magneto Static 3D进行舰船静态磁场仿真计算。
第二步,通过造型系统对舰船的主要壳体部件进行几何模型建模,由于曲面造型难以进行网格剖分,该模型对舰船曲面进行了大量简化,肋骨、设备、上层建筑也进行了简化处理,FLUX建模最大的特点是对于舰船壳体部分的简化处理可以采取蒙皮模型,而非实体模型,该方法的好处是可以减少剖分网格量,也方便求解薄壳模型。如图2所示,简化舰船模型长100米,宽20米,高10米。可以看到舰船位于双层空气包以内,空气包外壁边界用于模拟开域问题来求解无穷远处的磁场问题。

图2 简化舰船几何模型
第三步,模型的网格剖分。舰船形状特殊,结构复杂,因此在剖分的过程中尽量使用只有四面体单元的剖分器,但不宜采用自动剖分模式,手动设定合适的网格大小,是保证求解精度的关键。如图3所示,针对本文模型大小,剖分网格边长设定为空气包层 5000 mm,船模部分 1000 mm。为了满足计算精度要求,剖分的过程中要保证双层空气包之间达到有效的网格量(大于 3层剖分单元)[10]。

图3 舰船网格剖分图
第四步,设置物理属性。简化舰船模型中的船体材料设置为两种磁导率,壳体部分相对磁导率设定为100;甲板部分相对磁导率设定为300,厚度均为50 mm;其余部分全部设定为真空区域。为了方便分析磁场结果,外加磁场激励设定为地磁单一分量,即武汉地区水平磁场强度34000 nT,空间均匀分布,舰船航向为北航向。
第五步,求解及后处理。经过计算求解完成之后,即可进行后处理,如图4所示,可查看舰船表面的磁场分布云图。此外还可以在远区空间增加后处理测试线/面,查看开域空间静磁分布。

图4 舰船表面磁场分布云图
3 结果分析
为了验证有限元边界元混合方法在求解舰船开域空间磁场过程中的高效性,我们使用同样的仿真模型,比较单纯使用有限元和有限元边界元混合方法求解过程中的计算资源消耗,如表1所示,有限元边界元混合方法可将整个求解时间降低81%,极大提高舰船远区静态磁场的求解效率。

表1 两种算法求解效率对比表
同时,为了验证有限元边界元混合方法在求解舰船开域空间磁场过程中的精度,我们建立了磁偶极子模型,将上述舰船模型等效为11个纵向均匀分布的磁偶极子阵列,通过100 m高度数据求解偶极子磁矩,然后推算其他高度磁场强度。求解结果对比如下图5~图8所示。

图5 FLUX仿真与磁偶极子结果对比(上方50m)
从图5结果可以看出,有限元边界元混合方法能够在近场区域保证更为丰富的舰船磁性特征,相比磁偶极子算法精度更高。从图6-图8结果可以看出,有限元边界元混合方法同样能够在远区保证可靠的求解精度,与磁偶极子阵列模型相比,误差控制在2%以内。
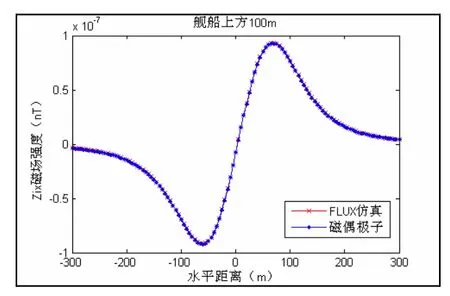
图6 FLUX仿真与磁偶极子结果对比(上方100m)
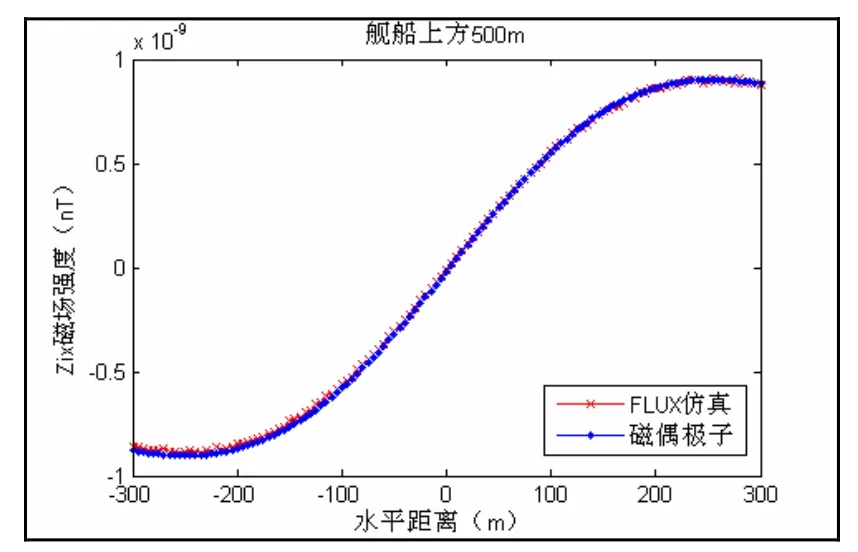
图7 FLUX仿真与磁偶极子结果对比(上方500m)

图8 FLUX仿真与磁偶极子结果对比(上方1000m)
4 结束语
本文分析了有限元边界元混合法在舰船开域空间静态磁场求解问题中的适用性,并以电磁场分析软件FLUX作为仿真计算平台,通过有限元边界元混合法对舰船开域空间静态磁场进行了仿真计算,建立了舰船几何模型,进行了网格剖分,并深入探讨了参数设置方法,得到了仿真计算结果。在舰船开域空间静态磁场求解问题上,该方法具备高效、高精度等优点,可应用于工程实践。
[1]粟有鼎.舰船磁防护与声防护[M].北京: 国防工业出版社,1985,97-99.
[2]刘大明,刘胜道,肖昌汉,周国华,王昭.舰艇闭环消磁技术国内外研究现状.船电技术,2011,31(10):6-9.
[3]Jeung G,Yang C S,Chung H J,et al.Magnetic dipole modeling combined with material sensitivity analysis for solving an inverse problem of thin ferromagnetic sheet[J].IEEE Transactions on Magnetics,2009,45:4169-4172.
[4]连丽婷,肖昌汉,刘胜道.基于微粒群算法的薄钢板两侧磁场推算中的位置优化[J].上海交通大学学报,2010,44(7): 975-979.
[5]王占辉,高俊吉.一种开域静磁场双标量位混合有限元边界元法研究[J].船电技术,2013,33(06):19-21.
[6]汪家骅.正则化技术在舰船磁场建模逆问题中的应用[J].水雷战与舰船防护,2010,18(4): 1-5.
[7]倪光正,杨仕友,钱秀英,等.工程电磁场数值计算[M].北京: 机械工业出版社,2004: 237-241.
[8]Birsan M.User Experience: Defence research for development Canada[J].Flux Magazine,2006,50: 11.
[9]姜智鹏,庄飚,关涛,母海方.基于FLUX软件的舰船磁场计算[J].船电技术,2010,30(12): 17-20.
[10]张超,高立娥,刘卫东,刘铎.FLUX(3D)在舰船磁场方面的应用研究[J].声学技术,2011,30(4):110-113.
