海浪谱的二维仿真及验证*

于龙飞，张亚群

（1. 广州航海学院，海运学院，广州 510725；2. 中国科学院广州能源研究所，中国科学院可再生能源重点实验室，广州 510640）

海浪谱的二维仿真及验证*

于龙飞1†，张亚群2

（1. 广州航海学院，海运学院，广州 510725；2. 中国科学院广州能源研究所，中国科学院可再生能源重点实验室，广州 510640）

海浪仿真是海洋工程的热点话题。本文总结了一种可以适应于各种随机波浪谱来仿真海浪环境的方法，利用C语言将该方法转换为过程简单、编写方便的计算机程序得到大量仿真波浪数据，并作为造波机输入数据，通过实测数据检验仿真结果。试验证明，采用文中提出的数值方法，采集模拟波高数据利用相关函数法进行频谱估计，得到的模拟谱和靶谱误差较小。该数值仿真方法在海浪仿真上具有实际应用价值。

海浪谱；随机数；靶谱；频谱估计

0 引 言

海洋工程的研究基础建立在对海浪的研究之上，海浪的仿真为在实验室展开海洋工程研究提供了基本条件。海浪仿真的准确度越高，实验室试验与实海况试验越接近，越有利于提高试验模拟的精度、试验数据的可信度。海浪是不规则的、随机的，通常以海浪谱的形式描述海浪的随机过程，以达到统一的标准便于建模仿真等相关的研究分析。经过长期的实际观测研究，研究人员已经总结出各种海浪谱的经验公式。这些海浪谱通常是以频率为自变量的函数，无法直接应用于实验室造波试验中。把这些海浪谱由频域转化为时域，再应用于海浪仿真中，是目前常用的海浪仿真方法[1]。但此类方法大多比较繁杂且具有局限性，无法适应于不同的海浪谱。本文概括了一种系统的海浪数值仿真方法，克服了传统的波浪模拟中采用单一海浪谱为目标、试验过程中多次输入多次生成大量模拟数据所导致的局限性，改进了循环嵌套程序造成的运算量过大的问题。该方法将波谱分析−波谱模拟−波浪生成集成为一个整体，适应于各种类型波浪谱的模拟，加快了模拟的速度，提高了模拟精度。

本文虽然以PM谱为例，但各个参数的取值范围较宽，使该方法不仅适用于成熟的波浪谱，而且适合一般海域的观测谱。采用计算机C程序语言使仿真过程程序化之后，该方法将更加方便。采集模拟海浪的数据，采用相关函数法进行频谱估计，验证仿真结果与实际值的一致性。

1 海浪数值仿真方法[2-6]

1.1 海浪谱

经分析，总结出国际上规定的海浪谱都符合以下公式[2]：

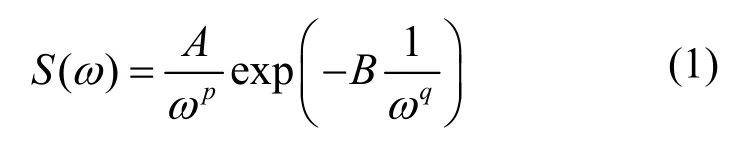
其中，指数p通常取4～6，q为2～4，A和B中包含风要素（风速、风时、风距）或波要素（波高、周期）作为参量。海浪可以看作一个各态历经的平稳随机过程。通常可以把一组不规则波浪分解成多个不同周期、不同波长、不同波幅和不同随机相位的相同传递方向的余弦波叠加而成。式（2）为任意时刻波面相对静水面高度的表达式：

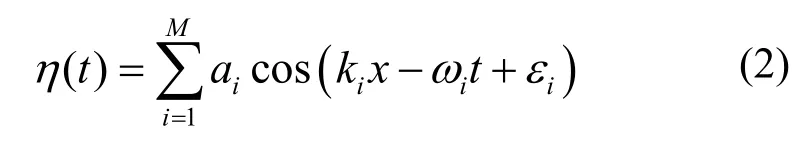
其中：ai为t时刻第i个组成波的振幅；ki、ωi为t时刻第i个组成波的波数和圆频率；x为t时刻波面坐标轴的横坐标值，通常x轴的正方向沿着波浪传播方向；εi为t时刻第i个组成波的初相位，在频域与时域转换时，一般推荐取分布于（0, 2π）范围内的随机数。

1.2 波浪叠加法

用波浪叠加法进行海浪仿真，主要是分解波浪的频谱，应具有以下几个步骤：

（1）频率范围的选取。根据各方面资料显示，海浪模拟的频率范围一般以表1为参考。表中列出的仿真频段为欲模拟的对象谱（靶谱）S(ω) 能量集中频段，其余部分可以忽略不计。根据试验要求的有义波高H1/3选定仿真频率段，确定最低频率（ωL）、最高频率（ωH）的值。通常频率选择越宽，模拟的波浪所包含的能量越大，仿真结果越逼近实际值。但是频率太宽会造成计算量过大，计算速度较慢，且在离谱峰频率较远的频率区域中的数据对结果影响较小。

表1 不同海况仿真频段Table 1 Simulation frequency zones under different sea conditions

（2）划分频率区间。一般划分频率区间的方法分为等分频率和等分能量两种方法，这里采用等分能量法。定义累积谱为：

（一）预防措施 仔猪副伤寒的预防，应特别注意初春时节温度变化不定，做好仔猪圈舍的保暖，中午仔猪可适当晒太阳；圈舍保持清洁干燥，食槽要经常洗刷，粪便发酵处理。加强饲养管理，初生仔猪应争取早吃初乳，并提前补料，以防乱吃脏物，断奶分群时，不要突然改变环境，猪群尽量分小一些。仔猪断奶前后（建议28日龄），口服仔猪副伤寒弱毒冻干苗进行预防。较大规模养猪场发病后，应将病猪隔离治疗，猪舍彻底消毒。未发病的猪可用药物预防，在每吨饲料中加入金霉素100 g或氟苯尼考（50～100 ppm），可起较好的预防作用。

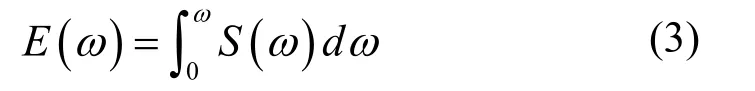
等分能量法将所模拟的谱的能量等分为M份，即分为M个波组成，由i=1, 2, ··, M表示。分界频率ωi可以由下式计算：

其中，m0为谱的零阶矩，m0=A/(4B)。这里要求对象谱S(ω)为可积分，如P−M谱和B−M谱等，由式（1）和式（3），p=5，q=4，可得：

将E(∞)=A/(4B)和式（5）代入式（4）中得：

当谱形无法积分时，通过数值积分计算累积谱E(ω)，得出一个关于 ωi的算式f(ωi)，与式（4）一起得到f(ωi)=im0/M，解出此式得ωi。

为了避免长时间的模拟波形可能出现重复现象，第i区间的代表频率可用下面算式计算：

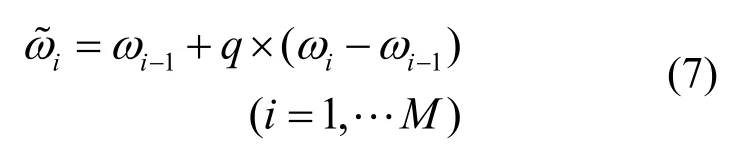
式中，i=1, 2, ··, M，表示第i个频率的波；q为分布在（0, 1）之间的随机数。

（3）初相位的确定。随机初相位εi应在（0，2π）之间随机分布。计算式为：

式中f也为（0, 1）之间的随机数，初相位的随机性决定了波浪重复性，故随机数f的选取要注意质量。

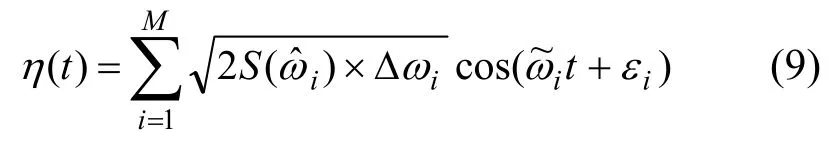
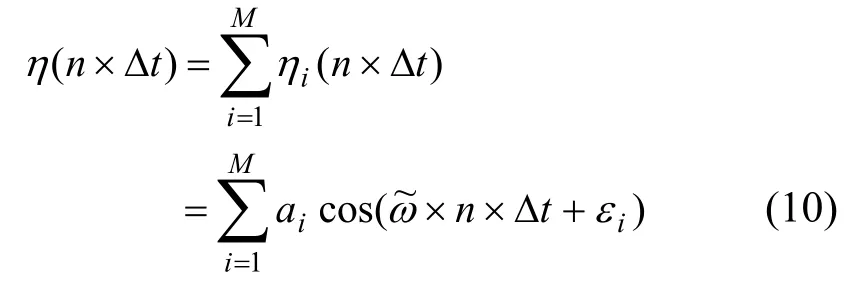
由上式可知，即当M=50、n=1时，可得50个不同的ai、50个不同的εi，由此得到50个不同的ηi(Δt)。累加这50个ηi(Δt)，即可得到t=Δt时的波面高度η(Δt)。依此类推可以计算出不同时刻的波高值，输出给造波机就可以模拟出靶谱。

1.3 编程实现

上述对海浪谱仿真过程的数值分析，可以通过调用C语言函数库中现成的函数编程得到基本实现。某些情况下，只需做一些数学处理。例如，调用函数int random（int num），可以得到0～num之间的随机整数。如要得到上述要求的0～1之间的随机数，程序可以写成：

在对不同海浪谱的海浪仿真时，由于对频谱的处理过程都用波浪叠加法处理频率计算，因此在编写一个外部函数供不同频谱仿真时调用，将大大减少计算机的计算量。并且，数值分析得到的波浪时域上的仿真数据（即模拟时输入波高数据）可以存储在同一个动态数组当中，节省了程序的内部存储空间。以PM谱为例介绍程序结构[7]。

2 仿真结果的验证方法

仿真结果的验证是对仿真结果的定量和定性分析，确定其与理论结果一致性的程度[8]，同样也是对仿真数值分析方法正确与否的一种检验。本文使用上述仿真方法造波，用浪高仪在定点位置实时采集波高数据，再进行波谱分析得到模拟的波谱，通过与靶谱进行对比分析得到验证结论。

通常采用的谱分析有多种方法，如相关函数法、快速傅里叶变换法（FFT）、最大熵法等谱估计的方法。由于FFT需要采集的数据实际是一个完整的周期，这在实际操作中很难达到。而最大商法是建立在相关函数法的基础上，虽然相关函数法需要在较大区间内作积分求解，由于计算机的计算能力较强，在研究初期本文采用相对简单的相关函数法。该方法得到的频谱光滑度不高，利用加窗平滑处理，提高谱的质量。一般加窗处理有两种选择，一种为哈明（Hamming）窗，另一种为哈宁（Hanning）窗。

3 结果验证及分析

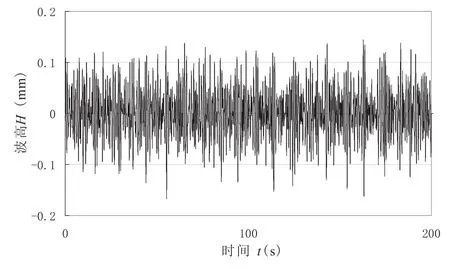
图1 随机海浪仿真结果Fig. 1 Simulation results of random wave

图2为实际采集的模拟波高数据，采集频率为50 Hz，采集时间为200 s。根据图中的实测波浪数据统计，H1/3=0.219 9 m，误差为0.019 9 m。

图2 采集海浪波高数据Fig. 2 Gathering data of wave height

采集数据后进行波谱分析得到波谱曲线（蓝色曲线）与靶谱曲线（红色曲线）比较如图3所示。图中横坐标表示圆频率（w=2πf），纵坐标表示谱密度函数 [S(ω)]。

图3 模拟谱与靶谱比较Fig. 3 comparison of simulate spectrum and target spectrum

对比图3中的两条曲线，模拟的海浪谱与靶谱比较相近。靶谱的谱峰密度为0.001 108 m2s、谱峰频率为2.355 rad/s，实测谱谱峰密度为0.001 255 m2s、谱峰频率为2.355 rad/s。两者谱峰频率没有误差，但是谱峰密度之间差距稍大。其中，造波机的造波精度、采样点数有限、浪高仪采样精度等都是造成误差存在的主要原因。利用迭代的数值处理方法，可以减小两者之间的误差，并随着迭代次数的增多，误差将越小。

4 结 论

本文总结了一套条理清晰、步骤明确的方法仿真海浪场环境，可以应用于绝大部分海浪谱，具有通用性，同时利用C语言将该方法编写成通用的程序，又使海浪谱的频域至时域转化可以利用计算机来完成，使整个仿真过程更加便捷精确，为了进一步验证仿真结果，采集模拟波高数据后通过频谱分析，对比模拟谱和靶谱，验证了该方法的准确性。

[1] 郑茂琦, 马春翔, 王志波, 等. 基于海浪谱的海浪模拟的改进[J]. 系统仿真学报, 2014, 36(2): 369-375.

[2] 俞聿修. 随机海浪及其工程应用[M]. 大连: 大连理工大学出版社. 2000.

[3] 王立军. 船舶动力定位海浪环境的实时仿真与海浪谱分析[J]. 华东船舶工业学院学报, 2001, 15(1): 48-51.

[4] 李远林. 近海结构水动力学[M]. 肇庆: 广东理工大学出版社. 1999.

[5] 文圣常. 海浪理论与计算原理[M]. 北京: 科学出版社. 1984.

[6] 徐德伦, 于定勇. 随机海浪理论[M]. 北京: 高等教育出版社. 2001.

[7] 张凤均. Labwindows/CVI开发入门和进阶[M]. 北京:北京航空航天大学出版社. 2002.

[8] 杨惠珍, 康凤举, 褚彦军, 等. 基于海浪谱的随机海浪仿真及验证[J]. 系统仿真学报, 2005, 17(10): 2324-2326.

2D Wave Simulation and Validation Based on Ocean Wave Spectrums

YU Long-fei1, ZHANG Ya-qun2
(1. Guangzhou Maritime Institute, Maritime, Guangzhou 510725, China； 2. CAS Key Laboratory of Renewable Energy, Guangzhou Institute of Energy Conversion, Chinese Academy of Sciences, Guangzhou 510640, China)

Wave simulation is a hot topic of Ocean Engineering. This article summarizes a method that can adapt to a wide range of random wave spectrums to emulate the waves environmentally. The method is converted to computer programs which are simple and convenient by language C and compute a large number of data used as data source to wave maker. The simulation result is verified by the experiment data. The test shows that the error between the analog spectrum and the target spectrum is lowest by using the numerical method presented in this paper. The acquisition of analog wave height data are used to estimate the spectrum by correlation function method. The numerical simulation method has a practical application value in the wave simulation.

wave spectrum； random number； target spectrum； evaluation of frequency spectrum

TK79；TP391.9

A

10.3969/j.issn.2095-560X.2015.03.009

2095-560X（2015）03-0214-04

于龙飞（1981-），男，博士，讲师，主要从事海洋工程、船舶及新能源方面的研究。

2015-04-21

2015-05-08

广州航海学院强校项目；中国科学院重点实验室基金（y407j31001）

† 通信作者：于龙飞，E-mail：yulongfei118@163.com