新型脆性因子及其在泥页岩储集层预测中的应用

刘致水，孙赞东

（1.中国石油大学（北京）地质地球物理综合研究中心；2.中国石油大学（北京）油气资源与探测国家重点实验室）

新型脆性因子及其在泥页岩储集层预测中的应用

刘致水1,2，孙赞东1,2

（1.中国石油大学（北京）地质地球物理综合研究中心；2.中国石油大学（北京）油气资源与探测国家重点实验室）

针对油气勘探中普遍使用的脆性因子的缺点，构建了两个新的相对脆性因子（弹性参数脆性因子和矿物脆性因子），以准确预测脆性泥页岩的空间展布。弹性参数脆性因子利用测井、地震得到的弹性参数（弹性模量和泊松比）评价储集层脆性，这些参数能够反映储集层原位物理性质；根据弹性参数脆性因子确定泥页岩中主要矿物的脆性系数，构建与每种矿物脆性系数及体积分数相关的矿物脆性因子。所构建的两个脆性因子有一定的理论优势并能够较合理地对测井、叠前地震资料反演结果进行解释。根据富有机质泥页岩岩石物理模型，建立矿物-弹性参数-脆性因子的岩石物理量版，对测井资料进行分析以得到优质脆性泥页岩的弹性参数特征，并将其应用于解释叠前地震资料反演结果，得到优质含气脆性泥页岩的空间分布范围，所预测的优质含气脆性泥页岩分布与测井资料对应较好。图12表2参18

相对脆性因子；矿物脆性因子；弹性参数脆性因子；岩石物理量版；泥页岩

0 引言

在致密泥页岩储集层开发中，水力压裂是提高油气采收率的主要技术，也是常规技术。对储集层的可压裂性进行评价，确定较好的压裂位置，对压裂成功与否至关重要。脆性是评价岩石可压裂性的重要参数，目前还没有统一的定义。在材料科学中，脆性材料定义为在应力作用下，不发生明显的形变就发生断裂的材料，即在断裂前基本不因形变吸收能量，比如陶瓷；塑性材料定义为在应力作用下，发生明显形变才断裂的材料，比如纯度较高的铁。材料科学中对脆性的研究较深入，评价方法也较多[1-3]，这类方法基本都是根据实验室测量的强度（抗压强度，抗拉强度）、硬度、坚固性数据定义脆性，其中基于强度的脆性主要利用抗压和抗拉强度的差异评价脆性，认为抗压强度和抗拉强度差异越大，脆性越强；基于硬度或坚固性的脆性评价方法，其原理是考虑岩石在宏观、微观硬度、坚固性方面的差异。对于油气勘探，由于地下岩石及储集层的非均质性，以及岩心的昂贵，使得针对性的实验室脆性测量研究效率低下；储集层地球物理学家建议使用岩石中脆性矿物含量[4]及弹性参数[5-8]来构建脆性评价参数（矿物脆性因子和弹性参数脆性因子）并表征储集层的相对脆性程度（笔者认为，这些办法以及本文中所建立的关系求得的脆性都不是岩石的绝对脆性程度，而只是一个相对的、仅具指示意义的脆性程度，因此称为相对脆性），这种办法实用性强，应用效果也较好。其中，利用脆性矿物含量评价岩石脆性的理论依据是不同的矿物具有不同的脆性程度，脆性矿物含量高的岩石其脆性程度亦高；弹性参数表征脆性的理论依据则是材料的应力-应变关系，即利用表征径向形变量的弹性模量和表征横向形变量的泊松比表征脆性，高的弹性模量与低的泊松比代表高的脆性程度。上述两种方法均存在缺陷，其中矿物脆性因子没有考虑岩石中不同矿物之间的脆性差异，而弹性参数脆性因子又存在一定的理论缺陷。本文针对上述问题，提出两个修正的相对脆性因子，并利用富有机质泥页岩岩石物理模型建立矿物-弹性参数-脆性因子岩石物理量版，并对叠前地震资料进行分析，获得优质脆性泥页岩储集层的空间分布。

1 理论与方法

1.1 弹性参数脆性因子构建

岩石的弹性是岩石中物质组成、结构、孔隙、流体在一定温度压力环境下的综合响应，尤其是通过测井、地震等手段测量得到的弹性信息，反映的是储集层内部特征在原位环境作用下的综合响应。因此，利用弹性参数构建脆性因子，可以为利用测井、地震资料进行储集层脆性评价提供手段。而岩石弹性参数与脆性在物理意义上具有明确的联系，如图1所示，当一个长为L0、横截面直径为W0的圆柱体受到径向拉力σzz时，会在径向形成拉伸形变ΔL，同时在横向形成压缩形变ΔW，径向拉伸形变系数为ezz=ΔL/L0，横向压缩形变系数为err=ΔW/W0。据此可计算弹性模量和泊松比，弹性模量E=σzz/ezz，为径向拉伸力与径向形变的比值；而泊松比ν=-err/ezz（拉伸为正，压缩为负），为横向形变系数与径向形变系数的比值。脆性材料定义为在一定应力作用下，发生较小的形变即发生断裂的材料，即在σzz一定的情况下，材料断裂时ezz越小脆性越高，即弹性模量越大材料的脆性越大；通常物体的横向变形系数小于径向变形系数，且当泊松比较大时，岩石在横向上较容易发生形变，即泊松比越小，脆性越高。因此，利用弹性模量和泊松比可以评价岩石脆性，不同的弹性模量和泊松比的组合表示岩石具有不同的脆性，弹性模量越大，泊松比越低，岩石的脆性越大，这是使用弹性模量和泊松比表征脆性程度的物理原理。

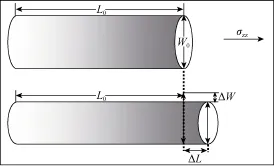
图1 物体弹性应力-应变示意图

基于以上认识，一些储集层地球物理学家利用弹性参数构建脆性因子[5-8]，主要有3种方法：①使用弹性模量正归一化，泊松比反归一化后的加权平均表征脆性[6]，如公式（1）所示；②使用弹性模量与泊松比的商表征脆性[7-8]，如公式（2）所示；③使用拉梅系数表征脆性[7]，如公式（3）所示。对比这几种脆性计算公式可以发现，使用弹性模量和泊松比表征脆性的物理意义较为明确，与物体的应力-应变关系直接相联系，而拉梅常数没有明确的物理意义；公式（1）与（2）同时考虑了弹性模量和泊松比，即径向形变和横向形变的能力，且都满足弹性模量越大、泊松比越小，脆性因子数值越大的规律，但是公式（1）中弹性模量和泊松比的权重都为0.5，即认为两者对岩石脆性程度的贡献等同，此为经验认识，不具有理论依据；公式（2）不涉及弹性模量和泊松比权重的问题，但是，由于弹性模量数量级较大（一般矿物为1～100 GPa量级），而泊松比数量级较小（0～0.5），从而导致该公式数值不稳定。

本文结合公式（1）与（2），提出一种基于弹性模量和泊松比的新弹性参数脆性因子，如公式（4）所示，它采取公式（2）的形式，结合公式（1）的特点，通过数据的归一化提高了稳定性：

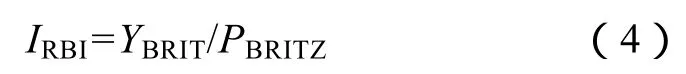
其中，YBRIT=(E-0)/(10-0)=0.1E，PBRITZ=(υ-0)/(0.4-0)= 2.5(υ-0.4)，与公式（1）中泊松比采取反归一化不同，此处是正归一化。

图2为4种弹性参数脆性因子的对比图，对比图以包含矿物成分、弹性参数、脆性因子的岩石物理量版方式给出，量版由岩石物理模型正演得到，模型及量版的建立在本文第2节详细论述。图中多边形的4个端元点分别代表纯的黏土、方解石、石英以及干酪根，其参数值见表1，多边形中每一个色块都代表一种矿物组合情况下的弹性参数以及脆性因子。将测井资料中的砂岩、砂质泥岩、泥岩数据投入量版。可以看到，图2a中的脆性因子在方解石端元点附近突变；图2c中黏土与方解石的理论脆性值近似，对实际资料解释时，砂质泥岩与泥岩的脆性基本一致，不符合地质认识，即公式（3）对于黏土、方解石以及砂质泥岩之间的脆性差异不能合理解释；图2b、2d的变化趋势较为合理，且能够较好地描述实际数据的变化趋势，即砂岩的脆性高，纯泥岩的脆性最低，当砂岩含泥后，其脆性降低，在黏土理论值附近，但是，图2b所对应的公式（2）数值不稳定。因此，图2d所代表的公式（4）在理论上有优势，且能够较好地利用实际测井资料进行岩石脆性程度解释。

图2 4种弹性参数脆性因子对比图

表1 不同公式计算的几种主要矿物的弹性参数与矿物脆性因子

对4种弹性参数脆性因子的区分能力（敏感性）进行分析，评价其区分硅质页岩（石英含量25%，黏土含量75%）与钙质页岩（方解石含量25%，黏土含量75%）的能力。此处区分能力指两种物体同一表征参数的差异：

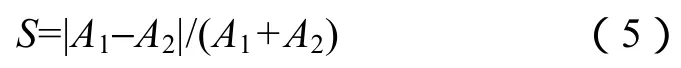
图3为4种弹性参数脆性因子敏感性的比较，可见新脆性因子的区分能力优于其他3种。

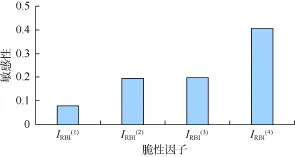
图3 不同脆性因子对硅质页岩和钙质页岩的敏感性比较（IRBI(1)，IRBI(2)，IRBI(3)和IRBI(4)分别为公式（1）、（2）、（3）、（4）计算的脆性因子）

1.2 矿物脆性因子构建

弹性参数可以较好地表征岩石的脆性，但是在某些条件下，如测井没有横波资料，或岩心有矿物成分鉴定数据而没有测量弹性参数的情况下，无法使用弹性参数脆性因子。针对这一情况，前人提出使用岩石中脆性矿物与塑性矿物的体积分数来表征脆性，最常用的为公式（6）和公式（7）[4]：

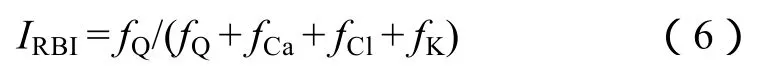
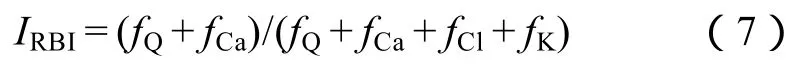
该方法将岩石矿物分为脆性矿物和塑性矿物两种，计算过程中考虑了脆性矿物对岩石脆性的贡献，其中，（6）式将石英作为脆性矿物，（7）式将石英和方解石作为脆性矿物。方法的缺陷是没有考虑不同矿物对脆性贡献程度的差异，比如（7）式认为石英与碳酸盐对脆性的贡献是相同的，都仅与其体积分数一致。显然，石英与方解石的脆性是不同的，同理，不同矿物对塑性的贡献也是不同的。

本文根据新建立的弹性参数脆性因子，计算页岩组成矿物的脆性程度，认为石英的脆性最高，干酪根的脆性最低，因此，假定石英的脆性系数为1，干酪根的脆性系数为0，归一化得到页岩中主要矿物（本文给出14种）的脆性系数。如图4所示，归一化后的脆性系数显示，脆性程度从高到低依次为石英、白云石、方解石、钠沸石、沸石、硬石膏、条纹长石、斜长石、岩盐、正长石、墨西哥湾黏土、混合黏土、干酪根、高岭石。在此基础上，构建与每种矿物的脆性系数相关的脆性因子，如公式（8）所示。

新脆性因子考虑了每种矿物脆性程度的不同，相较于公式（6）、公式（7）具有明显的理论优势。图5为3种岩石脆性因子对比图，同样以岩石物理量版的方式给出。可以看到，图5a、5b都将岩石矿物组成大体划分为脆性和塑性两部分，使得这两种脆性因子不能很好地解释岩石脆性由砂岩、砂质泥岩到泥岩逐渐降低的变化规律，而图5c所示的新脆性因子能够比较好地解释三者之间脆性的差异。需要说明的是，公式（8）中的脆性系数决定于起标定作用的弹性参数脆性因子，不同的弹性参数脆性因子对于某些矿物的相对大小关系不同，例如表1所给出的数值显示，公式（1）—（4）所确定的黏土与干酪根的脆性值相对大小关系不同，如果能够在实验室测得不同纯矿物的脆性系数，对于该矿物脆性因子将是一个改进。

图4 不同矿物的脆性系数

图5 3种矿物脆性因子对比图

1.3 脆性因子对比分析

图6为利用上述7个脆性因子公式对中国南方某页岩气井的计算结果。图中第5道计算TOC值由Δ logR方法[9-10]得到，第6道为X射线衍射分析获得的矿物含量。第7道为3种矿物脆性因子的对比，可见结果差别较大，公式（6）未考虑灰岩对脆性的贡献，而公式（7）过分考虑了灰岩的贡献。综合来看，相较其他两种矿物脆性因子，新的矿物脆性因子能够较好地反映不同矿物对脆性的贡献。第8、9、10、11道分别为根据测井曲线由公式（1）—（4）所计算的弹性参数脆性因子及与新矿物脆性因子的对比。由图中第11道可见，由于来源于新的弹性参数脆性因子，新矿物脆性因子与新弹性参数脆性因子的趋势基本一致，部分井段两者不一致，其原因有两点：矿物含量（第6道）为岩心分析结果，由于岩石的非均质性、岩心归位误差等原因，导致岩心测量结果与测井曲线表征的信息有差异；矿物脆性因子是每种矿物脆性程度与矿物含量乘积的加权，脆性因子与矿物含量呈线性关系，而弹性参数脆性因子与矿物含量呈非线性关系，并且考虑了其他因素的影响，如孔隙，流体等。此外，使用矿物含量表征脆性本身具有一定缺陷：①储集层岩石由矿物、孔隙、孔隙流体组成，仅考虑矿物不能代表整体岩石的脆性；②储集层岩石矿物的分布形式，以及岩石结构均非常复杂，比如固体颗粒分布形式、胶结物及胶结程度等都会对岩石的脆性造成影响；③储集层岩石处于一定温度、压力条件下，环境不同时其脆性也不同。因此，总体而言，能够反映储集层原位条件、物质组成及结构、孔隙、流体等综合特征的弹性参数脆性因子优于矿物脆性因子。在无法得到弹性参数的情况下，可通过多矿物测井解释、全岩分析等手段，得到矿物组成数据，使用矿物脆性因子进行脆性评价。

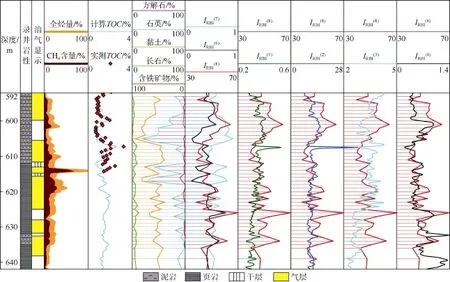
图6 中国南方某页岩气井脆性评价结果对比图（IRBI(1)，IRBI(2)，IRBI(3)，IRBI(4)，IRBI(6)，IRBI(7)和IRBI(8)分别为公式（1）、（2）、（3）、（4）、（6）、（7）、（8）计算的脆性因子）

2 岩石物理模型及脆性因子量版

上文所提出的矿物脆性因子可直接应用于测井解释，在有横波资料的情况下，弹性参数脆性因子也可以应用于测井解释，弹性参数脆性因子可直接由叠前地震资料反演所得弹性参数计算求得，而矿物脆性因子不能直接应用于地震资料。为了精确、直观地对含孔隙储集层的脆性进行评价，需要将脆性、矿物与弹性参数联系起来。本文通过岩石物理模型正演，得到反映矿物含量、孔隙度、弹性参数、脆性因子之间定量关系的岩石物理量版，以对测井、地震资料进行解释。对于含有机质的泥页岩，较为复杂的矿物、有机质、孔隙以及流体是影响其弹性性质的主要因素，所建立的岩石物理模型应该考虑这些因素。基于Voigt[11]- Reuss[12]-Hill[13]平均公式、微分等效介质理论[14]、Berryman多种复杂孔隙类型理论[15]及Biot[16]-Gassmann理论[17]，本文建立了富有机质泥页岩岩石物理模型[10]，该模型能够描述多种矿物（石英，方解石，黏土）、干酪根（有机质）、孔隙及其中的流体与弹性参数之间的关系，其中，将干酪根等效为具有一定形状的包体颗粒，其形状使用椭球体（颗粒纵横比表征形状）来描述，而将岩石中的孔隙等效为由球状孔隙、针形孔隙、硬币状裂缝混合构成。

图7为岩石物理模型的建模流程，其步骤为：①使用Voigt-Reuss-Hill平均公式计算不含孔隙的岩石基质的弹性模量（体积模量或剪切模量）MVRH：

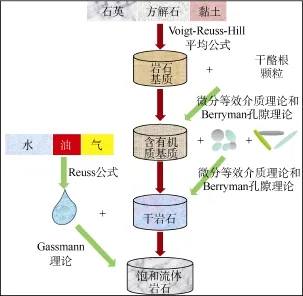
图7 富有机质泥页岩岩石物理模型建模流程图

②使用微分等效介质理论和Berryman的孔隙理论，将干酪根作为具有一定形状的包体加入岩石基质中，得到含有机质的岩石基质的体积模量和剪切模量，公式如下：

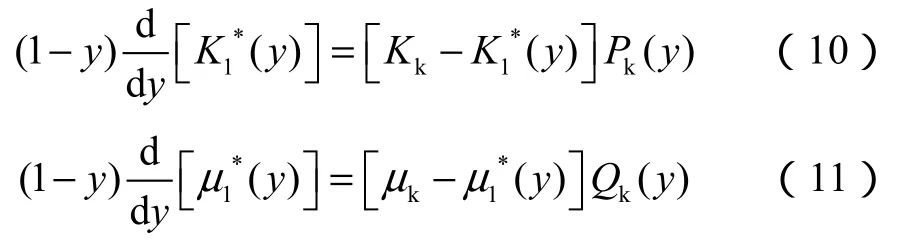
其中，K1*(0)=Km，μ1*(0)=μm。

③使用微分等效介质理论和Berryman的孔隙理论，将干孔隙加入含有机质的岩石基质中，得到含孔隙的干岩石的体积模量和剪切模量：

其中，K2*(0)=K1*，μ2*(0)=μ1*。

④使用Reuss公式得到混合流体的体积模量，并使用Gassmann方程加入干岩石中，得到饱和流体岩石的体积模量和剪切模量：

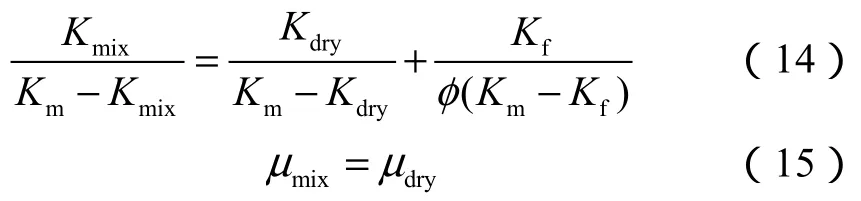
⑤使用体积模量、剪切模量、密度与速度之间的关系（公式（16）与公式（17）），计算饱和流体岩石的纵、横波速度，进而可以得到弹性模量、泊松比等其他弹性参数。

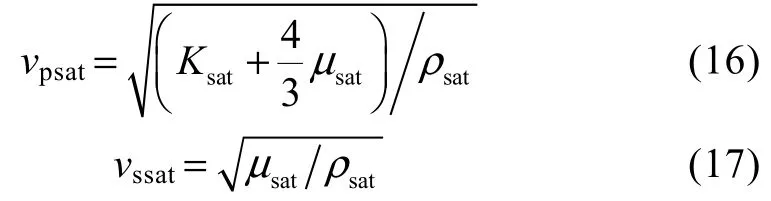
其中，ρsat=ρ0(1-φ)+ρfφ。

使用岩石物理模型制作量版过程中，使用的纯石英、方解石、黏土、干酪根、盐水、油气的弹性参数及密度如表2所示。

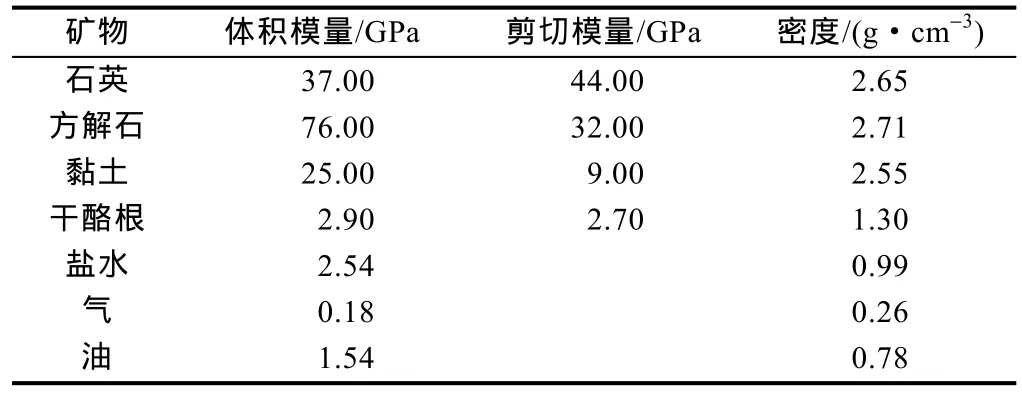
表2 部分矿物及流体弹性参数及密度[18]

建立不同矿物、孔隙度、流体的组合，使用岩石物理模型计算得到不同矿物成分、孔隙度及含流体时的速度及密度，进而得到其他弹性参数，这些数据及其变化规律代表了一定物质成分及特征的储集层的参数变化规律。图8、图9分别为新矿物脆性因子、新弹性参数脆性因子的岩石物理量版，该量版以弹性模量-泊松比参数交会图为基础，使用不同颜色表征脆性因子。图中多边形的4个端元点分别代表100%的黏土、方解石、石英及干酪根（数据见表1），浅蓝色的圆圈连线代表不同基质组成条件下孔隙度从0变化到10%（变化率为2%）的弹性参数。以石英端元点为例，在石英端元点上的浅蓝色圆圈代表纯石英，孔隙度为0，远离石英端元点的5个浅蓝色圆圈依次代表孔隙度为2%、4%、6%、8%、10%，孔隙中流体为气水比4∶1的混合流体。图8、图9的色标分别为新矿物脆性因子、新弹性参数脆性因子，从图中可以看出，弹性模量越大，泊松比越小，脆性程度越高；矿物脆性因子与弹性参数脆性因子的变化趋势相同，但是其变化率不同，这是由于矿物脆性因子是基于端元点数值的数据加权，在端元点（纯矿物）上与弹性参数脆性因子一致，而加权计算使得在混合矿物情形下变化率稳定；而弹性参数脆性因子反映储集层参数和弹性参数之间的非线性关系（岩石物理模型），其变化是非线性的。将实际测井数据投入岩石物理量版中。图中，砂岩的脆性最高，其次为砂质泥岩，泥岩的脆性最低，对于含气泥岩，由于含气使得泊松比降低，进而使得脆性增高，这与岩石物理量版反映的规律一致。从量版中可以总结出如下规律：含气泥岩的弹性模量在32 GPa之下，泊松比小于0.25，在各种岩性中其脆性中等—低值，大部分数据点矿物脆性因子为0.3～0.7，弹性参数脆性因子为5～10。

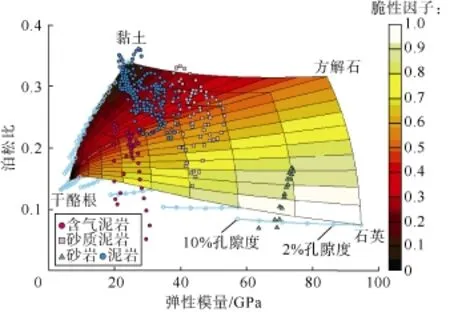
图8 新矿物脆性因子岩石物理量版（浅蓝色的圆圈连线代表不同基质组成条件下孔隙度从0变化到10%（变化率为2%）的弹性参数）

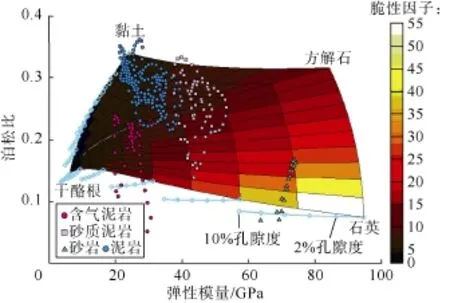
图9 新弹性参数脆性因子岩石物理量版（浅蓝色的圆圈连线代表不同基质组成条件下孔隙度从0变化到10%（变化率为2%）的弹性参数）

根据岩石物理模型，对不同矿物中含孔隙及其中含油、气、水情况下的脆性变化进行讨论，矿物及流体的参数由表2给出。如图10所示，当矿物不同时，在含孔隙及流体时其脆性变化规律不同；石英含孔隙及其中含流体时脆性变化程度大于方解石和黏土；孔隙度增大，脆性降低；在同样的矿物及孔隙度情况下，含气岩石的脆性大于含油、水岩石。

3 优质泥页岩识别

通过叠前地震反演，得到纵、横波阻抗，进而得到弹性模量、泊松比、弹性参数脆性因子（见图11），将反演结果与井资料叠合显示（A井为直井，B井为水平井），所反演的弹性模量、泊松比及计算的新弹性参数脆性因子与井吻合较好。在此基础上，对脆性泥页岩甜点进行识别。图12是地震资料反演的弹性模量、泊松比及弹性参数脆性因子的交会图与含气脆性泥岩展布剖面。根据图8、图9量版所示含气泥岩的脆性特征对反演结果进行解释，得到优质含气脆性泥岩的空间展布（见图12b），该图以泊松比剖面进行展示，图中白色曲线为目的层顶底界；黑色区域为由图12a所示交会图中多边形所抓取的数据，即优质含气脆性泥岩，由图可见，所预测的优质含气泥岩与测井结果对应较好。

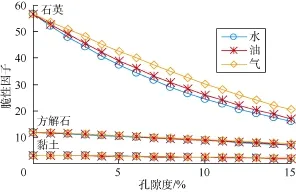
图10 新弹性参数脆性因子随孔隙度及流体变化规律图

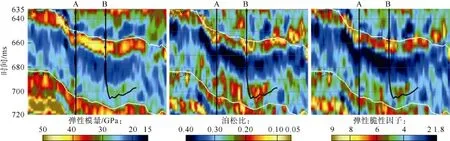
图11 叠前地震资料反演结果及计算的新弹性参数脆性因子

图12 叠前地震资料反演结果交会图及脆性含气泥岩甜点识别结果

4 结论

通过测井、地震得到的储集层弹性参数是原位条件下储集层物质组成、结构、孔隙及流体的综合响应，可以用来构建评价储集层脆性程度的脆性因子，参考前人的研究成果，本文建立了一个新的弹性参数脆性因子，相比较于其他弹性参数脆性因子，新建脆性因子敏感性较高且能够比较好地解释储集层岩石的脆性变化。

根据弹性参数脆性因子，确定了泥页岩中主要矿物的相对脆性程度（即矿物脆性系数），在此基础上构建与每种矿物脆性系数相关的新脆性因子。相较于其他矿物脆性因子，新矿物脆性因子理论优势明显且能够较好地解释储集层岩石的脆性变化。

根据富有机质泥页岩的岩石物理模型，结合所建立的脆性因子，建立矿物-弹性参数-脆性因子岩石物理量版，根据岩石物理量版可以对测井、叠前地震资料反演结果进行解释、分析。

根据富有机质泥页岩的岩石物理模型及所建立的脆性因子，对不同矿物含孔隙及流体时的脆性变化进行研究，认为不同矿物情况下，包含孔隙及流体时岩石的脆性变化规律不同，石英含孔隙及流体时脆性变化程度大于方解石和黏土；孔隙度增大，脆性降低；在同样的矿物及孔隙度情况下，含气岩石的脆性大于含油、水岩石的脆性。

根据岩石物理量版对测井资料分析所得到的规律，本文所研究实例中含气脆性泥岩的弹性模量小于32 GPa，泊松比小于0.25，而脆性中等偏低，矿物脆性因子为0.3～0.7，弹性参数脆性因子为5～10。对叠前地震资料反演结果进行分析，预测得到优质含气脆性泥岩的空间展布，所预测的优质含气泥岩与测井结果对应较好。

符号注释：

IRBI——相对脆性因子，无量纲；E——弹性模量，GPa；υ——泊松比，无量纲；λ——第1拉梅系数，GPa；μ——剪切模量，GPa；S——弹性参数脆性因子的区分能力，即敏感性，无量纲；A1，A2——采用相同方法计算的硅质页岩和钙质页岩脆性因子，无量纲；fQ，fCa，fCl，fK——岩石中石英、碳酸盐、黏土及干酪根的体积分数，%；ai——不同矿物脆性系数，无量纲；fi——不同矿物含量，可由全岩分析或者测井多矿物解释获得，%；n——矿物种类；Mi——第i种矿物的弹性模量，可以是体积模量或剪切模量，GPa；MV，MR——Voigt平均模量和Reuss平均模量，GPa；y——干酪根含量，%；K1*(y)，μ1*(y)——含有机质的岩石基质的体积模量和剪切模量，GPa；Kk，μk——干酪根的体积模量和剪切模量，GPa；Pk，Qk——表征干酪根形状的形状因子[15]，无量纲；Km，μm——岩石基质的体积模量和剪切模量，GPa；φ——孔隙度，%；K2*(φ)，μ2*(φ)——含有孔隙的干岩石的体积模量和剪切模量，GPa；Kpf，μpf——孔隙充填物的体积模量和剪切模量，GPa；Ppf，Qpf——表征孔隙形状的形状因子[15]，无量纲；Kmix，μmix——混合流体的体积模量和剪切模量，GPa；Kf——流体的体积模量和剪切模量，GPa；Kdry，μdry——干岩石的体积模量和剪切模量，GPa；vpsat，vssat——饱和流体岩石的纵、横波速度，m/s；Ksat，μsat——饱和流体岩石的体积模量和剪切模量，GPa；ρsat——饱和流体岩石的密度，g/cm3；ρ0，ρf——岩石基质、孔隙流体的密度，g/cm3。

[1] Hucka V,Das B.Brittleness determination of rocks by different methods[J].Mechanics and Mining Sciences and Geomechanics Abstracts,1974,11(10): 389-392.

[2] Kahraman S.A brittleness index to estimate the sawability of carbonate rocks[R].Brno,Czech Republic: The International Symposium EUROCK 2005,2005.

[3] Andrissi G,Loi G,Trois P,et al.Combining mechanochemistry and innovative diamond wire saws for improving productivity in granite quarries[J].Mining Engineering,2005,57(5): 46-52.

[4] Mavko G.Rock physics of shale[R].Stanford,USA: Stanford Rock Physics Laboratory,2010.

[5] Altindag R.The evaluation of rock brittleness concept on rotary blast hole drills[J].The Journal of the South African Institute of Mining and Metallurgy,2002,102: 61-66.

[6] Rickman R,Mullen M,Petre E,et al.A practical use of shale petrophysics for stimulation design optimization: All shale plays are not clones of the Barnett Shale[R].SPE 115258,2008.

[7] Guo Z,Chapman M,Li X.A shale rock physics model and its application in the prediction of brittleness index,mineralogy,and porosity of the Barnett Shale[M]//SEG technical program expanded abstracts 2012.Tulsa: Society of Exploration Geophysicists,2012: 1-5.

[8] Liu Z,Sun S,Sun Y,et al.Formation evaluation and rock physics analysis for shale gas reservoir: A case study from China south[M]//EAGE Annual Meeting Expanded Abstracts.Houten,The Netherlands: EAGE,2013.

[9] Passey Q,Creaneys S,Kulla J,et al.A practical model for organic richness from porosity and resistivity log[J].AAPG Bulletin,1990,74(12): 1777-1794.

[10] Dong N,Liu Z,Sun Z,et al.Evaluation and improvement of velocity-prediction models and its application in in-situ stress estimation for shale gas reservoir[M]//EAGE Annual Meeting Expanded Abstracts.Houten,The Netherlands: EAGE,2013.

[11] Voigt W.Crystal physics[M].Leipzig: Teubner,1928: 1-20.

[12] Reuss A.Stresses constant in composite,rule of mixtures for compliance components[J].Journal of Applied Mathematics and Mechanics,1929,9(1): 49-58.

[13] Hill R.The elastic behaviour of crystalline aggregate[J].Journal of Process Physical Society,1952,A65(5): 349-354.

[14] Berryman J.Single-scattering approximations for coefficients in Biot’s equations of poroelasticity[J].Journal of the Acoustical Society of America,1992,91(2): 551-571.

[15] Berryman J.Mixture theories for rock properties[C]//Ahrens T J.A handbook of physical constants.Houston: America Geophysical Union,1995: 205-228.

[16] Biot M.Theory of propagation of elastic waves in a fluid saturated porous solid[J].The Journal of the Acoustical Society of America,1956,28(2): 168-191.

[17] Gassmann F.Elastic waves through a packing of spheres[J].Geophysics,1951,16(4): 673-685.

[18] 李颖微.基于岩石物理分析的复杂碳酸盐岩储层流体识别研究[D].北京: 中国石油大学,2012.Li Yingwei.Fluid identification in complex carbonate reservoir based on rock physics analysis[D].Beijing: China University of Petroleum,2012.

（编辑 黄昌武 绘图 刘方方）

New brittleness indexes and their application in shale/clay gas reservoir prediction

Liu Zhishui1,2,Sun Zandong1,2
(1.Laboratory for Integration of Geology and Geophysics,China University of Petroleum (Beijing),Beijing 102249,China;2.State Key Laboratory for Petroleum Resources and Prospecting,China University of Petroleum (Beijing),Beijing 102249,China)

Aiming at the disadvantages of the brittleness index commonly used in oil/gas exploration,this article proposed two new brittleness indexes (elastic brittleness and mineral brittleness) in order to predict brittle shale distribution accurately: the former index,based on elastic parameters (Young’s modulus and Poisson’s ratio),characterizes the original physical properties of reservoirs,the other takes the volume content of minerals in the shale and brittle factor of each kind of mineral into consideration.The two proposed brittleness indexes have theoretical advantages and can explain the brittleness of reservoir rocks from logging and prestack seismic inversion reasonably.According to the rock physics model of organic-enriched shale,a rock physics template for mineral-elastic parameter-brittle factor was established to find out the elastic parameter features of high quality brittle shale from logging data.The spatial distribution of high-quality gas-bearing brittle shale was predicted utilizing pre-stacked seismic inversion results,and the predicted results match well with the well-logging data.

relative-brittleness index;mineral brittleness;elastic brittleness;rock physics template;shale gas

国家重点基础研究发展规划（973）项目（2011CB201103）；国家油气重大专项（2011ZX05004003）

TE122.1

A

1000-0747(2015)01-0117-08

10.11698/PED.2015.01.16

刘致水（1988-），男，甘肃庆阳人，中国石油大学（北京）地质地球物理综合研究中心在读博士研究生，主要从事地震岩石物理、叠前反演及页岩气地震勘探技术研究。地址：北京市昌平区府学路18号，中国石油大学（北京）地质地球物理综合研究中心，邮政编码：102249。E-mail：zhishuiliu@yeah.net

联系作者：孙赞东（1961-），男，湖北黄冈人，博士，中国石油大学（北京）特聘教授，主要从事岩石物理、保幅处理、叠前反演相结合的弹性一体化储集层预测研究。地址：北京市昌平区府学路18号，中国石油大学（北京）地质地球物理综合研究中心，邮政编码：102249。E-mail：szd@cup.edu.cn

2014-05-12

2014-11-05