流速仪检定系统中数据处理方法的研究

金福一

（辽宁省水文局，辽宁 沈阳 110003）

流速仪检定系统中数据处理方法的研究

金福一

（辽宁省水文局，辽宁 沈阳 110003）

从转子流速仪检定原理入手导出流速仪的检定公式，对流速仪采集数据的精度及其误差问题进行讨论。由于观测结果均是一些离散点，存在误差，针对流速仪检定系统数据采集低速段和中高速段精确度低的问题，通过比较各种拟合方法，采用最小二乘法对数据进行处理。通过 LabVIEW 软件编写一个数据采集的程序，并对一组流速仪检定的实验数据进行拟合，证明采用分段最小二乘法拟合流速仪鉴定曲线的正确性和可行性。

转子式流速仪；最小二乘法；回归方程；LabVIEW

0 引言

转子式流速仪是专用于明渠水流速度测量的仪器，它广泛地应用于水文水资源部门，电力、地质、环保等部门亦有使用。为了保证测量的准确性，流速仪在出厂前或使用了一段时间（一般为1 年）之后需要对其进行检查鉴定，以确定仪器转子的转数与水流速度之间的关系，供水文技术工作者测速时查读。

流速仪的检定采用直线明槽静水检定法：在横断面均匀一致的直线静水槽中，在轨道上行驶的检定车以规定的若干个稳定速度牵引流速仪，使固定安装在测杆上的流速仪在静水中进行匀速直线运动，测定在检定车速下一系列流速仪转子的转速，而检定车速和转子转速均为离散数据，通过对这2 组离散数据点进行曲线拟合，建立流速仪直线运动方程可得到检定/校准结果，即流速仪检定方程[1]。

在广泛了解国内外流速仪检定系统的标准和设计后，根据设计要求，采用工控机作为流速仪检定系统的控制核心，控制整个系统的工作。直流调速器负责给检定车上的直流电机提供电源，并控制直流电机的运行，使检定车能在铁轨上按照指定的速度行驶。流速仪挂在检定车下方，由数据采集模块对流速仪进行转率采集，采集模块将采集的数据传输给 PLC，再由 PLC 的无线通信模块将数据发送至工控机，然而由工控机采集的数据点是一系列离散的数据点，需要对离散的数据点进一步处理，拟合得到相应的回归曲线[2]。大量实验数据表明，流速仪在中、高速范围内使用时，转子转速与水流速呈近似线性关系，而流速仪在低速段使用时，转速与流速呈非线性关系[3]。针对如何绘制流速仪曲线，提出最小二乘法数据拟合的方案。

1 曲线拟合的常用方法

常用的曲线拟合方法主要分为 2 大类：1）插值拟合方法；2）最佳均方逼近的曲线拟合方法。

插值拟合方法的核心就是构造 1 个插值函数，使得插值函数的曲线经过测试点。常用的插值方法有：拉格朗日、牛顿、分段、三次样条等插值多项式。插值方法的曲线拟合都是基于 1 点建立起来的，即插值曲线经过测试点。然而实际应用中采集上来的测试点往往由于各种原因，与理论值相比有一定的误差，因此需要 1 种曲线拟合方法，使得拟合曲线能够根据全局测试点的分布，以某种最优的方式进行逼近，拟合曲线并不需要经过每个测试点，这是最佳均方逼近的拟合方法的思想。其中，最常用的方法是最小二乘法。

2 最小二乘法的原理

最小二乘法是根据最小二乘准则，利用样本数据估计回归方程的一种方法。其拟合的基本原理是假设 1 组数据点服从 1 个多项式，以多项式的计算值与实验实际值的残差平方和最小为原则，定出多项式的各项系数。然后，用多项式的计算值代替实验值，以达到数据平滑的目的。这种方法可根据实际情况，选用不同的多项式，或改变数据组中数据点的个数，从而达到不同的效果，其数学解释如下：

由观察或测试可得到 y (x) 的一组离散数据，如表1 所示。

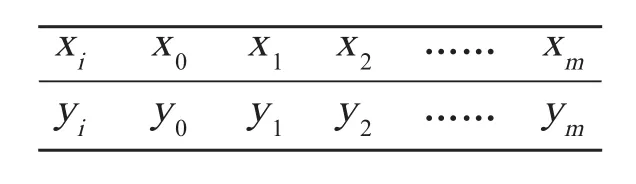
表1 最小二乘法离散数据点

与数据的背景资料规律相适应的解析表达式为[4]

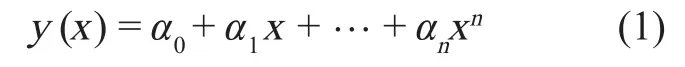
式中，α0，α1，…，αn是未知参数。由式（1）可知，最小二乘法在进行多项式拟合时，又可分为线性拟合（最高次数为 1 次）和非线性拟合（最高次数 ≥ 2 次）。

2.1 最小二乘法的线性拟合

最小二乘法的线性拟合就是将一组符合 y=α+bx 关系的测量数据，用计算的方法求出最佳的 α和 b。

设直线方程的表达式为

根据测量数据求出最佳的 α 和 b，对满足线性关系的一组等精度测量数据（xi，yi），假定自变量 xi的误差可以忽略，则在同一 xi下，测量点 yi和直线上的点 α+bxi的偏差 di如下：

显然当所有的测量点都在直线上（即 d1=d2=…=dn=0 时），所求得的 α 和 b 为最理想的。但实际所得数值，测量点不可能都在直线上，因此应使偏差 di的平方和 D 最小，即令取最小值。

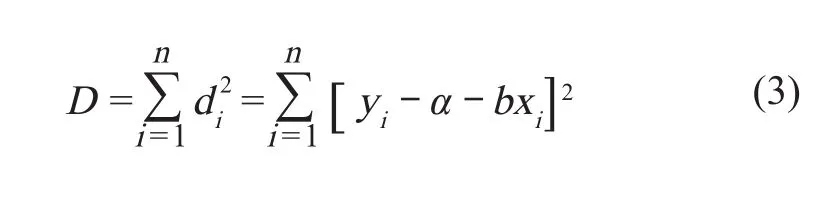
线性模型的曲线拟合问题可化为下面线性方程组的求解，通过 D 对 α 和 b 求一阶偏导数，并令其等于零，即

将 α，b 值带入线性方程 y=α+bx，即得到回归直线方程。

2.2 最小二乘法的非线性拟合

对于给定的数据点（xi，yi），1 ≤ i ≤ n 可用下面的 n 阶多项式进行拟合，即

为使拟合出的近似曲线能尽量反映所给数据的变化趋势，要求在所有数据点上残差 |δ|=|ƒ(xi)-yi|都较小。为达到上述目标，令上述偏差的平方和最小，即

确定上述多项式的过程也就是确定 ƒ (x) 中的系数 αk，0 ≤ k ≤ n 的过程，根据最小二乘原则，则偏差平方和应该是这些系数的函数 S，即

为使式（7）取值最小，则其关于 αk，0 ≤ k ≤ n的一阶导数应该为 0，写成矩阵形式为

3 最小二乘法在流速仪曲线拟合中的应用

为更精准的绘制出流速仪的ν～n 曲线，需要分别对流速仪的低速及中高速部分建立适合的数学模型。在建立数学模型时，最常用的数据处理方法基于最小二乘法。流速仪特性曲线ν～n 如图 1 所示。

图1 流速仪检定曲线

利用 LS25-1 型流速仪检定时的实验数据，基于最小二乘法拟合理论及工程上的实践经验，对流速仪特性曲线建立数学模型，运用 LabVIEW 上位机软件对系统采集到的数据进行最小二乘法的拟合验证分析，并生成打印报表[5]。LS25-1 型流速仪检定时的实验数据如表2 所示。

表2 LS25-1 型流速仪检定时的实验数据

分别对 LS25-1 流速仪的低、中高速段进行拟合，通过 LabVIEW 软件可生成如图 2，3 所示的拟合曲线及数据。

此 LS25-1 流速仪的拟合方程为

根据流速仪低、中及高速曲线的实测样本值，计算各测点绝对和相对误差及误差的总和[6]，结果如表3，4 所示。

图2 LS25-1 流速仪的中高速段曲线拟合

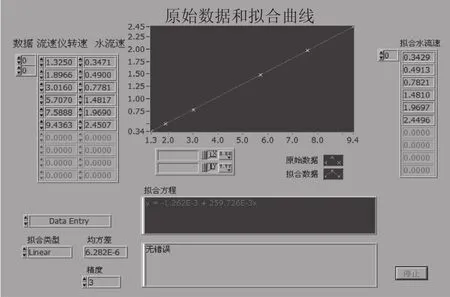
图3 LS25-1 流速仪的低速段曲线拟合

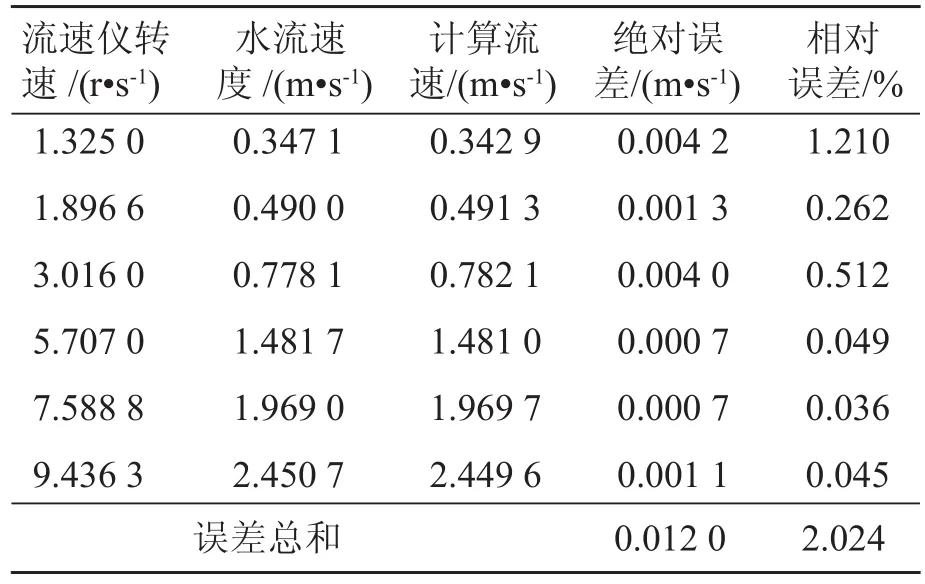
表3 LS25-1 流速仪中高速实测数据与理论数据误差分析

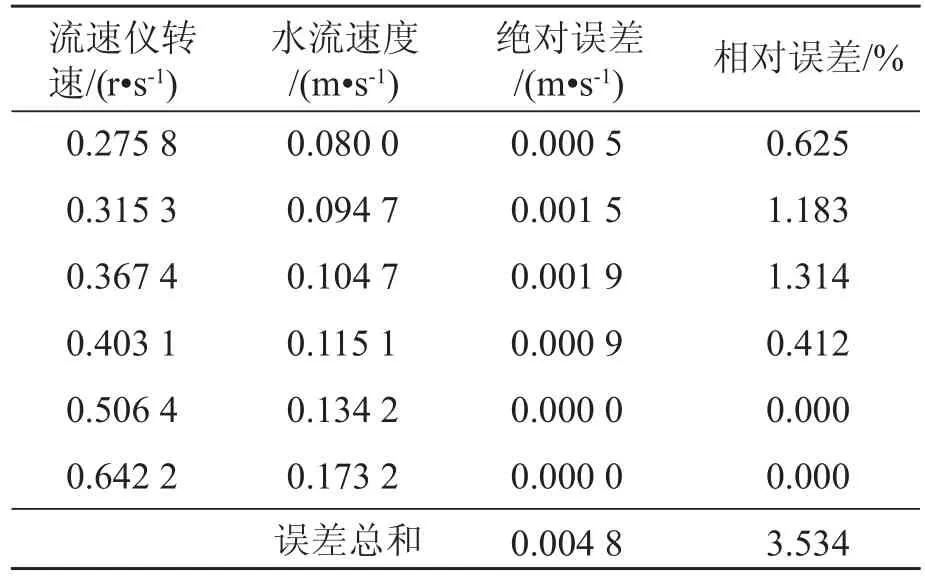
表4 LS25-1 流速仪低速实测数据与理论数据误差分析

经过计算得到，LS25-1型流速仪的测点运用上文所述的数据拟合方法进行拟合时，全线测点的绝对误差总和为 0.016 8，全线测点的相对误差总和为5.558%，均方差 m=1.125×10-6。按照标准要求，各种流速仪检定公式直线部分的全线相对均方差 m 值不大于 1.8%[7]，因此所建数学模型拟合精度较为良好，具有合理通用性，同时验证了最小二乘法进行数据拟合时有较高的精度。

4 结论

本文对流速仪检定时所采集数据的处理方法进行研究分析，结合流速仪的曲线特性及最小二乘法的原理，建立符合流速仪曲线特性的数学模型，采用一种适合流速仪低速、中高速曲线拟合的方法，即流速仪在低速段采用多项式最小二乘法的三阶拟合，中高速段采用最小二乘法的线性拟合。还通过实例验证了所建流速仪模型及选用的曲线拟合方法的精度与通用性，运用 LabVIEW 软件编程，完成系统的软件实现。

[1] 姚永熙. 国内外转子式流速仪检定方法分析[J]. 水利信息化，2012 (3): 1-5.

[2] 于彭. 流速仪自动检定系统的研究与设计[D]. 沈阳：东北大学，2003: 7-15.

[3] 姚永熙，李刚，张元义，等. GB/T 21699-2008 直线明槽中的转子式流速仪检定/校准方法[S]. 北京：中国标准出版社，2008: 6-9.

[4] 张石娃，杜军. 最小二乘法在转子流速仪检定中的应用探讨[J]. 气象水文海洋仪器，2003 (4): 28-32.

[5] 张军峰，王燕燕. 基于 LabVIEW 的曲线拟合技术的实现[J]. 仪器仪表用户，2007 (2): 49-52.

[6] 范允征，林路. 线性回归模型的深度加权最小二乘估计和拟合检验[J]. 南京师大学报：自然科学版，2008 (3): 40-43.

[7] 姚永熙，王志毅，李刚. GB/T 11826-2002 转子式流速仪[S]. 北京：中国标准出版社，2002: 3.

Study of Data Processing Method in Current Meter Verification System

JIN Fuyi
(Hydrologic Bureau of Liaoning Province, Shenyang 110003, China)

This paper exports a current meter calibration equation from the rotor current meter verification principle. The accuracy and error of data collected by velocity meter are discussed. In view of the lower accuracy of the current meter calibration system data acquisition at the low speed and high speed section, by comparing all kinds of fitting methods, it uses the least squares method for data processing. Finally, it writes a LabVIEW data acquisition software program. And a set of experimental data are fitted to prove the correctness and the feasibility by using segmented current meter identification least squares fit curve.

rotor current meter; the least squares method; regression equation; LabVIEW

P335

A

1674-9405(2015)02-0055-04

2015-01-07

金福一（1970－），男，辽宁沈阳人，高级工程师，从事水文研究工作。