基于 EEMD-ARI 的绕坝渗流量预警模型研究

杨红秀

（山西省汾河水库管理局，山西 太原 030006）

基于 EEMD-ARI 的绕坝渗流量预警模型研究

杨红秀

（山西省汾河水库管理局，山西 太原 030006）

为提高渗流量预报精度，以山西某水库古河床坝体绕渗流量为研究对象，首先基于 MATLAB 平台对其分别进行经验和集合经验模态分解，得到若干阶固有模态函数与 1 阶趋势分量，然后对各阶固有模态函数进行时序分析，建立求和自回归模型。最后通过拟合与预报精度 2 项指标对建立的 EMD-ARI 和 EEMD-ARI 模型进行比较分析。结果表明 EEMD-ARI 模型的预报精度明显高于 EMD-ARI 模型，可为大坝绕坝渗流耦合模型的构建及安全运行提供技术支持。

EMD 分解；EEMD 分解；时间序列分析；绕坝渗流预测；耦合模型

0 引言

水库蓄水后，在水位压差作用下，水会沿着坝体结合面、两岸坝端或山体岸坡中存在的颗粒孔隙、透水层、软弱夹层等渗漏通道渗往下游，形成绕坝渗漏[1]。绕坝渗漏会抬高浸润线、降低地基承载力与工程效益，当渗流量、渗透坡降等超过允许值时，大坝会发生滑坡、坍塌、接触冲刷等安全事故[2]，因此，需对大坝进行绕坝渗流监测。通过分析绕渗监测数据构建恰当模型了解大坝的绕渗演变规律，并对大坝异常情况的发生及未来运行性状做出预测。

绕坝渗流受库水位、降雨量、地质条件等因素的影响，因各因素的信号频率不同及噪声的加入，使渗流量时间序列体现出复杂的非线性、非平稳特征，因此需联合运用多种理论分析方法建立耦合模型取代单一模型对其进行预测研究。EMD（Empirical Mode Decomposition）在平稳化数据，提取出数据高、低频成分的同时可秉留原数据的属性。目前，EMD 与多种理论分析方法相结合，建立了 EMD-RVM，EMD-AC，EMD-LS_SVM 等耦合模型进行预测。EEMD（Ensemble Empirical Mode Decomposition）较 EMD 能有效地消除混频，提取出更多尺度的周期成分。利用 EMD 秉留原数据属性的特点，EEMD 消除混频、平稳化数据的特点，结合时间序列 ARI 模型具有预测精度高、先进统计性的优势，对山西某水库古河床坝体绕渗数据建立了EMD-ARI，EEMD-ARI 绕渗预警耦合模型，并对2 个模型的预报结果进行比较，以期为大坝安全运行监控及模型构建提供参考。

1 基本理论

1.1 EMD—经验模态分解法

EMD[3-4]能对信号进行自适应分解，理论上可应用于任何类型的信号分解，特别适用于分析非线性非平稳信号序列。它可将原时间序列分解为若干不同频的固有模态函数（Intrinsic Mode Function，IMF）和一阶趋势项，分解步骤如下：

1）对原序列 x (t) 的全部极大值点进行 3 次样条函数法插值，得各时刻上、下包络线值 xmax(t)，xmin(t) 及包络线均值 m (t)。

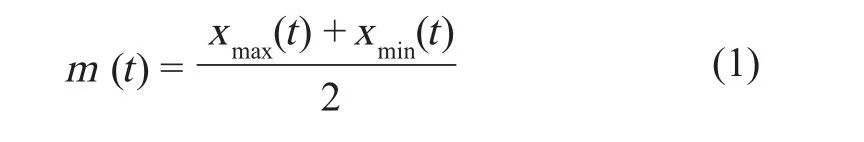
2）求类距平值函数 h (t)。

判断 h (t) 是否为固有模态函数，判断依据为：a.h (t) 函数的极值点与跨零点个数相等或仅相差 1；b. m (t) 恒等于零。满足 a，b 则 h (t) 为固有模态函数；否则将 h (t) 作为原始序列重复步骤 1）和 2），直至满足 a，b 为止。得到一阶固有模态函数 I1(t) 及剩余值序列

3）以 r1(t) 为新序列，重复以上步骤，直至分解出所有阶 IMF 分量及一阶趋势项 r (t)。

1.2 EEMD—集合经验模态分解法

EEMD[4-5]可将原序列中表征不同尺度的周期成分与趋势成分逐步分解出来，并能通过白噪声的不断加入消除模态混叠现象，分解方法为

1）在原序列 x (t) 中加入白噪声 ni(t)，得新序列

式中，白噪声 ni(t) 的统计特征为零均值，且标准差为 x (t) 标准差的 0.1～0.4 倍。

2）新序列 xi(t) 经 EMD 分解得固有模态函数ci(t) 与余项 ri(t)，步骤 1）和 2）重复 N 次，对 cij取均值得 EEMD 分解结果：固有模态函数 ，余项 r (t)，且满足：

1.3 ARI (p, d) —求和自回归模型

ARI[6-7](p, d) 模型是 d 次差分运算与 AR (p) 模型的组合，表达式为

式中：Xt为原序列；φ1，φ2，… ，φp为自回归系数；p 为自回归模型阶数；B 为后移算子；B 的次数表示后移期数；d 为差分运算次数；Φ (B) 为自回归系数多项式；αt为零均值白噪声序列。

2 工程实例分析

2.1 工程简介

某水库为兼具防洪、发电、灌溉、供水等综合效益的大（二）型水利枢纽，其控制流域面积12 380 km2。该水库于 1980 年开始信息化工程建设，其大坝安全监测项目包括：坝体表面和内部变形与坝体渗流等观测。坝体渗流观测包括左右坝基渗流、左坝岸渗流、古河床坝体绕渗、浸润线（通过测压管水位获得）和渗水透明度监测。其中，古河床坝体绕渗流量的观测仪器为矩形堰，观测频率为每周 1 次，且观测设备完好。本文用于模型构建的数据为该水库 2011 年 1 月 3 日—2013 年 5 月 20 日的古河床坝体绕渗数据，共计 125 组；用于模型检验的数据为 2013 年 5 月 27 日—2013 年 7 月 1 日的古河床坝体绕渗数据，共计 6 组，绕渗监测部分数据如表1 所示。

表1 水库古河床坝体绕渗监测数据L/s

2.2 渗流量时间序列分解

基于 MATLAB 平台对水库古河床坝体渗流量时间序列分别进行 EMD，EEMD 分解，分解结果如图 1，2 所示。EMD 分解得 4 阶 IMF 分量与 1 阶残余分量，经 Hilbert 变换及倒数运算后求得 4 阶 IMF分量的平均周期分别为 23.3，43.0，161.8，231.8 d表明渗流量时间序列可能存在 23.3，43.0，161.8，231.8 d 这 4 个波动周期[8]；1 阶残余分量的平均周期超过了序列自身长度，可能表征一种长周期成分，但由于呈现明显的单调趋势，将其作为 Res 趋势分量进行研究，可用来反映渗流量时间序列的变化规律，其总体呈上升趋势，表明坝体绕渗流量随时间的推移增加；IMF1～IMF4 及趋势项叠加形成合成序列，合成序列即为原始序列，表明 EMD 分解具有秉留原数据属性的特点。

Wu Zhaohua 和 Huang Norden E[5]通过大量实例证明，添加幅值标准差约为 0.2 的白噪声可较好的消除模态混叠现象，因此，EEMD 分解过程中取白噪声幅值标准差 Nstd 为 0.2，EMD 分解次数 NE 为100。EEMD 分解得 6 阶 IMF 分量与 1 阶残余分量，6 阶 IMF 分量的平均周期分别为 16.0 d，33.0 d，107.0 d，213.3 d，265.7 d，1.26 a，表明渗流量时间序列可能存在上述 6 个波动周期；1 阶残余分量的平均周期超过了渗流量时间序列自身长度，同样将其作为 Res 趋势分量来研究，从图 2 可看出，趋势项单调递增，表明水库坝体绕渗流量随时间的推移增加；IMF1～IMF6 及趋势项叠加形成合成序列，合成序列与原始序列存在差异，是由于分解过程中加入的白噪声对实际的 IMF 值有影响，可通过增加 EMD分解次数加以消除。

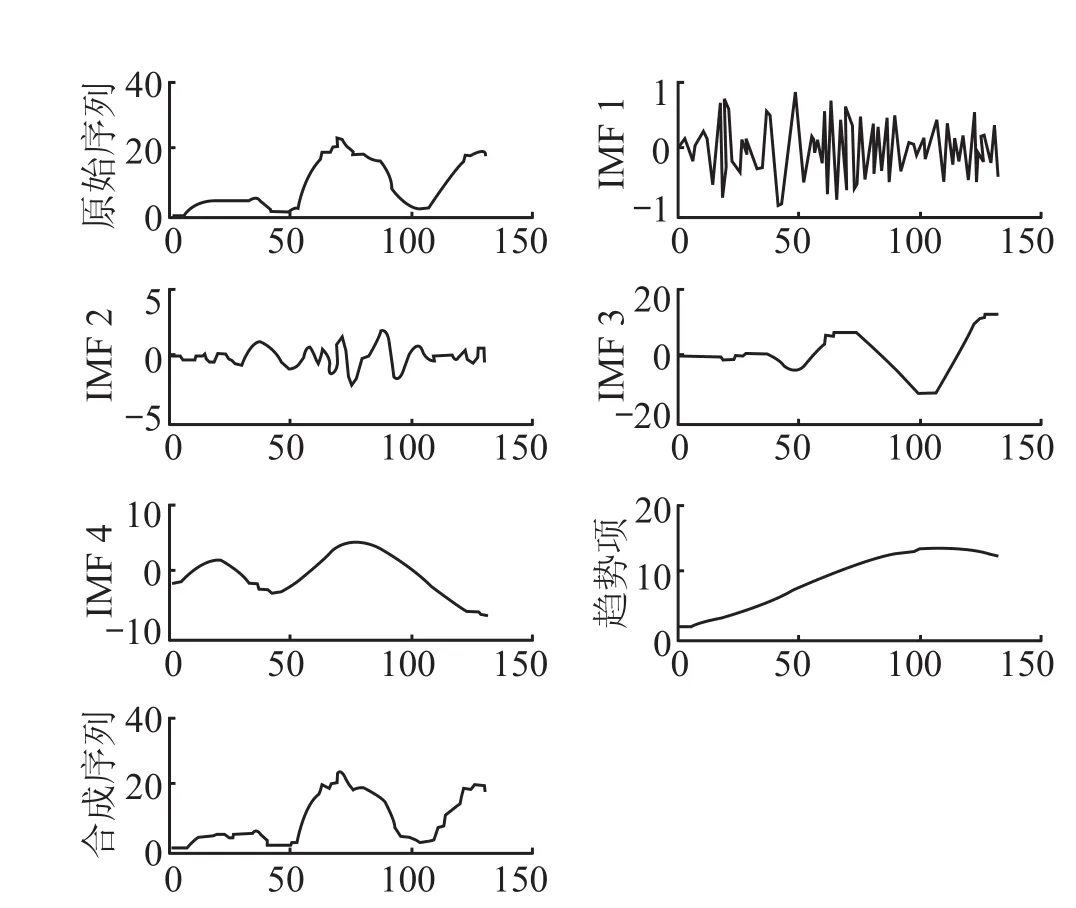
图1 渗流量时间序列 EMD 分解结果

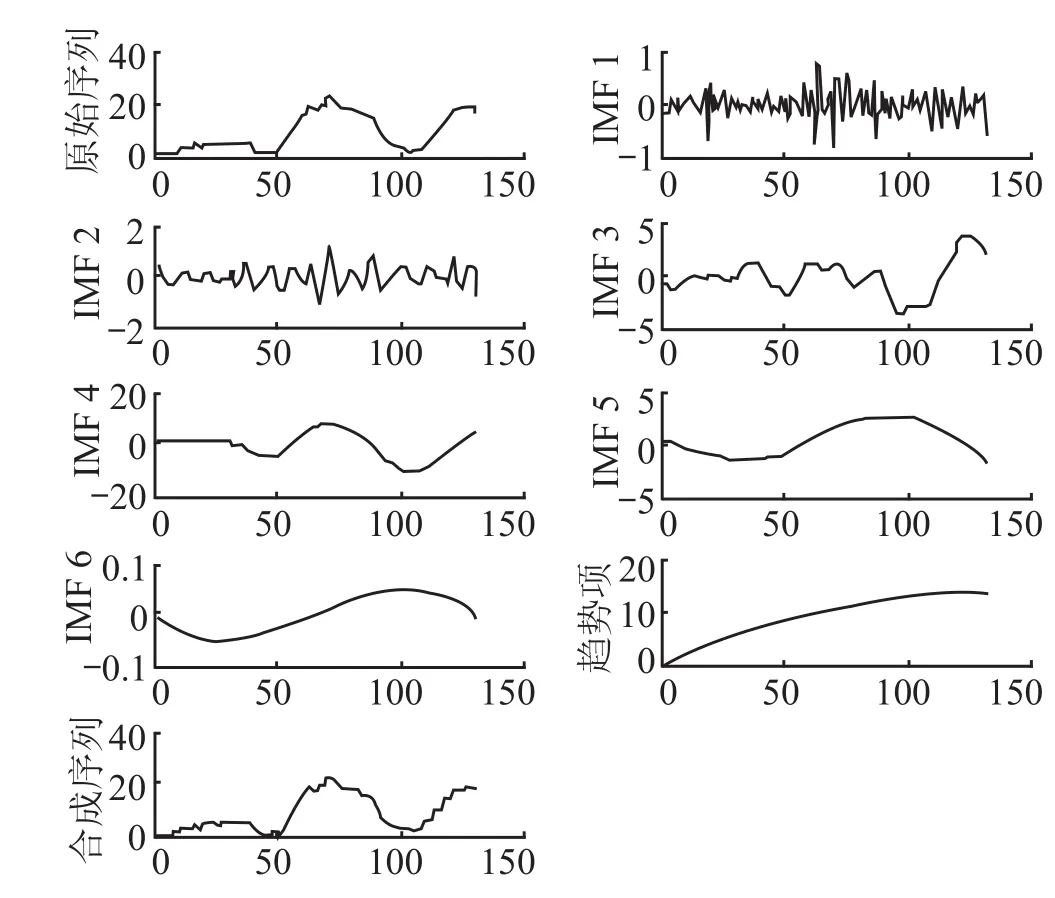
图2 渗流量时间序列 EEMD 分解结果

2.3 EMD-ARI 预警耦合模型的建立

2.3.1 AR/ARI 模型建立

对水库坝体渗流量时间序列经 EMD 分∆ARI 模型，具体步骤如下：

1）步骤 1。用 ADF 单位根检验法[9]检验 IMF1～IMF4 分量的平稳性，检验统计量为 T，检验结果如表2 所示。由表2 知，IMF1 与 IMF2 分量的 T 统计量值小于临界值-1.95，为平稳序列，IMF3 与 IMF4分量的 T 统计量值大于临界值，不平稳，对 IMF3 与IMF4 分量进行一阶差分，得∆IMF3 与∆IMF4 分量，∆ IMF3 与∆IMF4 分量经检验平稳。

表2 ADF 单位根检验结果表

2）步骤 2。检验 IMF1～IMF4 分量的纯随机性。采用 LB 检验统计量[10]对各阶 IMF 分量进行检验，检验结果如表3 所示。从表3 可看出，在延迟阶数为 6，检验水平为 0.05，临界值为 χ20.05（6）（查χ2分布表知，χ20.05（6）的值为 12.59）的情况下，各阶 IMF 分量的 LB 检验统计量值 QLB均大于临界值，且检验统计量的 P 值均小于 0.05，表明渗流量时间序列的各阶 IMF 分量均为非白噪声序列。

表3 纯随机性检验结果表

3）步骤 3。各阶 IMF 分量拟合 AR/ARI 模型 。模型阶数由 BIC 准则确定，BIC 值最小时相应模型阶数最优，其表达式如下：

根据 BIC 准则确定 IMF1～IMF4 分量的最优模型分别为 AR（1），AR（9），ARI（4，1），ARI（5，1），且通过对模型的不断调整，最终 IMF1～IMF4 分量的模型参数均通过显著性检验。

4）步骤 4。判断 IMF1～IMF4 分量的模型残差是否为白噪声。判别依据为在各延迟阶数下，若 LB检验统计量的 P（Pr ＞ChiSq）值大于检验水平，则为白噪声，否则为非白噪声。取定检验水平为 0.05，AR（1），AR（9），ARI（4，1），ARI（5，1）模型的残差均为白噪声，表明 AR/ARI 模型适合各阶 IMF分量。

2.3.2 EMD-ARI 模型结构

由于趋势项具有明显的单调性，因此用线性方程对其进行拟合，拟合表达式为

y=(1E-09) t5-(2E-07) t4-(6E-06) t3+

0.002 8 t2+0.007 6 t+2.326 4 (8)基于 SAS 平台将 4 阶固有模态函数的 AR（1），AR（9），ARI（4，1），ARI（6，1）拟合模型与 1 阶趋势项的拟合模型进行重构，建立 EMD-ARI 绕渗预警耦合模型，耦合模型共含有 30 个参数，重构数据共计 116 组，应用非线性高斯—牛顿（Gauss-Newton）法[7]进行重构后得到的模型参数最小二乘估计值如表4 所示。

表4 EMD-ARI 模型参数重构结果表

2.4 EEMD-ARI 绕渗预警耦合模型的建立

水库坝体渗流量时间序列经 EEMD 分解得 6 阶IMF 分量，对 6 阶 IMF 分量进行时间序列分析，建立相应 AR/ARI 模型，分析步骤同 2.3.1 所述，最终确定 IMF1～IMF6 分量的最优模型分别为 AR（4），AR（7），ARI（4，1），ARI（6，1），ARI（6，2），ARI（6，1）。

EEMD 分解所得趋势项单调递增，对其进行线性方程拟合，拟合结果为

基于 SAS 平台将 6 阶固有模态函数的 AR（4），AR（7），ARI（4，1），ARI（6，1），ARI（6，2），ARI（6，1）拟合模型与 1 阶趋势项的拟合模型进行重构，建立 EEMD-ARI 绕渗预警耦合模型，耦合模型共含有 46 个参数，重构数据共计 117 组，应用非线性高斯—牛顿（Gauss-Newton）法进行重构，得到的模型参数最小二乘估计值如表5 所示。

水库 EEMD-ARI 绕渗预警耦合模型的结构为

表5 EEMD-ARI 参数重构结果表

3 预警耦合模型预报结果分析

1）EEMD-ARI 模型与 EMD-ARI 模型的拟合结果分别如图 3，4 所示，从图 3，4 可看出 2 个模型的预报值与实测值的吻合度均较高、拟合效果均较好。

2）EMD-ARI 与 EEMD-ARI 模型的预报结果如表6 所示，由表6 知：a. EEMD-ARI 模型的预报值与实测值的相对误差 E 较 EMD-ARI 模型偏小；b. EEMD-ARI 模型第 6 步预测的相对误差值为 6.54%，小于 EMD-ARI 模型的 10.78%；c. E ＜ 10 时 EEMDARI 模型的预报合格率为 100%，高于 EMD-ARI 模型的 83%，E ＜ 15 与 E ＜ 20 时 2 个模型的预报合格率均为 100%，满足相对误差 E ＜ 20% 的要求。

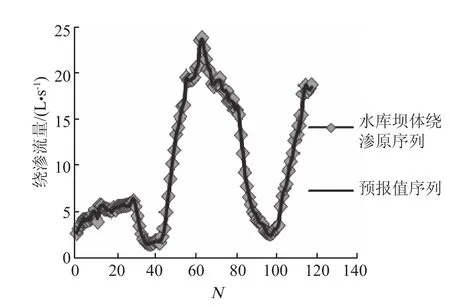
图3 EEMD-ARI 绕渗模型拟合图

图4 EMD-ARI 绕渗模型拟合图

4 结论

1）IMF 分量表征周期成分，水库坝体渗流量时间序列经 EMD，EEMD 分解所得的 IMF 分量阶数分别为 4 和 6，表明 EEMD 有效解决了模态混叠现象；1 阶趋势项均呈上升趋势，表明绕渗流量随时间推移增加，绕坝渗漏属于原古河槽渗漏，其渗流量随库水位的抬高加大，从多年统计资料分析，其渗漏基本稳定，无防渗措施。

2）本文 1 步预测的时间间隔为 7 d，EMD-ARI模型第 6 步预测的相对误差超过 10%，适用于进行5 步预测，即预测水库未来 35 d 以内的坝体绕渗流量，EEMD-ARI 模型第 6 步预测的误差较小，可对水库坝体绕渗流量进行 6 步甚至更多步预测。

3）EEMD-ARI 模型的预报精度高于 EMD-ARI模型，可用于坝体绕渗流量的预测，可为大坝绕渗耦合模型的构建及安全运行计算机决策支持系统的开发提供技术支持。

4）本模型从绕渗流量自身出发，对其未来演变规律进行预测，可进一步结合上下游库水位、降雨量等影响因素建立多元模型进行绕渗流量的预测。

表6 渗流模型预报误差分析表

[1] 康迎宾，李琳. 涧里水库大坝右岸坝肩绕渗稳定分析[J].人民黄河，2009, 31 (4): 109-113.

[2] 郑东健，王建. 绕坝渗流地下水位的时空分布模型研究[J].水科学进展，2005, 16 (5): 730-734.

[3] NORDEN E. HUANG, ZHENG SHEN, STEVEN R. LONG, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis [J]. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 1998, 454: 903-995.

[4] 张超，陈建军. EEMD 方法和 EMD 方法抗模态混叠对比研究[J]. 振动与冲击，2010, 29 (增刊 1): 87-90.

[5] ZHAOHUA WU, NORDEN E. HUANG. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in adaptive data analysis, 2009,(1): 1-41.

[6] 汪海波，罗莉，吴为，等. SAS 统计分析与应用从入门到精通 [M]. 2 版.北京：人民邮电出版社，2013:159-180.

[7] 高惠璇. SAS 系统 SAS/STAT 软件使用手册[M]. 北京：中国统计出版社，1997: 200-300.

[8] 赵雪花，安莉莉，袁旭琦. 基于 HHT 和 R/S 分析的黄河上游年径流序列演变模式分析[J]. 水电能源科学，2013, 31 (7): 9-12.

[9] 王燕. 应用时间序列分析[M]. 北京：中国人民大学出版社，2005: 142-210.

[10] 王振龙. 应用时间序列分析[M]. 2 版.北京：中国统计出版社，2010: 100-151.

Early Warning Model of Seepage around Dam based on EEMD-ARI Combined Method

YANG Hongxiu

(Fenhe Reservoir Management Bureau in Shanxi Province, Taiyuan 030006, China)

In order to improve the prediction accuracy of seepage around, taking a reservoir ancient riverbed dam body seepage data in Shanxi Province as the research object, it is respectively decomposed by using the Empirical Mode Decomposition(EMD) and Ensemble Empirical Mode Decomposition(EEMD) method based on the MATLAB platform. It receives several Intrinsic Mode Functions(IMF) and one trend component, conducts time series analysis with all the IMF, builds Auto Regressive Integrated(ARI) model. It compares and analyzes the fitting results and prediction precision of two coupling models. The results show that the prediction accuracy of EEMD-ARI model is significantly higher than the EMD-ARI model, which can provide technical support for the construction of the dam seepage around dam coupling model and safe operation.

empirical mode decomposition; ensemble empirical mode decomposition; time series analysis; seepage around the dam forecasting; coupling model

TV64

A

1674-9405(2015)02-0018-06

2014-08-11

杨红秀（1971－），女，山西夏县人，高级工程师，主要从事水库信息化理论方面的研究。