动态随机非参数数据包络分析法及其应用
2015-01-02汪茂泰何永芳
汪茂泰,何永芳
(1.安徽工程大学 人文学院,安徽 芜湖 241000;2.西南财经大学 工商管理学院,成都 611130)
随机非参数数据包络分析(StoNED)是Kuosmanen(2006)提出的一种效率测度的非参数前沿分析方法。该方法较好的将随机误差项与非效率项进行了有效分离,又免除了生产函数形式预设导致设定误差与效率估计相混淆的缺陷;且该方法仅依赖于DEA和SFA所建立的原有概念和原理,无需引入新的概念和工具,对于熟悉DEA和SFA的学者可以比较容易理解和掌握。因此,StoNED一经提出就得到广泛的应用和扩展。
1 动态随机非参数数据包络分析法
StoNED标准模型最早围绕截面数据开展研究,但需要对技术非效率项以及随机误差项做标准的SFA假设(非效率项和随机误差项必须分别服从截取正态分布和标准正态分布)。而面板数据有助于减少截面数据模型的参数分布的相关假设,并且可以采用纯非参数形式来估计前沿面以及非效率项。
考虑到生产技术和效率变化,我们在生产函数 f(x)的基础上引入时间变量t,把生产函数重新设定为f(x ,t),t=0,1,···,T ;同时用 ui(t)替代非效率项ui。
在StoNED标准模型中,假设合成误差的方差是独立于厂商规模的,一旦违背此假设可能会导致不同厂商之间出现异方差性。因此,我们采用乘法误差结构形式来从降低可能存在的异方差性。基于应用方便的目的,我们将StoNED模型设定为如下形式:

其中,f(xit,0)是指基期的生产函数,而函数Am(t)表示投入型技术进步。可以证明:若 f(xit,0)单调递增且Am(t)≥0 ,则 f(xit,t)也是单调递增的;若 f(xit,0)是凹的,则 f(xit,t)也是凹的。显然,方程(3)优良的特性给我们在StoNED框架下设置技术进步提供了方便:可以用非参数形式来估计基期生产函数 f(xit,0),用非参数或者参数形式来设置技术进步。更重要的是,不管如何设置Am(t)的形式,都不会影响 f(xit,t)的凹性在不同时期的一致性。
为了减少待估参数的个数,我们采用二次方程(新引入2M个未知参数)设定技术进步:

在CNLS(凹面非参数最小二乘法)框架中,使用纯非参数形式来设定效率变化是不可行的,除非强加众多的严格假设。如果没有足够的严格约束,效率变化很难与随机误差区别开。因此,我们采用半参数方法:非参数形式估计生产函数,参数方程来估计非效率项ui(t)。按照Cornwell et a(l1990)的做法,将非效率项设定为二次多项式:

若bi=ci=0,表示效率变化水平是常数;若bi≻0,ci=0,表示效率变化呈线性增长;若ci≠0,表示效率呈非线性变化。
将式(2)、(3)、(4)和式(5)相结合,得到待估计的回归方程:

为了估计基期生产函数 f(xit,0)以及参数θ、ψ、a、b、c,构建CNLS估计模型:
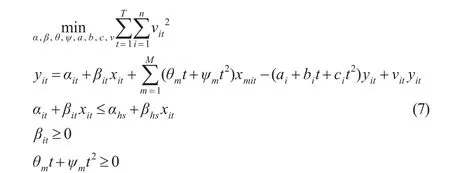
其中,目标函数是最小化误差项的L2范数。第一约束是回归方程,用切超平面αit+βitxit来表示基期生产函数f(xit,0);第二约束是用不等式对切超平面施加凹形限定;第三约束是对生产函数施加单调性限制;第四约束是技术限制。以上约束条件可以确保 f(xit,t)的单调性和凹性。
以上模型可以采用GMAS(General Algebraic Modeling System)软件进行估计。
2 数据来源与处理
本文所使用的原始数据来自中国官方公开出版的2004~2010年间服务业分行业数据。经过适当处理,这些数据构成了一个包括14个服务行业在7年里共98个观察值的面板数据。
2.1 分行业的实际产出
本文采用增加值作为度量服务业产出的指标。2004~2010年服务业分行业的增加值数据来自历年的《中国第三产业统计年鉴》和《中国统计年鉴》。《中国统计年鉴》给出了历年第三产业增加值指数(上年为基期)。由于数据的限制,除了“交通运输、仓储和邮政业”、“批发和零售业”、“住宿和餐饮业”、“金融业”以及“房地产业”直接使用各自给定的增加值指数外,其他行业均统一使用“其他”栏给定的增加值指数。将上述增加值指数换算成以2004年为基期的增加值平减指数,并对历年服务业各行业名义增加值进行折实处理,就可以得到历年服务业分行业的实际产出。
2.2 分行业的劳动投入
劳动投入虽然包括就业人数、劳动收入、劳动时间、劳动强度以及劳动质量等方面的内容,但众多学者均认为用就业人数来代替劳动投入的变动是合适的(原毅军等,2009),因此本文也采用此指标来衡量劳动投入。
《中国第三产业统计年鉴》并未公布2004年以来分行业年底就业总人数,只公布了城镇单位、私营和个体就业人数等城镇就业人数。考虑到安徽的就业结构比较接近于全国的水平,所以我们假设全国第三产业各行业乡村就业人员比例结构与安徽是一致的,从而可以根据第三产业总就业人数、城镇就业人数以及安徽省第三产业各行业乡村就业人员结构估计出全国第三产业各行业乡村就业人数,再将城镇就业人数与乡村就业人数相加就近似得到2004~2010年分行业年底就业总人数。
2.3 分行业的资本投入

《中国统计年鉴》、《中国第三产业统计年鉴》和《固定资产投资统计年鉴》给出了全行业固定资产投资指数,但未给出分行业固定资产投资指数。我们假设各行业的固定资产投资指数均等于全行业的固定资产投资指数,并调整为以2004年为基期,由此得到各行业实际固定资产投资值。结合上述估算办法,就可以得到历年各行业资本存量实际值。
3 模型及其测算
结合模型(7),本文的动态随机非参数数据包络分析模型设定为:

运用GAMS软件,可以估计出相应的参数值。
关于技术进步Am(t),结果显示资本增强型技术进步几乎为零(θK=0,ψK=0),技术进步主要体现在劳动投入上(θL=-0.064,ψL=0.064)。据测算,在7年时间里,技术进步生产函数增长了1.7倍。近年来,服务业从业人员的数量稳步上升,从业人员的质量快速提高,大量优质人才的加入使得服务业的技术进步明显。
将 f(xit,0)与Am(t)相结合来考察要素投入的边际产出(βmit+tθm+t2ψm),结果如表1所示。2004~2010年,各行业的劳动边际产出出现明显增长,而资本的边际产出出现下降或者维持不变。近年来,我国服务业的资本和劳动投入都显著增加,但相对于劳动投入,资本投入的增加更加明显(各行业固定资产投资实际年增长率在14%以上)。因此,从边际报酬递减规律来看,出现边际产出变化的分异也是一个可以预期的结果。从估计值来看,房地产行业的劳动边际产出远远高于其他行业,而居民服务和其他服务业相对最低;各行业资本的边际产出非常低,几乎接近于零。按照西方经济学理论,在完全竞争市场中,太低的边际产出意味着投资过度,而较高的边际产出意味着投资不足。虽然我国服务业市场化进程在加快,但还未形成完全竞争状态,在部分行业还存在严格的政府管制。因此,我们不能用西方经济学理论来解释这一现象。我们认为,我国资本投资并不过度,在政府管制下,有限的资本投资并没得到充分的利用,存在大量的资本浪费和闲置,太低的边际产出原因在于资本的质量以及利用不足。

表1 投入的边际产出的估计值
为清晰的比较不同年份不同行业的效率水平,我们采用标准化的形式[1/(1+ui(t))]来表示效率值,结果如表2所示。所有效率估计值均落在区间[0,1]上,效率估计值1代表最有效率,0代表最没效率。注意,这里效率估计值是全效率估计值,既包括技术效率又包括规模效率等。由表2可见:在2004~2010年间,金融业都是最有效率的;其次是房地产业,但其效率值呈逐年下降趋势;信息传输、计算机服务和软件业以及交通运输、仓储及邮政业的效率也相对较高,并且逐年稳步上升。最没效率的行业为文化、体育和娱乐业,但近年来其效率得到显著提升。为剔除行业自身内外部环境对效率估计的影响,我们考察了不同行业年平均效率变化率(相对效率可以很好的捕捉截面的异质性)。如表2所示:居民服务和其他服务业、批发和零售业以及租赁和商务服务业显示出相对较高的效率改善(年均6%以上);而住宿和餐饮业以及教育业效率改善比较温和(年均在1%左右)。整体来看,虽然我国服务业效率较低,但大部分行业均进入了快速上升阶段,只有房地产业以及水利、环境和公共设施管理业等出现效率下降现象。这也反映出我国服务业发展的阶段特征:长期以来,我国服务业进入管制较严、市场垄断程度较高,一定程度上制约了技术进步。随着服务业市场化程度的逐步提高,为应对外部竞争的加剧,各行业内部更加注重组织结构的调整和优化完善,这就为效率提升提供了巨大空间。

表2 2004~2010年相对效率水平值[1/(1+ui(t))]及其变化率 (%)
4 结论
为解释跨期生产技术和效率变化,我们介绍了动态随机非参数数据包络分析方法。
随后运用动态随机非参数数据包络分析方法,对我国服务业各行业的技术进步及其效率改善进行了测算。2004~2010年,我国服务业资本增强型技术进步几乎为零,技术进步主要体现在劳动投入上。整体来看,我国服务业效率水平较低,但大部分行业均进入了快速上升阶段。
动态随机非参数数据包络分析法为考察跨期技术变化和效率变化提供了很好的度量工具,但我们也应注意到:随机非参数数据包络分析法虽然综合了DEA和SFA的优良特质,但也保留了它们的部分局限性。在模型的设定中,众多的约束条件也带来了这种分析方法的局限性。另外,在考察技术进步时,时间跨度要足够长。本文受制于数据的可得性,我们只采用了7年的数据,技术进步的测算结果就不太准确。
[1]Kohli U.A Cross-National Product Function and The Derived Dem and for Imports and Supply of Exports[J].Canadian Journal of Economics,1982,(18).
[2]Kuosmanen T.Stochastic Nonparametric Envelopment of Data:Combining Virtue of SFA and DEA in A Unified Framework[C].MTT Discussion Paper,2006.
[3]Kuosmanen T.Stochastic Nonparametric Envelopment of Panel Data:Frontier Estimation With Fixed and Random Effects Approaches[C].MTT Discussion Paper,2010.
[4]籍艳丽,赵丽琴.一种效率测度的新方法:随机非参数数据包络分析法[J].统计与决策,2011,(5).
[5]原毅军,刘浩,白楠.中国生产性服务业全要素生产率测度——基于非参数Malmquist指数方法的研究[J].中国软科学,2009,(1).
