基于优势粗糙集构建突发事件应急通信分级模型
2015-01-02樊自甫王丽花
樊自甫,王丽花,孙 红
(重庆邮电大学 经济管理学院,重庆 400065)
0 引言
我国是一个地域广、突发事件发生频率高、事后损失较为严重的国家。通信行业作为国民经济中举足轻重的基础性行业,直接关系到突发事件发生后的通信畅通,影响国家重要信息的及时传递,进而影响突发事件保障工作的顺利进行,而应急通信的级别的确定是应急通信保障工作的重要前提,在突发事件应急通信保障中尤为重要[1]。目前我国在应急通信分类分级领域的定量研究较少,应急通信保障预案[2]中的响应等级是根据突发事件对通信基础设施造成的影响程度来划分,对不同类型、级别突发事件的主动应对能力不强,需要从通信应急保障视角对灾害事件进行性质上分类、程度上分级,建立一套新的应急通信定量分级标准。本文选择DRSA理论对突发自然灾害事件时应急通信不完备数据进行数据补齐、离散化及属性约简,并提取偏好决策规则,为优化现有应急通信保障预案体系和应急管理部门科学确定应急通信等级提供模型支撑。
1 优势粗糙集理论
优势粗糙集相关定义如下:

定义2:(优势关系)[4]令≥q为论域U上的弱偏序关系。y≥qz是指准则q上y至少和z一样好,如果对∀q∈P都有 y≥qz,则y,z在准则P∈C上的优势关系表示为yDPz。显然,优势关系具有自反性和传递性。
定义3:(上并集和下并集)[5]假设决策属性d将论域U分成有限的类集CL={Clt,t∈T},T={1,2,…,n},∀y∈U 属于且只属于其中的一个分类Clt,且假设这种分类是有序的,即对所有的 i,j∈T,如果 j>i,则 Clj中的任一对象优于(或劣于)Cli中的对象。则上并集和下并集表示为:

存在边界域问题,不一致优势粗糙集的分类质量为:

其中,ci1,…,cip表示具有优势关系的条件属性,ci(p+1),…,ciz表示没有优势关系的条件属性,tij表示属性cij的属性值。
2 基于优势粗糙集应急通信分级模型构建
2.1 分级指标体系设计
选择什么样的指标作为研究变量,对模型的准确性和可靠性有着较大影响。根据《国家突发公共事件总体应急预案》和《国家通信保障应急预案》,结合非常规突发事件下的应急通信保障特性,最终将应急通信分级指标体系分为突发事件客观因素、通信网络受损、应急通信资源、社会影响因素等4个维度,20个指标,如图1所示。

图1 应急通信保障分级指标
2.2 级别判别知识表达系统建立
假设应急通信级别判别的知识表达系统为四元组S=<U,A,V,f>,其中,U为由多值属性描述的应急通信级别论域,A为属性集合,由条件属性C和决策属性D组成,C={突发事件客观因素、通信网络受损、应急通信资源、社会影响因素},D={类别描述:1级,2级,3级,4级},V为属性对应的值域,f:U×A→V是一个应急通信分级信息函数,给每个分级对象属性赋予一个信息值。
2.3 样本选取及数据收集
本文的样本为2008~2013年之间发生并启动应急通信保障的60条突发事件案例。由于现阶段我国应急通信保障缺少专业的数据库系统[6],数据获取途径为国内通信行业网站中的新闻报道和部分国内外灾害数据库,其中,通信网络受损、应急通信资源和跨部门协调因素三类指标数据来源于工业和信息化部官网中的应急通信报道和中国信息产业网中的《自然灾害应急通信保障追踪报道》专题;突发事件客观因素和社会影响因素两类指标数据来源于国内外的相关灾害数据库,包括EM-DAT数据库、USGS地震数据库、中国海洋灾害公报和中国地震台网中心地震数据管理与服务系统等。
刘老师的父亲,曾在国民党军队中任职,从五十年代初期起,这就成为罩在他头上的阴影,对他的命运发生了深远的影响,他一直是按照自己对于国家政策的理解、认识来行事,很理性地对待。近年,确认他父亲作为国民政府远征军的一名高级军官,在中缅边境抗击日寇立下战功,他十分兴奋,写下《往事历历记心头》,把父亲生命中光荣的一页公之于世,同时,仍然冷静地表达全面认识这种问题的意向。本书把此事前前后后的情况和他在不同时期的想法真实呈现,对许多遭遇坎坷的人,是一种有益的参照。
2.4 初始应急通信分级决策表建立
样本获取后,建立初始决策表。表中的每一行代表样本突发事件,每一列代表一个属性的描述,属性分为条件属性和决策属性(自然灾害事件造成应急通信的不同级别)。其中,条件属性又分为具有偏好关系的标准和不具有偏好的常规属性。数据关系表的建立收集各灾害事件发生的各属性值而成[7]。将新闻报道和国内外灾害数据库数据进行事件匹配,构建二维决策表,形成如表1所示的不完备决策信息表(篇幅所限,只显示一部分)。
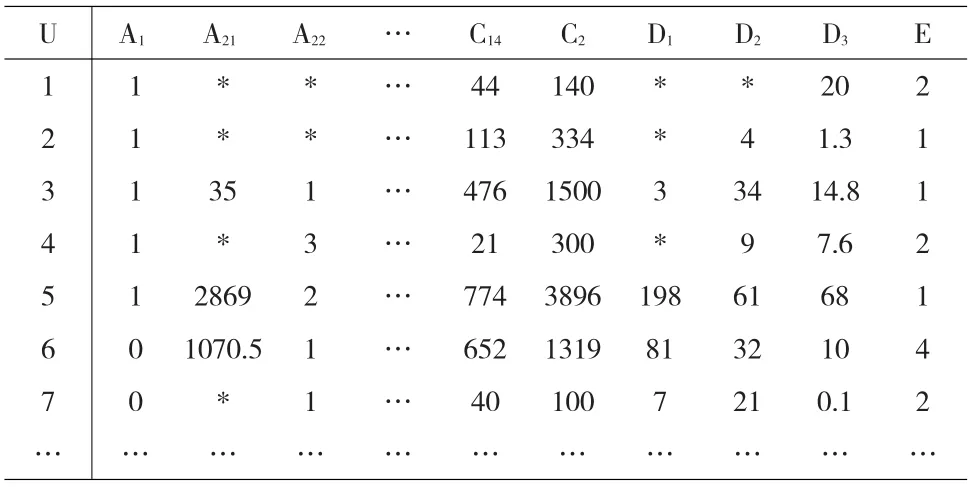
表1 原始决策信息表
2.5 数据预处理
优势粗糙集处理对象的主要是数据,而在应急通信分级指标中,存在定性指标,因此需要对定性指标进行属性赋值。如表1中的A1话务拥塞情况,话务量明显增加赋值为1,话务量平稳如赋值0。同时,对于实际数据收集中存在的数据缺失(如表1中*),应用Mean/mode法进行数据补缺,进而得到完备的数据关系表。
2.6 属性约简,规则生成
Greco等提出了DOMLEM算法[8],该算法使用迭代方法不断从训练集中提取规则,最终从学习数据集中提取出一个规则数相对较少,完备且非冗余的决策规则集。目前DOMLEM算法已被集成到JMAF(波兰科学院Slowinski院士团队开发的基于优势关系粗糙集的智能决策分析系统)中。因此,本文在使用JMAF软件进行属性约简后采用该算法提取规则,再根据支持度对规则进行选择和过滤,最终得到应急通信级别偏好规则库。
2.7 检验级别确定精度
根据规则库,对样本进行再次分级,检验该模型精度。
最后,应急管理部门或专家根据识别规则库里的偏好决策规则,确定最终的应急通信级别,整体流程如图2所示。

图2 应急通信分级模型
3 结果分析
3.1 近似质量
将原始决策信息表利用Mean/mode法进行数据补齐,得到完备二维决策表,根据优势粗糙集定义,得到各个联合类的近似质量为:,近似质量都较高,整体质量水平为96.7%。说明所选取的条件属性较为全面,能够得到比较精确的分级结果。
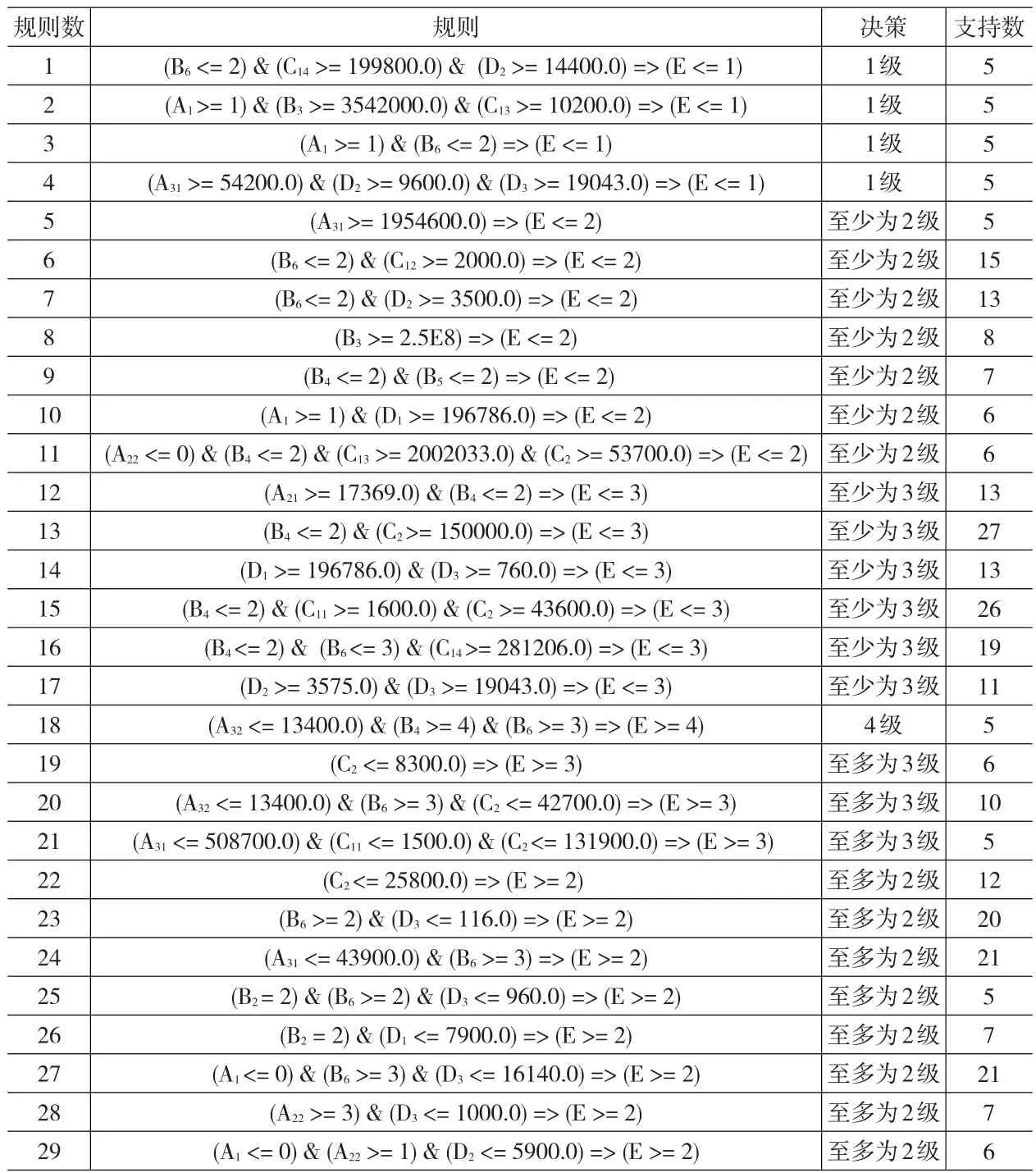
表2 规则库
3.2 属性约简结果
3.3 识别规则库形成
采用DOMLEM算法提取得到44条确定性规则,由于规则数量较多,本文选取支持度高于5的29条确定性规则形成判别规则库,如表2所示:
其中,判断级别为1级的应急通信级别规则是4条,7条规则至少为2级,8条规则为至多2级,6条规则至少为3级,3条规则至多为3级,1条规则为4级。
由以上规则可以得到以下结论:
(1)突发事件影响范围对应急通信等级的决定作用较大,例如,突发事件造成通信网络话务量急剧上升,且需要设立多个部、省联合指挥部来应对该突发事件,应急通信等级为1级(规则3);话务量没有急增,设立单一部委、省级指挥部及以下且最终的经济损失不超过1614亿元的,该级别最多设定为2级(规则27);影响范围为多个市且派遣出应急通信保障人员超过150000,则应急通信的级别至少为3级(规则13);当突发事件的影响范围仅是一个县级以内的,设立省级以下的指挥层级,且受损局点、杆路数少于13400的,仅启动4级响应(规则18)。
(2)突发事件对通信基础设施造成的损害程度对应急通信等级影响较大,例如,突发事件发生时,设立单一部委、省级指挥部及以下的,且受损局点、杆路数至多为43900处,则该应急级别设定至多为2级(规则24);当受损基站数小于等于13400个,派遣应急通信保障人员少于42700个,且设立单一部委、省级指挥部及以下的指挥部,则至多设定为3级(规则20)。
(3)应急通信资源保障对应急通信等级的设定起到一定作用,例如,如果需要设立多个部、省联合指挥部,且启用的卫星电话至少为2000部,应急通信等级至少2级(规则6);多个市受灾且启用的应急通信车至少为1600辆,派遣出应急通信保障人员超过43600辆,规定应急通信级别至少为3级(规则15)。
当发生突发事件时,应急通信管理部门或专家可以参考该模型中的规则库偏好决策规则,重点考虑11个核心影响因素,最终确立应急通信等级。上述结论同时验证了国家通信保障应急预案从不同行政范围的通信大面积中断和需提供的通信保障来划分等级的合理性,并可以根据规则中的通信基础设施损毁以及通信资源保障情况的定量数据对等级进行划分,进一步明确了国家通信保障应急预案中大面积中断的模糊概念。
3.4 模型精度检验
将60个案例使用该分级规则进行再次分级时发现,原来4个级别3被误判成级别2,1个级别2被误判成级别3,1个级别1被误判为级别2,模型整体精度为90%。说明该模型学习能力较强,能够较为准确地判别出应急通信保障级别。
4 结论
本文将优势粗糙集模型应用到应急通信分级研究中,利用优势粗糙集理论的属性约简能力,从大量的原始数据中挖掘出关键属性,采用DOMLEM算法,得出应急通信4个级别的相应判定规则。应急通信管理部门可以根据此判定规则中的级别决策范围,并结合关键属性,最后确定应急通信级别。该模型避免了应急通信级别确定的主观臆断性,且精度高达90%,具有良好的应急通信等级划分能力。
应急等级划分贯穿于整个突发事件始终,包括事情监测、预防预警、事中应急响应处置和事后分级评估等几个部分。本文提出的基于优势粗糙集的应急通信分级模型,虽然可以提高应急通信等级划分的准确性和合理性,但主要针对的是突发事件发生后的应急通信分级评估问题。未来可以就整个事件的动态级别划分问题,使用系统方法提出一套基于过程的应急通信动态分级模型。
[1]万晓榆,孙三山,卢安文.我国特大自然灾害下的应急通信管理探讨[J].重庆邮电大学学报(社会科学版),2009,(1).
[2]中华人民共和国信息产业部.国家通信保障应急预案[Z].2011.
[3]Greco S,Matarazzo B,Slowinski R.Rough Approximation of Preference Relation By Dominance Relations[J]European Journal of Operational Research,1999,(117).
[4]Greco S,Matarazzo B,Slowinski R.Rough Approximation By Dominance Relations[J].International Journal of Intelligent Systems,2002,17(2).
[5]Greco S,Matarazzo B,Slowinski R.Rough Sets Theory for Multicriteria Decision Analysis[J].European Journal of Operation Research,2001,(129).
[6]刘耀龙,许世远,王军等.国内外灾害数据信息共享现状研究[J].灾害学,2008,(3).
[7]王德鲁,宋学锋.基于战略转换的企业战略风险预警模型研究[J].管理工程学报,2010,(3).
[8]Greco S,Matarazzo B,Słowinski R,Stefanowski J.An Algorithm for Induction of Decision Rules Consistent With Dominance Principle//Proceedings of The 2nd Rough Sets and Current Trends in Computing.Berlin,Springer,2000.
