我国物价水平波动的非线性特征检验

闫树熙，吴建銮

（1.榆林学院数学与统计学院，陕西 榆林 719000；2.西安交通大学 经济与金融学院，西安 710061）

0 引言

物价水平波动是指在经济的运行过程中，整个经济体商品和劳务的价格所呈现出来的高低起伏的经济现象。物价水平作为国民经济运行的晴雨表，其波动不仅与宏观经济运行、社会安定、人民生活息息相关，而且会引起我国市场经济各个领域的变化。在宏观经济的运行过程中，货币供给量、经济增长、国际油价等诸多因素都会引起物价水平的波动，但更为重要的是物价波动本身所呈现出来的规律性，发现物价自身波动规律、分析其变动趋势对预测短期内物价走势和维持物价长期稳定具有重要的现实意义。

国内外专家学者对物价水平波动研究大致可以归纳为以下两个方面。第一个方面从物价水平与某个或某些变量的关系入手，探讨物价水平波动的决定因素或决定机制。第二个方面从物价水平自身波动入手，探究物价水平的波动规律。本文研究属于第二个方面，尝试从物价水平自身波动特征出发，探究物价水平的波动规律。以往对物价水平研究存在以下两个方面问题。一是以往研究多用CPI数据度量物价水平，衡量物价水平指标单一。本文认为，角度不同，衡量物价水平所用指标应该不同，因此衡量物价水平的指标并不唯一。如对消费者而言，物价水平应该用消费者价格指数（CPI）衡量；针对商品零售商而言，物价水平应该用商品零售价格指数（RPI）衡量；针对生产者而言，物价水平应该用生产者出厂价格指数（PSPI）和生产者购进价格指数（PBPI）衡量。二是以往研究多用线性模型（AR、MA）或本质为线性模型（ARCH、GARCH）研究物价水平波动。实际上，经济现象是非常复杂的，受诸多因素的影响，许多经济变量再其运行的过程中会呈现出非常复杂的非线性波动特征，这已被很多学者证实。线性模型很难刻画或者描述经济变量的这种复杂的非线性特征，马尔科夫区制转移模型虽然能够刻画这种非线性特征，但是其并不能给出这种非线性转移的具体形式，非线性平滑转移自回归模型（STAR）很好的解决了这个问题，其不仅能够描述这种复杂的非线性特征而且能给出非线性转移的具体形式，因此，STAR模型一经提出便备受经济学者喜爱。鉴于上述原因，本文从居民消费价格指数、商品零售价格指数等四类价格指数入手，使用STAR模型分析我国物价水平波动规律，验证其非线性特征的存在并进行建模分析。

1 STAR模型

STAR模型实质上为变系数自回归模型，最早由Granger和Terasvirta（1993）正式提出。自从其建立起，就备受计量经济学家和统计学家喜爱，是计量经济学发展的前沿内容。STAR模型的基本形式如式（1）所示：

其中，εt～iid(0，σ2)，G(St，γ，c)是平滑转移函数。G(·)的形式常用的有两种，一是logistic函数，如式（2），称为LSTAR模型；二是exponential函数，如式（3），称为ESTAR模型。

其中，γ＞0，为转移参数，描述了两种机制间的转移速度；st是转移变量，它是导致yt由一种状态平滑转移到另一种状态的变量，st可以取 yt-d、Δyt-d和时间t等；c为阈值参数，是机制转移的具体位置。STAR模型的最大特点体现在转移函数G(·)上，转移函数选取不同，其对应的STAR模型的数据生成机制不同，故其适合描述的经济现象就不会不同。

从式（2）和式（3）可以看出，对于ESTAR模型而言，当转移变量st偏离阈值参数c时是外机制，此时G(·)=1；当转移变量st在阈值参数c附近时是内机制，此时0≤G(·)＜1。对于LSTAR模型而言，当转移变量 st→-∞时是一个机制，此时G(·)=-1；当转移变量st→+∞时是一个机制，此时G(·)=1。从上述分析不难看出ESTAR模型描述的非线性平滑转移是对称的，LSTAR模型描述的非线性平滑转移是非对称的，两者的结合能够解释大多数经济现象。

目前，STAR模型的建模技术已发展的很成熟，主要要包括平稳性检验、模型设定、参数估计和模型检验等，具体步骤简述如下：

（1）对序列进行平稳性检验。

（2）根据AIC和SC准则确定模型线性部分AR模型的最优阶数p。

（3）由于转移函数G(·)中参数γ不可识别，线性检验和滞后阶数d的确定需要将其泰勒展开，三阶泰勒展开式如式（4）所示：

线性检验需对假设 H0:β2j=β3j=β4j=0进行检验，如果拒绝原假设就应该建立STAR模型，反之，建立线性模型。滞后阶数的确定是选取拒绝原假设最强烈（p值最小）的d。

（4）由于LSTAR模型和ESTAR模型的三阶泰勒展开式不同且是嵌套的，所以非线性模型形式的确定需要进行如式（5）的嵌套检验，计算上述三个式子中的所有的F或者χ2检验的p值，并且选择具有最小的p值对应的STAR模型为所需要的模型。即如果拒绝H04或H02对应的 p值最小，则应该选择LSTAR模型；如果拒绝H03对应的 p值最小，则应该选择ESTAR模型：

（5）使用基于最小误差平方和法和循环推测法（改进的Gauss-Newton法）的非线性最小二乘估计对选择的模型进行参数估计。

（6）检验模型。对模型的残差进行自相关、异方差和正态性检验。

2 样本数据选取及实证分析

本文选取居民消费价格指数（CPI）、商品零售价格指数（RPI）、生产者出厂价格指数（PSPI）和生产者购进价格指数（PBPI）四类价格指数作为衡量物价水平的指标，鉴于数据可得性和样本区间选取的一致性，样本区间为1996年10月至2014年11月,样本容量为218，数据来自国家统计局官方网站。

为了很好的观察四类价格指数的波动特征，绘制其折线图如下图1所示。观察图1容易看出四类价格指呈现出非常复杂的同升同降的周期性波动特征，且PBPI和PSPI的波动幅度显著大于CPI和RPI的波动幅度。仔细观察还可发现，四类价格指数在上行和下行过程中呈现出上行缓慢下行迅速的非对称特征。这些都暗示出四类价格指数具有非对称的非线性波动特征。

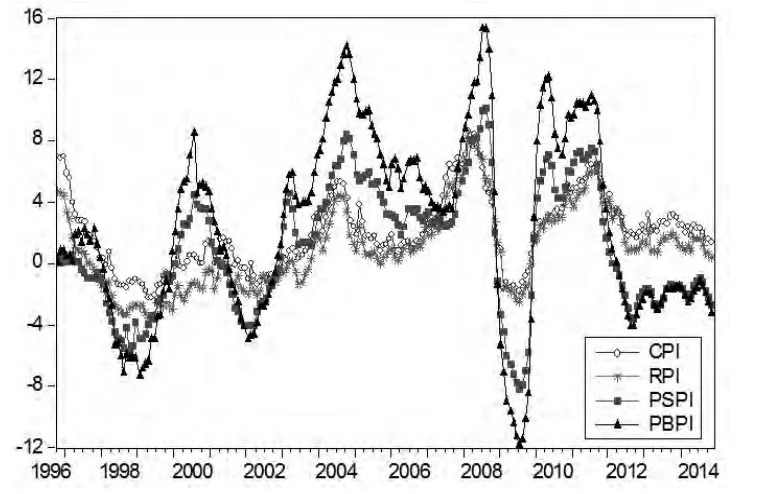
图1 四类价格指数折线图

按照STAR模型的建模步骤，首先对四个序列进行平稳性检验可得ADF检验统计量值分别为-2.28、-2.39、-3.58和-3.51，相依概率为0.0221、0.0166、0.0004和0.0005，小于0.05的显著性水平，说明四个序列是平稳序列，可以直接用来进行STAR模型建模。

其次，确定AR模型的阶数p。多次估计模型并比较不同模型下的AIC和SC，最终得到各序列确定的最终模型如下表1所示。从表1可以看出，四个序列确定的最终模型各不相同。RPI序列最终确定的AR模型的残差正态性、自相关性和异方差性检验统计量对应的 p值 pJB、pLM和 pARCH均大于0.05，说明RPI序列对应的AR模型的残差通过了正态性、无自相关和无异方差检验，模型拟合效果良好。其他三序列最终确定的AR模型对应的残差检验中只有自相关检验统计量对应的p值pLM大于0.05，正态性检验和异方差检验统计量对应的p值pJB和pARCH均小于0.05，说明模型残差存在异方差和非正态性，这充分说明线性模型对其序列信息提取不够充分，这很有可能是因为序列中存在非线性成分所导致的后果。

表1 各序列最终确定的AR模型及模型检验结果

接下来，进行线性检验，我们考虑将原始序列的滞后1至15期序列作为转换变量进行线性检验，选取线性检验所得的χ2值和F值对应的最小的p值作为转移变量，所得结果如表2所示。从表2可以看出CPI和RPI序列最终确定的转移变量为其原始序列的滞后10期序列，PSPI和PBPI序列最终确定的转移变量为其原始序列的滞后3期和4期序列。

进而，确定模型的形式，按照上文所述，经计算可得各序列H04、H03和H02三个假设对应的 χ2值、F值及其所对应的p值如表3所示。从表3中可以看出四个序列适合的STAR模型并不完全相同。CPI序列中，拒绝假设H02的 p最小，因此对CPI序列应该建立LSTAR模型；其余三序列中，均是拒绝假设H03的 p最小，因此这三个序列应该建立ESTAR模型。

表2 各序列最终确定的转移变量及其线性检验统计量的值

表3 各序列嵌套检验结果

接着，分别估计四个序列对应的STAR模型，模型中转移参数和阈值参数估计结果如表4所示。从表4估计结果可以看出，CPI、RPI、PSPI和PBPI的转移参数逐渐增大，分别为12.768、18.915、28.916和35.658。这说明居民消费物价指数由低区制转移至高区制速度最慢，商品零售物价指数次之、进而是生产者出厂物价指数、生产者购进物价指数最快。究其原因，生产者较零售商和消费者而言所能掌握的市场信息较多且其对价格调整较为容易，因此其对价格的反映最为敏感，故由低区制转移至高区制的速度最快。同样原因，商品零售物价指数由低区制转移至高区制速度次之，居民消费物价指数由低区制转移至高区制速度最慢。而PBPI较PSPI的转移速度快是因为当生产资料价格上升时生产者购进物价指数会迅速上升，而由于生产者在售出商品时具有一定主动性，因此其可以根据市场环境来调整商品出厂价格，故生产者购进物价指数由低区制转移至高区制的转移速度要大于生产者出厂物价指数。阈值参数按RPI、CPI、PSPI和PBPI顺序依次增大，这可能是由于四类物价指数取值和波动幅度按其顺序逐渐增大所致。

表4 各序列模型中转移参数和阈值参数估计值

最后，对各序列对应模型的残差进行正态性、自相关和异方差检验可得如表5所示。从表中可以看出四序列对应模型的残差正态性、自相关和异方差检验的统计量对应的p值均远远大于0.05的显著性水平，说明模型残差通过了正态性、无自相关和无异方差检验，模型拟合效果良好。比较表1和表5线性模型和非线性模型的残差检验可以看出，各序列对应的非线性模型的残差平方和SSR较线性模型而言有很大程度的降低，且非线性模型残差检验各统计量对应的p值均远远大于线性模型中残差检验各统计量对应的 p值，这充分说明非线性模型拟合效果要远远好于线性模型的拟合效果，四类价格指数的数据生成过程为非线性STAR模型。

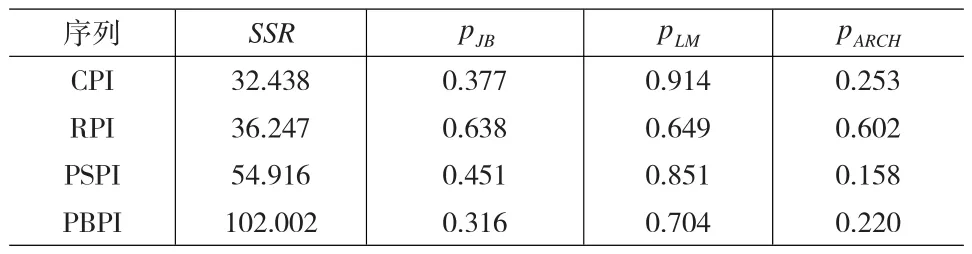
表5 各序列模型残差检验结果

3 结论与启示

本文运用STAR模型对代表我国物价水平的四类价格指数的非线性波动特征进行了验证和建模分析，得到结论和启示如下：

（1）从四类价格指数来看，我国物价水平波动具有非线性特征。但四类价格指数数据生成的非线性机制不同，居民消费价格指数为LSTAR模型、其他三类价格指数为ESTAR模型，这说明居民消费价格指数在非线性波动中呈现出非对称的非线性转移特征，而其他三类价格指数在非线性波动中呈现出对称的非线性转移特征。

（2）从转移变量来看，CPI和RPI为自身变量的滞后10期序列，而PSPI为其自身变量的滞后3期序列，PBPI为其自身变量的滞后4期序列。说明CPI和RPI的结构转换发生在自身滞后10期，而PSPI结构转换发生在自身滞后3期，PBPI的结构转换发生在自身滞后4期。

（3）从模型参数估计结果来看，CPI、RPI、PSPI和PBPI四序列的转移参数依次增大，分别为12.768、18.915、28.916和35.658，这说明生产者对价格反应的灵敏程度最强，零售商次之，消费者最差；另外，RPI、CPI、PSPI和PBPI四序列的阈值参数依次增大，分别为2.583、3.624、4.013和4.972，这很可能是由于四个序列波动程度依次增大所致。

（4）从线性模型和非线性STAR模型的拟合结果来看，非线性STAR模型拟合结果明显优于线性模型，说明在对我国物价水平进行分析预测时应该选用非线性STAR模型才能取得理想效果。

[1]Engle R F．Estimates of The Variance of US Inflation Based on The ARCH Model[J].Journal of Money,Credit and Banking,1983,(15).

[2]冼国明,石庆芳.人民币汇率波动对中国物价水平的影响——汇率制度变迁视角[J].财贸研究，2014，（4）．

[3]任泽平.能源价格波动对中国物价水平的潜在与实际影响[J].经济研究，2012，（8）．

[4]刘文涛.中国信贷投入与物价水平的实证研究[J].统计与决策，2012，（20）

[5]王飞,孙维尧.际大宗商品价格与国内物价水平的影响关系研究—基于美国量化宽松货币政策环境下的分析[J].价格理论与实践，2013,（1）．