EKF算法在远程炮位侦察校射雷达中的应用研究

梁开莉，时荔蕙，程兴亚

(解放军63961部队， 北京100012)

0 引言

炮位侦察校射雷达通过捕获一段弹丸的飞行轨迹，外推炮位的发射点或弹着点，不要求与目标通视，并且具有全天候、全天时等优点，是重要的侦察装备，其发展引起广泛关注。随着雷达作用距离的增加，远程炮位侦察校射雷达弹道外推出现了新特点。图1是弹道外推问题的说明示意图:火炮位于O1点，雷达位于O2点，发射直角坐标系O1XPYPZP和雷达观测直角坐标O2XRYRZR相距较远。从图中可知，由于地球曲率的影响，在雷达观测直角坐标系中观察到的数据，已经不能用发射直角坐标系中的弹道模型来描述，其YR轴不能代表弹道飞行的真实高度Yp，也不能代表对应的大气高度。因此，雷达观测直角坐标系和发射直角坐标系之间不能采用传统的坐标平移来实现［1-3］。远程炮位侦察校射雷达如果继续沿用近程炮位侦察校射雷达外推算法其外推精度将变差并最终不可接受。针对该问题，我们进行了远程弹道外推方法研究。由于弹道外推的过程如下，首先对雷达观测到的一段弹道数据进行滤波，将测量误差的影响减到最小，然后根据弹道运动方程，采用龙格-库塔法外推发射点坐标。因此外推弹道的关键是弹道滤波方法和弹道运动方程的选取。

图1 远程炮位侦察校射雷达弹道外推

1 弹道方程的选取

在近程炮位侦校中，弹道方程采用直角坐标系下的质点方程，而且重力加速度不变，如下面方程所示［4-6］

而在远程弹道侦校中，由于飞行点距离雷达远，所以必须考虑地球曲率的影响，同时要考虑飞行高度对重力的影响。

在雷达切平面直角坐标系中，考虑到地球的曲率影响，弹道飞行的质点方程表示为［5-6］

第四项表示科氏加速度在x、y、z三个轴上的分量，科氏加速度的矢量表示为ak=2Ω×v，即将地球的自转速度分解到x、y、z三个轴上，再与弹道目标的三个速度分量进行叉乘得到，Ω为地球自转角速度，Λ为纬度，α为射向角。

2 EKF弹道滤波

2.1 EKF弹道滤波的实现过程

EKF滤波理论比较成熟，这里只介绍滤波流程，如图2所示［7-11］。从图中可以看出，EKF滤波在动力学方程已经选定的情况下，关键技术变成了A、F、观测矩阵的估计值、预测的协方差矩阵、增益矩阵等矩阵的求取，因此本文对A、F矩阵进行推导。

图2 EKF滤波过程

2.2 远程弹道EKF滤波关键项计算

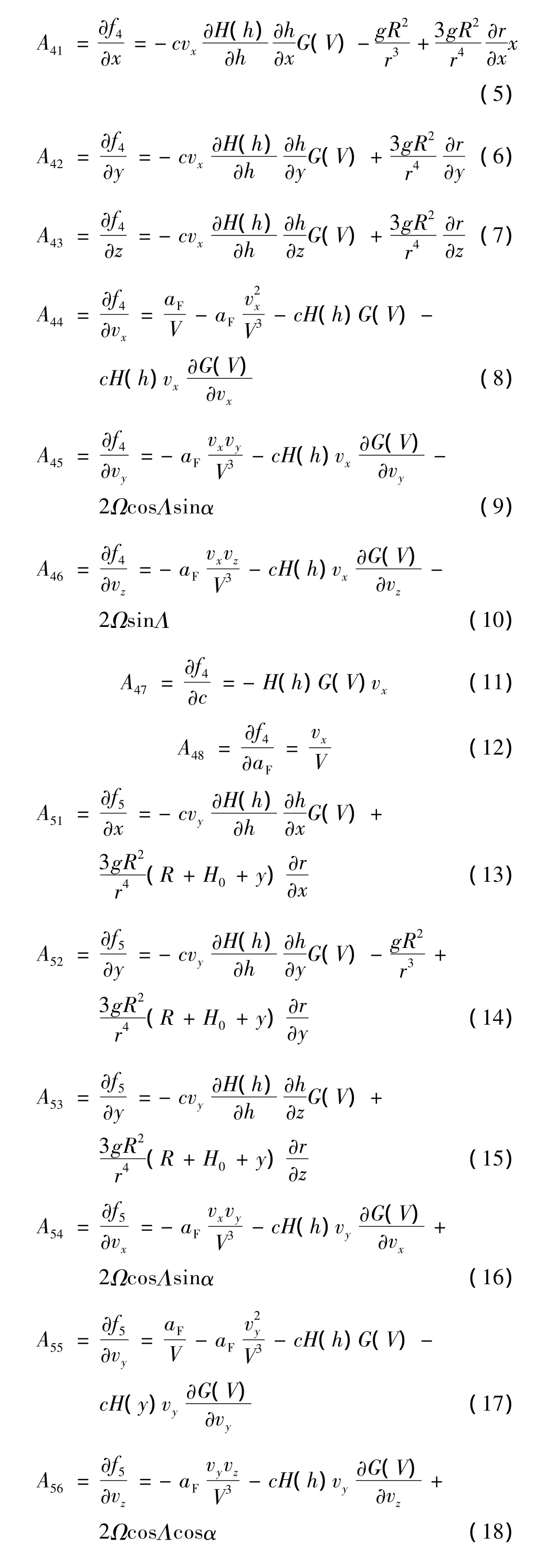
3 实测与仿真数据验证

采用仿真数据进行验证，得到的外推精度如图3所示，从图中可以看出，近程雷达算法精度在100 km处的误差超过300 m，而本文提出的EKF算法误差仅为108 m，EKF算法精度远远优于近程算法精度。仿真数据说明远程炮位侦察校射雷达采用远程算法的必要性和有效性。

图3 EKF算法同近程雷达算法的仿真数据效果比较

采用某雷达9发榴弹炮实测数据进行验证，外推结果如图4所示，以目标点为中心，0.25%R(火炮雷达距离)为半径画圆，外推9发炮位数据全部落在圆内，外推结果CEP误差为0.24%R，证明了算法的有效性。

图4 远程炮位侦察校射雷达测量数据外推结果

4 结束语

对远程炮位侦察校射雷达弹道外推，如果继续沿用近程炮位侦察校射雷达外推算法其外推精度将变差得不可接受。更好的方法是，在雷达切平面直角坐标系中，选用弹道飞行的质点方程，同时考虑到地球的曲率影响，以及采用 ¯x=［x，y，z，vx，vy，vz，c，a］T8 状态矢量进行EKF滤波，可以将测量误差的影响减到最小。对本文提出的算法，我们进行了实测与仿真数据验证，发现无论是仿真数据还是实测数据的外推结果都能够满足外推精度要求，因此，本文提出的算法可以在工程实现中采用，具有很强的实用性。

［1］单 奇，钮俊清，李 川.炮位侦校雷达的数据处理研究［J］.雷达科学与技术，2010，8(2):171-176.Shan Qi，Niu Junqing，Li Chuan.Study on data processing of firefinder radar［J］.Radar Science and Technology，2010，8(2):171-176.

［2］荣长军，李志刚，徐 新，等.火炮射击偏差校正系统［J］.火力与指挥控制，2008，33(增刊):11-13.Rong Changjun，Li Zhigang，Xu Xin，et al.Research on shooting correction of artillery［J］.Fire Control and Command Control，2008，33(S1):11-13.

［3］游凤平.相控阵炮位雷达多目标处理软件仿真［J］.现代雷达，2011，33(3):28-33.You Fengping.Multiple-target simulation software of fire finding phased array radar［J］.Modern Radar，2011，33(3):28-33.

［4］ 徐明友.高等外弹道学［M］.北京:高等教育出版社，2003.Xu Mingyou.Higher exterior ballistics［M］.Beijing:Higher Education Press，2003.

［5］ 宋丕极.枪炮与火箭外弹道学［M］.北京:兵器工业出版社，1993.Song Piji.Firearms and rocket exterior ballistics［M］.Beijing:Weapon Industry Press，1993.

［6］浦 发，张 枌.外弹道学［M］.北京:国防工业出版社，1980.Pu Fa，Zhang Feng.Exterior ballistics［M］.Beijing:National Defense Industry Press，1980.

［7］付梦印，邓志红，闫莉萍.Kalman滤波理论及其在导航系统中的应用［M］.2版.科学出版社，2010.Fu Mengyin，Deng Zhihong，Yan Liping.Kalman filter theory and apply in navigation system［M］.2nd ed.Beijing:Science Press，2010.

［8］何 友，修建娟，张晶伟，等.雷达数据处理及应用［M］.北京:电子工业出版社，2006.He You，Xiu Jianjuan，Zhang Jingwei，et al.Radar data processing with applications［M］.Beijing:Publishing House of Electronics Industry，2006.

［9］ 宋文尧，张 牙.卡尔曼滤波［M］.北京:科学出版社，1991.Song Wenyao，Zhang Ya.Kalman filter［M］.Beijing:Science Press，1991.

［10］张先萌，王建新.卡尔曼滤波器在炮位侦察雷达中的应用［J］.南京理工大学学报:自然科学版，1987(3):67-72.Zhang Xianmeng，Wang Jianxin.Apply of Kalman filter in fire finding radar［J］.Journal of Nanjing University of Science and Technology:Natural Science，1987(3):67-72.

［11］欧阳杰，王成绪.协方差分析描述函数法在火箭导弹统计性能分析中的应用［J］.兵工学报，1981(2):10-32.Ouyang Jie，Wang Chengxu.The apply of the covariance analysis describing function technique on the rocket missile statistical performance analysis［J］.Acta Armamentarii，1981(2):10-32.