规避机动对雷达检测概率的影响研究

林存坤，张小宽，刘 铭，张晨新

(空军工程大学 a.防空反导学院； b.科研部， 西安710051)

0 引言

现代战争中，飞机为突防敌方阵地，摆脱防空导弹的打击，一般在被地面雷达跟踪或防空导弹锁定后紧急采取规避机动。虽然实施规避机动的作战场景各不相同，但都是通过不断改变飞行方向、速度、高度等来获得较大的生存概率和突防概率。常采用的规避机动有蛇形机动、盘旋、8字形巡逻、水平急转弯机动等。

文献［1-2］对常用的典型机动如定直平飞、俯冲、跃升、水平急转弯、蛇形机动、8字巡逻等做了大量细致的航迹建模仿真。文献［3］研究了隐身目标对雷达探测的影响，但所用雷达散射截面(RCS)是模拟生成的随机量，缺乏真实性。文献［4］仿真了盘旋机动的动态RCS，分析了动静态RCS统计模型对检测概率的不同影响，得出了动态RCS时间序列包含了比静态RCS更真实丰富的目标雷达特性信息的结论。本文以某型战斗机为研究对象，运用飞行动力学原理建立了水平急转弯机动和蛇形机动航迹模型，再由目标实时姿态、位置等信息得到目标的实时雷达视线角，结合已建立的全空域静态RCS特性库，解算出目标的动态RCS序列，数据真实可信;然后，利用起伏目标的检测原理［5］，研究了目标的瞬时检测概率;最后，从检测概率角度定性分析了两种机动对生存和突防效率的影响。

1 目标规避机动模型

1.1 飞行动力学原理

本文采用文献［4］中的常用坐标系和姿态角定义。基于飞行器航迹坐标系下的质心动力学方程［6］，建立了飞机规避机动模型。不考虑侧滑角和侧力项时，质心动力学方程［2］可表示为

式中:v为飞行器质心对地速度;g为重力加速度;θa、Ψa分别为航迹倾角和航迹偏角;φa为速度滚转角;nx、ny分别为切向、法向过载。其中，φa、nx、ny为控制变量。

1.2 水平急转弯机动

飞机在下述两种情况下采用水平急转弯机动:(1)当飞机发现正在被防空导弹拦截时，为摆脱拦截进行机动;(2)飞机投弹后，为迅速脱离敌方防区进行机动。飞机在低空、中空、高空都可进行这种机动。

下面分别设计了三种高度下的水平急转弯机动模型。为简化模型，假定飞机作匀速飞行，且将水平急转弯机动简化分成三段飞行阶段即匀速向站直线飞行阶段、匀速急转弯阶段、匀速背站直线飞行，其中第一、三段均为匀速飞行阶段，航迹倾角θa、航迹偏角Ψa均为零，飞行过程较为简单，仅由式(2)就可得到飞行航迹。第二段水平匀速转弯运动可以近似看成匀速圆周运动，其动力学模型应满足［5］

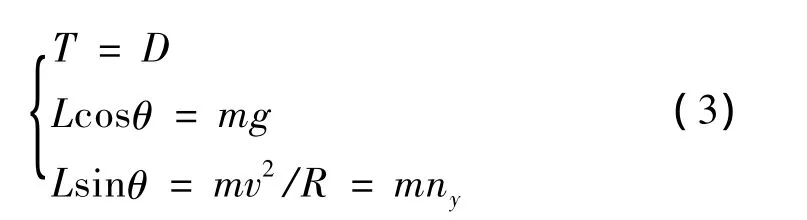
式中:T为推力;D为空气阻力，由T=D可得nx=0;L为空气升力;θ为飞行坡度，在此飞行过程中也为飞机滚转角。因此，只要给定不同高度下的法向过载ny和飞行速度v，就可联立式(1)、式(2)、式(3)，建立水平急转弯机动模型。

仿真中第一、三段飞行时间均设为10 s，飞机初始位置距雷达水平距离50 km，初始航路捷径为零。图1以低空水平急转弯为例，给出了飞行航迹图和航迹偏转角、滚转角变化情况图。表1列出了本文采用的水平转弯段机动参数。

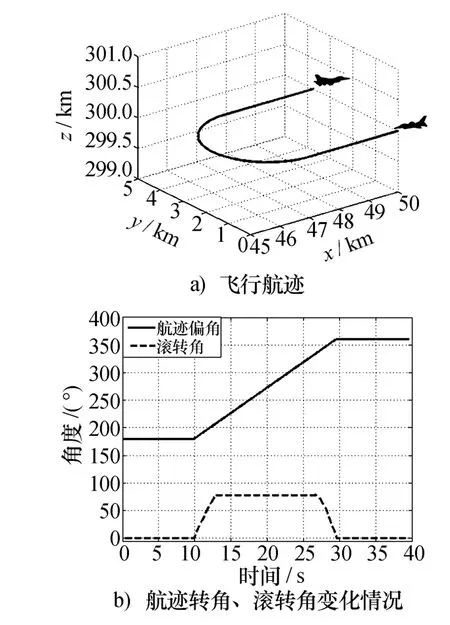
图1 低空水平急转弯机动

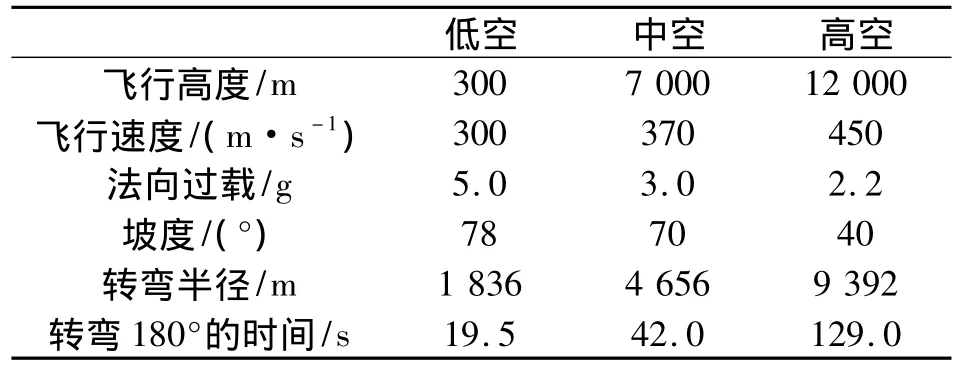
表1 三种高度下水平转弯段的机动参数

1.3 蛇形机动

蛇形机动是一种较为常用的反雷达、反导弹机动，主要用在防区突防和脱离防区，即在进入轰炸航路前或投弹后脱离时采取机动，目的在于增加雷达的探测跟踪误差，也可在被防空导弹锁定后，做此机动增加导弹飞行过载，降低命中概率［1］。

由于飞机在突防时，主要在低空进行蛇形机动，因此本文只研究了低空蛇形机动(选定高度为300 m)。类似于水平急转弯机动，蛇形机动可以简化为匀速直线飞行和匀速转弯飞行［7］。参照文献［2］在蛇形机动仿真中采用的切向和法向过载，本文仿真用到的nx、ny如图2所示。联立并求解式(1)、式(2)即可得到蛇形机动模型。具体仿真条件设为:飞行速度300 m/s，左右转弯时偏离主航向的角度为20°，初始时刻距雷达水平距离50 km，得到的蛇形机动航迹和航迹偏角、滚转角变化如图3所示。

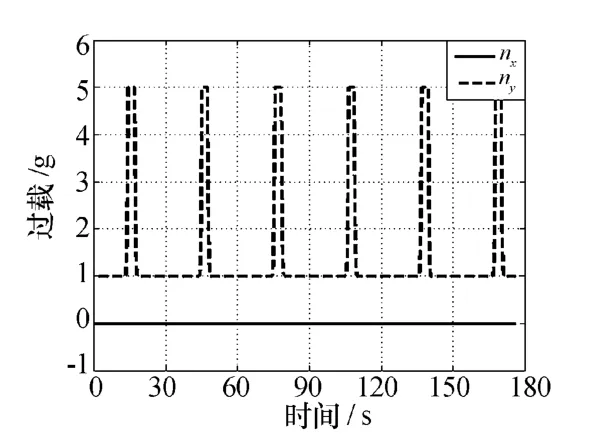
图2 法向、切向过载变化情况

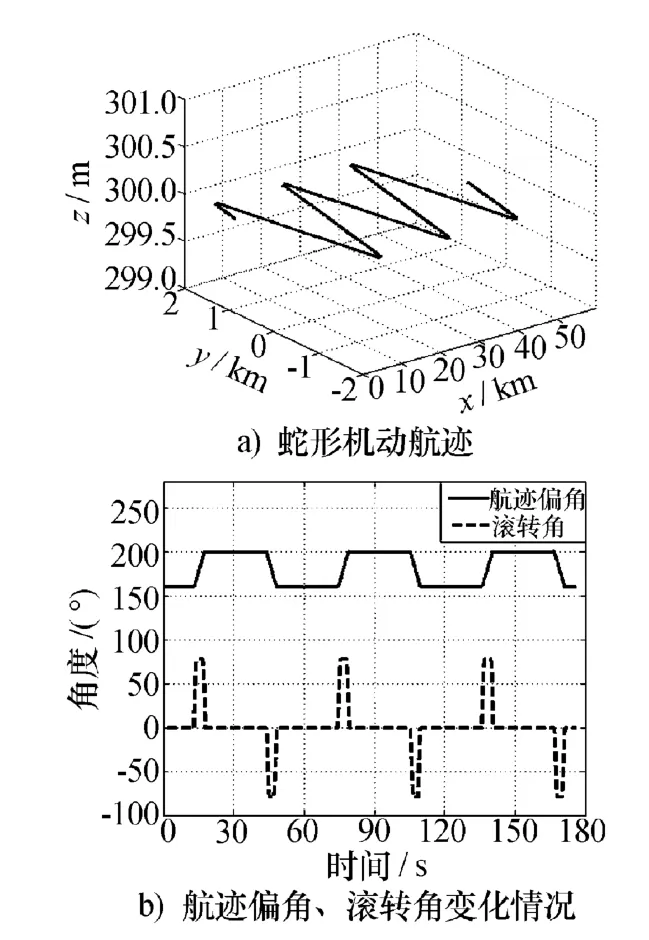
图3 蛇形机动

2 动态RCS时间序列

2.1 全空域静态RCS特性数据库

采用电磁场仿真软件FEKO对目标静态RCS特性进行仿真，选用矩量法仿真计算了目标的全空域静态 RCS 特性库［8］。仿真条件为 181°×361°全空域入射角，角度间隔取1°，频段为C波段。目标的静态全空域RCS如图4所示。由图4可得，该飞机头部、尾部的RCS明显低于机腹、机背的RCS。

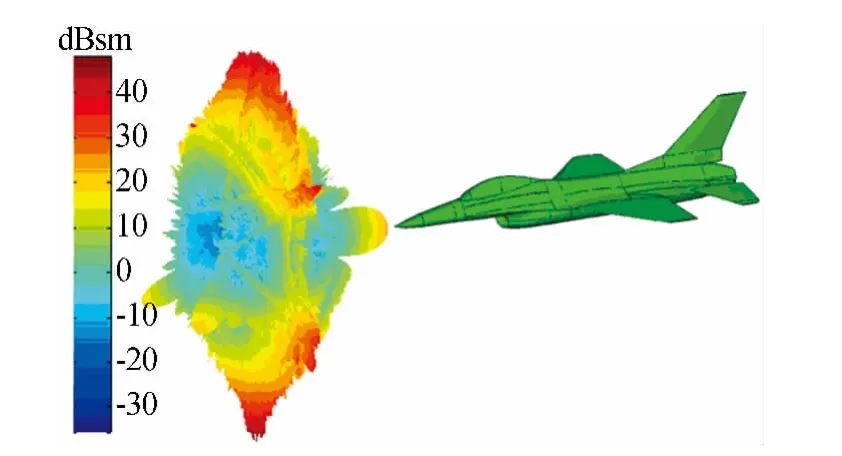
图4 目标静态全空域RCS

2.2 雷达视线角

根据建立的目标规避机动模型，得到了目标的实时姿态、位置等信息，进而解算目标的实时雷达视线角。雷达视线角求解算法［9］如下

式中:x1(t)，y1(t)，z1(t)分别为雷达在机体参考坐标系下的坐标;x(t)，y(t)，z(t)分别为雷达在机体坐标系下的坐标;θ、Ψ、γ分别为目标的姿态角为俯仰角、偏航角、滚转角。其中，机体参考坐标系的定义为雷达坐标系的坐标原点到机体中心的平移。雷达视线在机体坐标系中的方位角φ(t)和俯仰角θ(t)为

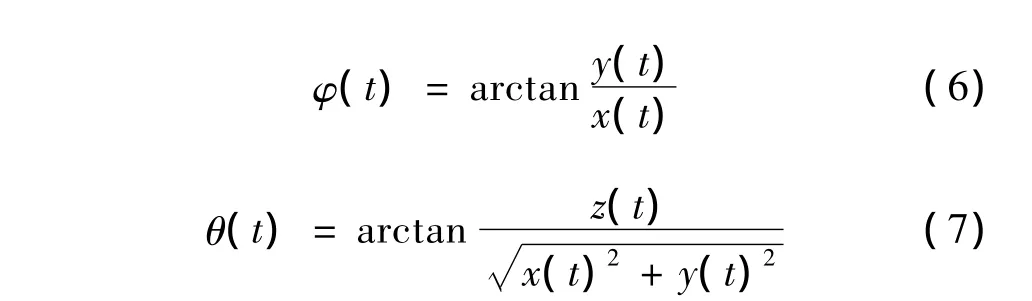
结合水平急转弯目标机动信息，由式(4)～式(7)可以求出飞机作水平急转弯机动(以低空为例)和蛇形机动时的雷达视线角方位角和俯仰角变化情况，如图5、图6所示。

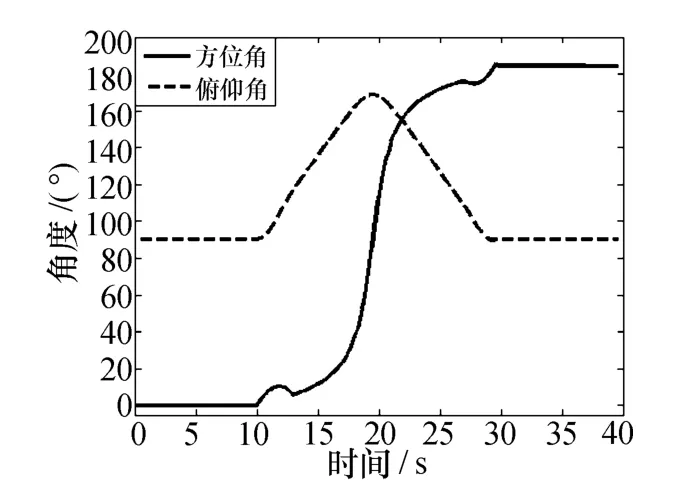
图5 水平急转弯机动雷达视线角变化情况

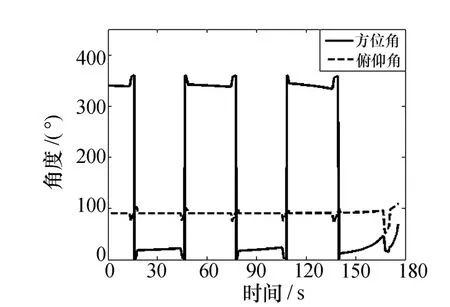
图6 蛇形机动雷达视线角变化情况

2.3 动态RCS时间序列

根据目标的实时雷达视线角，结合已建立的全空域静态RCS特性库，解算出了目标的动态RCS序列。图7a)～图7d)分别为低空、中空、高空水平急转弯机动和低空蛇形机动的动态RCS时间序列。

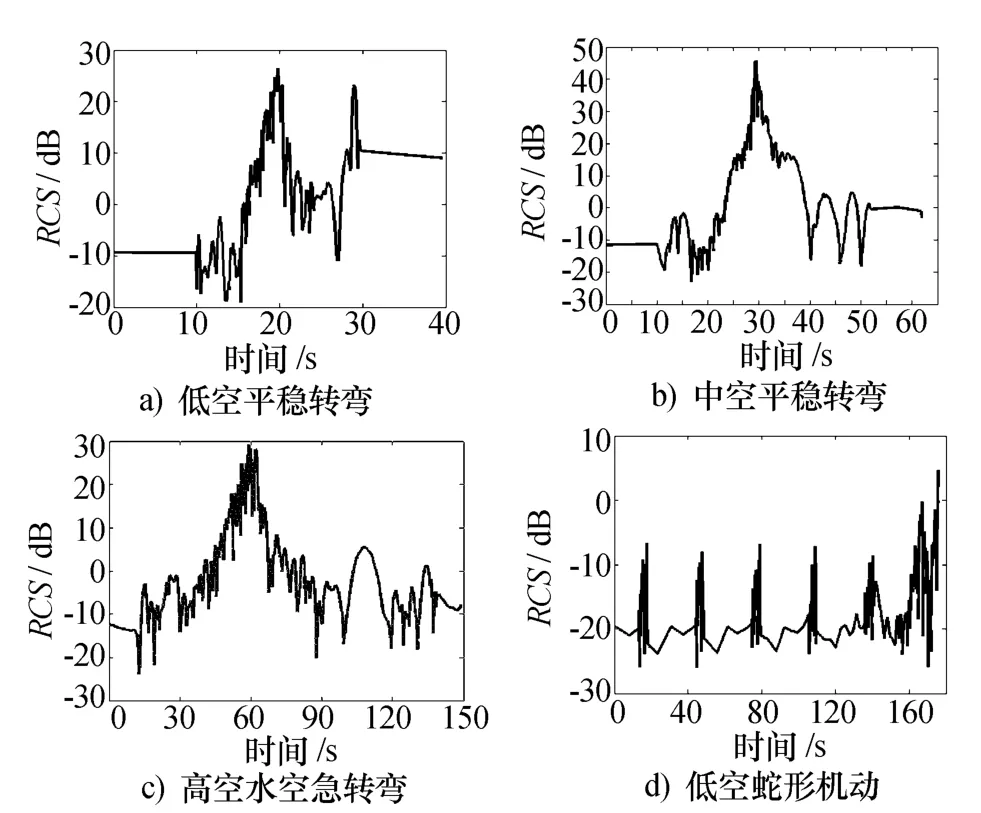
图7 动态RCS时间序列

3 规避机动对检测概率的影响

单脉冲积累下，由雷达方程式可以得到可检测信号强度

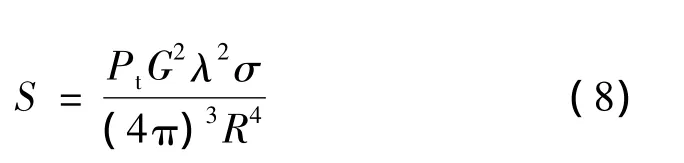
式中:Pt，G，λ分别为雷达的峰值发射功率、天线增益、脉冲波长。对于给定雷达，这些雷达参数都是已知的。假定背景杂波服从高斯分布，经平方律检波后，噪声功率可以看成是一个常数［3］。

Swerling将起伏目标划分为四种不同的Swerling模型，其中SwerlingⅠ型目标在一次天线扫描期内具有恒定的幅度，而不同扫描期间起伏幅度按照两个自由度的χ2概率密度函数独立变化［10］，即认为同一扫描期内各发射脉冲下的RCS相同。因此考虑多脉冲相参积累时，积累后信噪比为

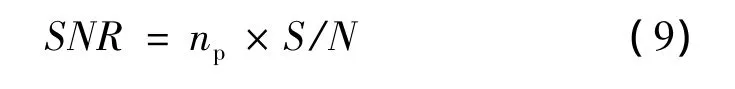
式中:np为相参积累脉冲数;N为噪声强度。当np一定时，信噪比SNR仅与目标的RCS和目标距雷达距离R有关。

本文采取SwerlingⅠ型模型分析规避机动RCS起伏对检测概率的影响。检测概率的公式［7］为

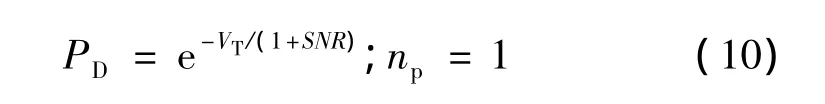
式中:VT为检测门限，可以由Newton-Raphson方法中的递归算法求解。

图8给出不同高度下雷达对水平急转弯机动目标的检测概率。图9为雷达对相同飞行距离段蛇形机动与匀速直线飞行时目标的检测概率。

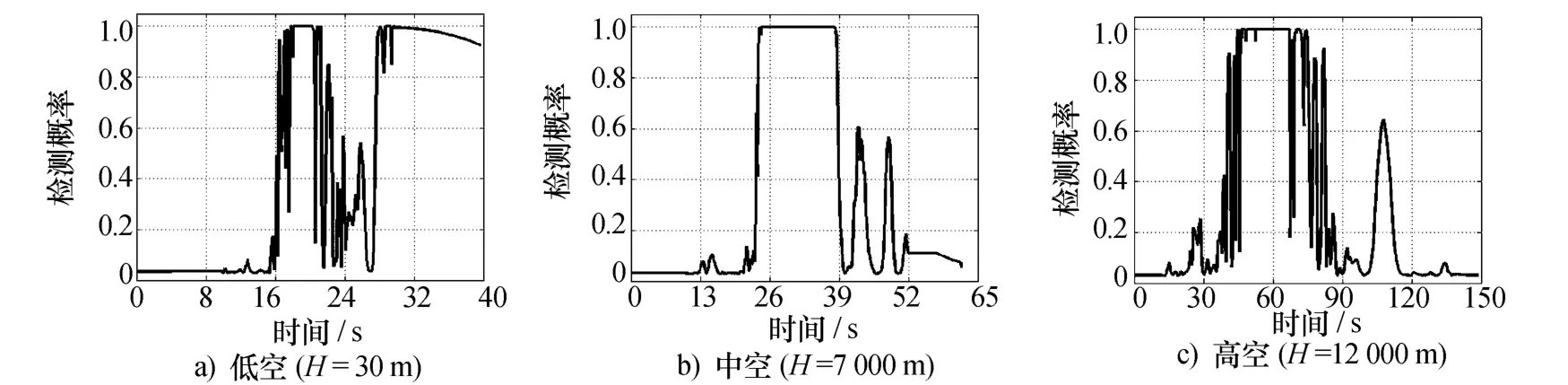
图8 水平急转弯机动的检测概率

从图8中分析可知，在水平急转弯机动的前期，雷达检测概率都较低，这是由于飞机对站飞行，头向RCS较小。在转弯阶段，检测概率都较大，因为此时雷达波束照射飞机机腹，RCS较大。之后的背站飞行段，雷达检测概率出现较大差别，低空时的检测概率较大，中空和高空时较小，这也与图7所示的动态RCS变化趋势相同。

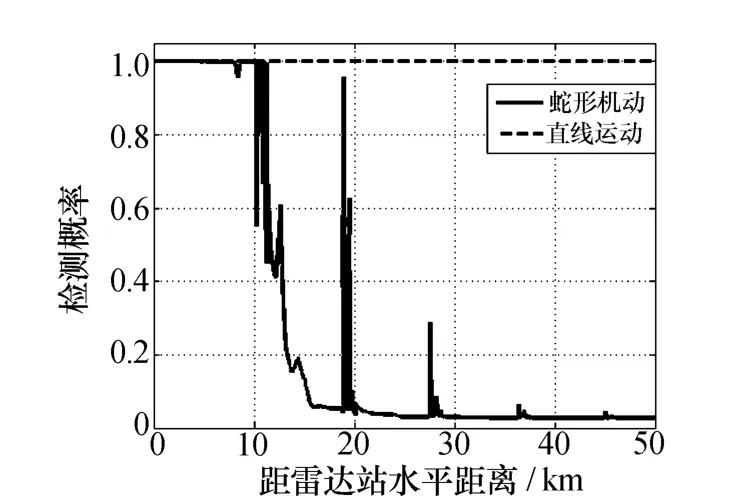
图9 蛇形机动的检测概率

对图9中两条检测概率曲线比较分析可知，蛇形机动在距雷达站较远距离时，检测概率很低，虽然在转弯段，RCS出现较大值，检测概率有起伏，但转弯时间较短，与不做机动时检测概率近似为1相比，此时蛇形机动起到了较好的突防效果。但随着飞机突防的纵深，检测概率几乎与不做机动时一样，即距雷达距离R成为影响检测概率的主要因素，这也是与实际相符的。

4 结束语

本文通过建立两种典型规避机动模型，研究了目标机动对雷达检测概率的影响。该研究为飞机在突防作战时，如何采取规避机动提供了仿真依据，具有一定的实用价值。

［1］ 王 嘉.几种典型机动动作的自动飞行仿真研究［D］.西安:西北工业大学，2007.Wang Jia.Study on automatic flight simulation of several typical maneuvers［D］.Xi＇an:Northwestern Polytechnical University，2007.

［2］ 李世鹏，高正红.飞机机动指令生成器设计及蛇形机动仿真［J］. 飞行力学，2005，23(2):19-22.Li Shipeng，Gao Zhenghong.Design of a maneuver generator and S maneuver simulation［J］.Flight Dynamics，2005，23(2):19-22.

［3］ 杨 波，杨建涛，李春鹏.雷达探测隐身飞机仿真［J］.中国科技信息，2011(14):29-30.Yang Bo，Yang Jiantao，Li Chunpeng.Simulation of radar detection of stealth aircraft［J］.China Science and Technology Information，2011(14):29-30.

［4］ 戴 崇，徐振海，肖顺平.雷达目标动静态RCS特性差异分析［J］.信号处理，2013，29(9):1256-1263.Dai Chong，Xu Zhenhai，Xiao Shunping.Analysis for differences between dynamic and static RCS characteristics of radar target［J］.Journal of Signal Processing，2013，29(9):1256-1263.

［5］ 刘思源，张 蕾，姚佩阳，等.战术飞行机动动作仿真设计与实现［J］.空军工程大学学报:自然科学版，2011，12(5):30-33.Liu Siyuan，Zhang Lei，Yao Peiyang，et al.Tactical air maneuver simulation design and implementation［J］.Journal of air Force Engineering University:Natural Science Edition，2011，12(5):30-33.

［6］ 高 浩，朱培申，高正红.高等飞行动力学［M］.北京:国防工业出版社，2004.Gao Hao，Zhu Peishen，Gao Zhenghong.The advanced flight dynamics［M］.Beijing:National Defense Industry Press，2004.

［7］ Remzi A，Altilar D T.Modeling evasion tactics of a fighter against missile in three dimensions［R］.AIAA-2006-6604.Keystone Cadorado:AIAA，2006.

［8］ Li X R，Jilkov V P.Survey of maneuvering target trackingpart I:dynamic models［J］.IEEE Transactions on Aerospace and Electronic System，2003，39(4):333-1364.

［9］ 袁国华，张伟丽，闰学勤，等.动态RCS数据处理中的视向角求解算法［J］.航空武器，2011(2):13-19.Yuan Guohua，Zhang Weili，Yan Xueqin，et al.Arithmetic for line of sight in dynamic RCS data processing［J］.Airborne Weaponry，2011(2):13-19.

［10］ Mahafza B R，Elsherbeni A Z.雷达系统设计MATLAB仿真［M］.北京:电子工业出版社，2009.Mahafza B R，Elsherbeni A Z.MATLAB simulation for radar systems design［M］.Beijing:Publishing House of E-lectronics Industry，2009.