求解二阶锥互补问题的预估校正算法＊

张襄松，周宏安

（西安工业大学 理学院，西安710021）

二阶锥互补问题（SOCCP）是指寻找向量x∈Rn使

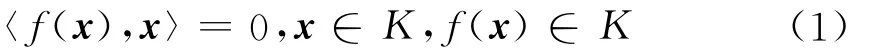
成立，其中〈·，·〉表示欧几里德内积，f是连续可微映射．K是二阶锥上的笛卡尔积，即

K＝Kn1×Kn2×…×Knm

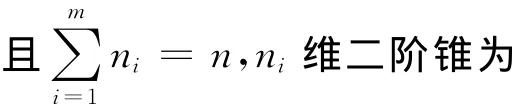
其中‖·‖表示欧几里德范数．

特别地，当ni＝1，（i＝1，…，m）时，二阶锥互补问题等价于非线性互补（Nonliear Comple mentarity Problems，NCP）问题．

在研究二阶锥规划的库恩-塔克条件（Karush Kunh Tucker Conditions，KKT）和许多实际问题时，经常会面临二阶锥互补问题［1-2］，因此给出可行有效的方法来求解二阶锥互补问题成为近年来的研究热点之一．类似于非线性互补问题和半定互补问题［3-4］，一个途径就是基于一个适合的互补函数将其转化为Rn上的某个价值函数的无约束最小化问题或一个非线性方程组来求解．目前，求解这类问题方法主要有内点算法、光滑方法等．其中由于内点算法在求解许多数学规划问题时都被证明具有多项式计算复杂性，使得该算法在求解尤其是大规模优化问题具有优势，但是现有的内点算法对初始点的选取却相对苛刻，一般要求初始点是严格可行的，然而对许多实际问题，找到严格可行的初始点并不容易．而近年来由于良好的性能而受到关注的光滑方法，则可以弥补这种不足：光滑化方法对初始点的选取没有严格要求，并且在算法实施的过程中，也不需要内点的限制，因此，光滑化方法成为求解优化问题特别是互补问题的一种颇受青睐的方法．求解二阶锥互补问题方法主要有内点算法、光滑方法等．内点算法是求解二阶锥规划的一类非常重要的算法，这类算法的优点在于它具有多项式计算复杂性，适合于大规模问题的计算，但是现有的内点算法大多数要求初始点是严格可行的，然而许多实际问题难以直接找到严格可行的初始点．另一方面，近年来出现的光滑方法，由于其良好的性能而受到优化问题研究者的极大关注，这类方法与内点法不同的是光滑化方法可以任意选取初始点，并且在算法实施的过程中，不需要内点的限制，因此，光滑化方法成为求解优化问题特别是互补问题的一种颇受青睐的方法．

本文通过对Fischer-Burmeister互补函数进行对称扰动，得到了一个新的光滑函数，利用得到的光滑函数，把二阶锥互补问题转化为一个非线性方程组问题，给出求解单调二阶锥互补问题的预估校正光滑算法．文中所有向量均为列向量，R＋＋表示非负实数集，T表示向量或矩阵的转置，I表示一个适当维数的单位矩阵．可微函数f：Rn→Rn在点x的梯度记作▽f（x）．intK表示K的内部，x≻y表示x-y∈intK．

1 预备知识

若当代数是研究二阶锥问题的有力工具［1］．在若当代数J中，对任意向量

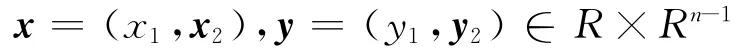
可定义若当积

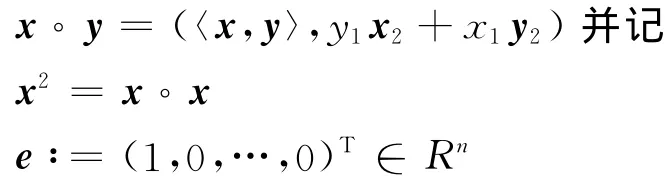
x＋y表示通常意义下的加法．给定若当代数中一个向量x，定义一个对称矩阵

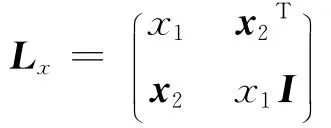
其中I表示n-1阶的单位阵．

定理1 （谱分解定理［1］）

对向量x＝ （x1，x2）∈R×Rn-1，与二阶锥相伴的谱分解定义为x＝λ1u（1）＋λ2u（2）．其中

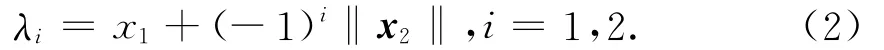
谱向量为

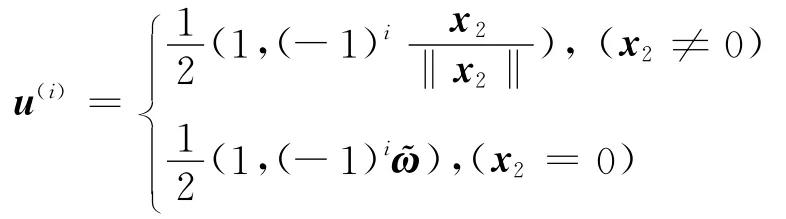
下面给出任意一个向量x的谱分解的基本性质．

性质1 对任意向量x∈Rn，它的谱值λ1，λ2和谱向量u（1），u（2）分别由式（2）和式（3）给出．则

2 预估校正算法

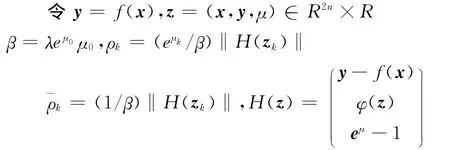
3 收敛性分析

4 数值实验分析

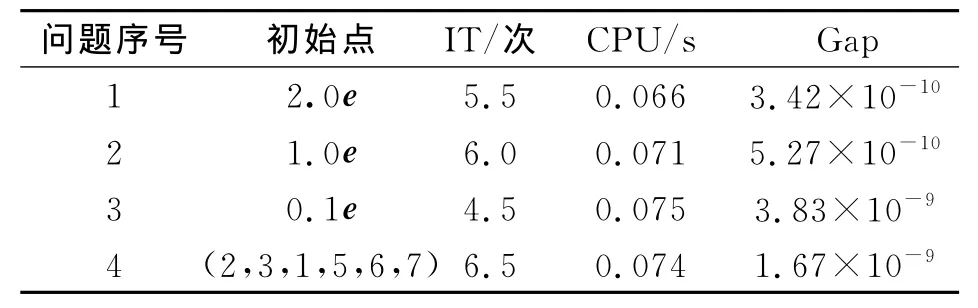
表1 预估校正算法对随机问题的实验结果Tab．1 Numerical results of predictor-corrector algorithm for the random problem

5 结 论

针对单调的二阶锥互补问题，利用对称扰动的FB光滑函数，给出了求解该问题的预估校正算法．与内点算法相比，该算法不依赖于初始点的选取，同时证明了算法在迭代过程中能保证迭代点列在给定的邻域内且不需要额外运算．如果迭代点列满足非奇异假设，则该算法是全局收敛和局部二次收敛的．实验结果表明算法是可行且有效的．

［1］ ALIZADEH F，GOLDFARB D．Second-order Cone Programming［J］．Mathematical Programming，2003，95（1）：3．

［2］ HAYASHI S，YAMASHITA N，FUKUSHIMA M．Robust Nash Equilibria and Second Order Cone Complementarity Problems［J］．Journal of Nonlinear and Convex Analysis，2005，6（2）：283．

［3］ CHEN X，TSENG P．Non-Interior Continuous Methods for Solving Semidefinite Complementarity Problems［J］．Mathematical Programming，2003，95（3）：431．

［4］ HUANG Z H，HAN J Y，CHEN Z W．Predictor-Corrector Smoothing Newton Method Based on a New Smoothing Function for Solving the Nonlinear Complementarity［J］．Journal of Optimization Theory and Applications，2003，117（1）：39．

［5］ SUN D F，SUN J．Strong Semismoothness of Fischer-Burmeister SDC and SOC Complementarity Functions［J］．Mathematical Programming，2005，103（3）：575．

［6］ HUANG Z H，SUN D F，ZHAO G Y．A Smoothing Newton-Vtype Algorithm of Stronger Convergence for the Quadratically Constrained Convex Quadratic Programming［J］．Computational Optimization and Applications，2006，35（2）：199．

［7］ FUKUSHIMA M，LUO Z Q，TSENG P．Smoothing Functions for Second-order Cone Complementarity Problems［J］．SIAM Journal on Optimization，2001，12（2）：436．

［8］ ZHANG X S，LIU S Y，LIU Z H．A Regularization Smoothing Method for Second-order Cone Complementarity Problem ［J］．Nonlinear Analysis：Real World Applications，2011，12（1）：731．