舰载稳定平台PIDNN控制系统设计与仿真＊

薛 航，贾培刚，何思锐，赵绍谚

（西安工业大学 机电工程学院，西安710021）

稳定平台是以自动控制技术、目标识别技术、机电一体化技术为主体，集数据采集及信号处理、微惯性传感器、图像采集与处理、电机运动控制、光学仪器应用等多个学科交叉融合的产物．由于稳定平台能够不断地测量平台姿态的变化，隔离载体的运动，精确保持平台动态姿态的稳定，避免平台上的仪器、设备等随载体的运动而晃动，因此稳定平台被广泛应用于航空航天、导弹火箭、车辆船舶、工业生产和其他的现代化武器装备和民用设施中．文献［1］设计了一种适合于舰船摄像设备的稳定平台，并详细说明了其机械设计结构；文献［2］对常用的稳定平台控制算法模型进行了详尽的描述；文献［3］等在对经典比例积分微分（Proportion Integration Differentiation，PID）控制算法存在的不足进行探讨后，提出了一种神经网络辨识模型的自适应控制算法；文献［4］在一种延时控制系统中使用到了PID神经元网络；文献［5］将PID神经元网络控制算法应用到了伺服系统；文献［6］将PID神经元网络算法进行了控制仿真．

舰船载体在航行过程中不可避免地会受到风浪的影响，造成载体的摇摆，使载体上的数据采集设备难以接收到稳定连续的目标数据，无法实现对采集到的数据进行及时的分析和处理．为了消除舰船载体摇摆所带来的干扰，达到系统所要求的性能指标，需要一套能够有效隔离舰船载体扰动的稳定平台系统．新型舰载三轴稳定平台采用三自由度框架式机械结构，利用惯性测量元件测量台体相对于地理坐标系的位置信息与速度信息，并通过两相步进电机驱动稳定平台的环架运动，使稳定平台能够快速有效地隔离舰船载体扰动，实现平台的随动控制．针对舰载稳定平台的特点以及传统基于速度环和位置环的控制算法的不足，本文以 Microchip PIC24F16KL401单片机为控制核心设计稳定平台伺服控制系统，给出舰载稳定平台控制系统方案．采用PID神经元网络伺服控制算法进行系统控制，分别进行有无外界干扰下系统仿真，得到PID神经元网络控制正弦跟踪位置曲线，分析正弦跟踪位置曲线的稳态误差与跟踪精度，为消除舰船摇摆对目标跟踪精度造成扰动提供理论基础．

1 稳定平台的结构设计

1．1 伺服控制系统的设计

三轴稳定平台采用三自由度框架式结构包括外框、中框和内框三个转动自由度，内框转动轴固定在中框上，中框转动轴固定在外框上，外框转动轴固定在舰体上，内环和中环对应俯仰、偏航运动，外环对应滚转运动，通过控制技术可以实现三自由度稳定平台的常平架作用，使内框的中心运动与载体隔离［3］．根据上述稳定平台的工作原理及舰船载体摇摆干扰的特性，系统的基本设计参数见表1．

该稳定平台伺服控制系统以PIC24F16KL401单片机为控制核心，若平台受到力矩干扰，惯性测量元件就会测量出平台负载的速度信息与位置信息，然后由控制回路经过信息处理和控制算法处理后产生脉冲宽变调制（Pulse Width Modulation，PWM）信号，经电机驱动电路，控制步进电机转动，从而带动平台转轴转动，从而实现稳定跟踪目标的功能．同时为了消除摩擦力矩对电机的影响，在此过程中加入同轴光电编码器反馈电机的实时速度信息给驱动电路，实时调节电机的转速．稳定平台伺服控制系统控制结构如图1所示．

表1 稳定平台系统参数Tab．1 Parameters of stabilized platform

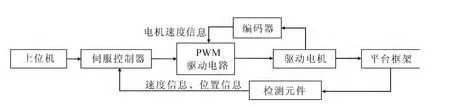
图1 稳定平台伺服控制系统控制结构简图Fig．1 Control structure diagram of stabilized platform servo control system

1．2 稳定平台系统元件的选取

1）驱动电机的选型

作为稳定平台伺服控制系统的执行元件，电机的性能将直接影响到被控对象的运动状况及系统的精度．考虑到稳定平台系统转速较低，转矩较大的特点，为简化系统结构，减低系统干扰，减小误差，在此选用雷赛公司型号为110HS12的两相步进电机，并采取与负载直接耦合的连接方式，通过匹配的驱动器可实现百分之一步级的精确控制．系统选用的步进电机具体参数见表2．／Ω

表2 步进电机参数Tab．2 Parameters of stepper motor

2）惯性器件的确定

稳定平台测量元件是为了能够实时监测稳定平台台体相对于地理坐标系的实际位置信息与速度信息，将数据反馈给伺服控制器，从而保持稳定平台的相对稳定，在此选用XW-IMU5250型（北京星网宇达科技开发有限公司）惯性测量系统．XW-IMU5250采用微机电系统惯性器件的高精度六自由度惯性测量单元，其内部包含三个采用微机械技术加工的角速率陀螺、三个高性能的加速度计和高速数字信号处理电路，可以测量载体在空间中的全方向角度，输出高可靠性的姿态角和航向角，同时可以给出载体的位置、速度信息．

3）电机转速测量元件选取

为了能够实时检测步进电机的速度，在此采用光电编码器作为转速测量工具．光电编码器，是集成光-机-电为一体的数字测角装置，主要以计量光栅为检测元件，通过光电转换将输出轴上的机械角位移量以发光二级管光源为介质通过光栅盘转换成相应的脉冲量，再经计算每秒光电编码器输出脉冲的个数就能反映当前电动机的转速．在此采用SHZSP30XX-001E型（江苏无锡瑞普科技有限公司）绝对式编码器对电机转速进行反馈．

2 PID神经元网络控制算法

2．1 PID神经元网络

基于线性模型被控对象的传统PID控制算法具有结构简单、控制方便、易于实现等特点，而被现代工业控制系统所普遍使用［7］．但对于多耦合、非线性、强扰动、时变系统，想要得到系统的精确模型是很困难的，所以采用传统的PID控制方法就不能达到较好的控制效果．因此，文中考虑采取其他的控制方法，以实现对复杂系统的控制，从而得到较好的系统动态性能，在此我们采用基于神经元网络的新型PID控制算法．

PID 神经元网络（Proportional Integral Deriv-ative Neural Network，PIDNN）是一种多层前向神经元网络，其特点是在神经元网络中融合了PID控制规律，从而使PIDNN中包含了比例、微分、积分的动态处理特性［8］．PIDNN兼具有神经元网络和传统PID控制的优点，无需辨识或者精准测量被控对象的参数和内部结构，能够自适应环境的变化，克服了传统PID控制器在控制非线性随动系统时动态性能较差的缺点，具有较强的鲁棒性．

2．2 PIDNN的结构形式

PIDNN的结构形式随着网络输出量个数的增减而变化，可分为单输出的PIDNN（Single-Output PIDNN，SPIDNN）和多输出的 PIDNN（Multi-Output PIDNN，MPIDNN）．单变量控制系统适用SPIDNN，多变量控制系统适用 MPIDNN，其中SPIDNN是PIDNN的基本形式，多个子网交叉并联的SPIDNN构成了MPIDNN．

SPIDNN与一般的神经元网络结构类似，是三层前向网络，即输入层、隐含层、输出层，采用 结构，不同的是一般的神经元隐含层都是静态的，而SPIDNN的隐含层分别定义了比例元，微分元和积分元，用于实现PID运算，是动态的．而MPIDNN则是SPIDNN的扩充和发展形式，其结构形式如图2所示．图2中P为放大系数，I为积分系数，D为微分系数．

如果被控系统有n个输入和m个输出，则该MPIDNN是由n个SPIDNN交叉并联构成，结构形式为2n×3n×m．2n个神经元构成了网络的输入层，3n个神经元处理单元（包括n个比例元，n个积分元，n个微分元）构成了网络的隐含层，m个神经元构成了网络的输出层．输入层至隐含层按子网独立，隐含层至输出层的连接权相互交叉连接，从而使得MPIDNN结合为统一的整体．

由于该舰载稳定平台系统是典型的多耦合、非线性、强扰动、时变系统，在此采用MPIDNN控制算法，并结合牛顿梯度法调节PIDNN的权值［9］．

图2 MPIDNN结构形式简图Fig．2 Structure diagram of multi-output PIDNN

2．3 稳定平台的PIDNN控制结构

由图1的稳定平台伺服控制系统的控制结构简图，可得到基于PIDNN稳定平台伺服控制系统，如图3所示．图3中θ0为输入角，θ1为输出角，KPWM为放大系数，TS为PWM装置的延迟时间，Ra为电枢绕组电阻，T1为电机的电磁时间常数，Ce为电机反电势系数，Kf为电机速度反馈常数，Wd表示摩擦力矩干扰，s为复变量．通过系统结构的近似处理和结构图的等效变换原则及动态跟随性能与频域指标的关系，可知系统的传递函数为

式 中：τn＝Tm＝ 0．487 2；KPWM＝ 2；T1＝0．001 6；Ra＝0．37Ω；Ce＝0．24V·s·rad-1；Kf＝0．4V·min-1．

图3 稳定平台PIDNN控制结构图Fig．3 Control structure diagram of PIDNN of stabilized platform

3 控制系统仿真

设定输入层至隐含层比例元和微分元连接权值初值为

输入层至隐含层积分元连接权值初值为

隐含层至输出层连接权值初值为

式中：wsij为各子网输入层至其对应隐含层的连接权值；w′sjh为隐含层至输出层的连接权值；s为子网的序号，s＝1，2，3；i为子网输入层的序号，i＝1，2，3；j为子网中隐含层神经元的序号，j＝1，2；h为输出层神经元的序号，h＝1，2，3．

采用批学习方法，每批为100个采样点，步长为0．1，则目标函数为

式中：yp（k）为实际输出；rp（k）为理想输出；p为系统被控变量的序号．

若只考虑基波对系统的影响，舰船的运动可按正弦信号处理，因此取期望指令信号为正弦信号r＝0．5sin6π，采样时间为1ms，仿真结果如图4～5所示．

从图4看出，采用PIDNN控制算法的稳定平台系统具有良好的跟踪精度，对外部的干扰拥有很好的抑制作用，有效地降低了被控对象的非线性影响．图5给出了稳定平台系统的误差角度特性曲线，从图5可以看出系统具有较高的动态性能，且最大稳态误差小于0．001rad，能够很好的保证系统的稳定，使系统具有较好的自适应性和鲁棒性．

图4 稳定平台PIDNN控制正弦跟踪曲线Fig．4 Sine tracking curve of PIDNN control of stabilized platform

图5 稳定平台PIDNN控制正弦跟踪位置误差曲线Fig．5 Sine tracking error curve of PIDNN control of stabilized platform

图6 零输入加入干扰的PIDNN控制正弦跟踪位置曲线Fig．6 Sine tracking curve of zero input PIDNN control with disturbance

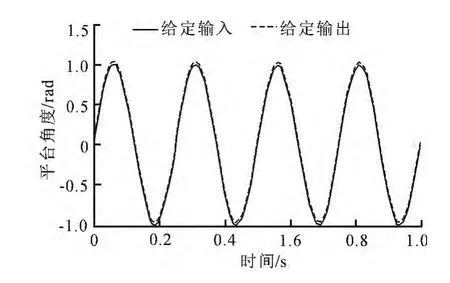
图7 加入干扰的PIDNN控制正弦跟踪位置曲线Fig．7 Sine tracking curve of PIDNN control with disturbance

从图6上可以看出，在加入摩擦力矩干扰与载体扰动干扰后，PIDNN控制仍然具有较好的跟踪精度，系统的误差在-0．05～＋0．05rad范围内波动．图7表明，在加入摩擦力矩干扰与扰动干扰后，PIDNN系统响应跟踪仍然保持着较小误差．

4 结 论

1）PIDNN稳定平台控制系统结构简单，系统模型不精确性适应性强，实现了自我学习和自适应能力，被控对象非线性干扰得以克服，系统稳定．

2）仿真结果表明该控制系统的误差在-0．05～＋0．05rad范围内波动，跟踪精度较传统PID提高．在加入摩擦力矩干扰与扰动干扰后，PIDNN系统的响应跟踪误差仍然较小，自适应性和鲁棒性增强，有效隔离了载体对数据采集设备的影响．

［1］ 张鹏．舰载摄像稳定平台的结构设计［J］．舰船电子对抗，2006，29 （3）：70．ZHANG Peng．Structural Design of Shipboard Shooting Stabilized Platform［J］．Shipboard Electronic Countermeasure，2006，29（3）：70．（in Chinese）

［2］ 张平，董小萌，付奎生，等．机载／弾载视觉导引稳定平台的建模与控制［M］．北京：国防工业出版社，2011．ZHANG Ping，DONG Xiao-meng，FU Kui-sheng，et al．Modeling and Control of Airbore／Missile-Borne Vision Guidance Stabilized Platform［M］．Beijing：National Defense Industry Press，2011．（in Chinese）

［3］ 沈晓洋，陈洪亮，刘昇．机载陀螺稳定平台控制算法［J］．电光与控制，2011，18（4）：46．SHEN Xiao-yang，CHEN Hong-liang，LIU Sheng．A Control Algorithm for Airborne Gyro-Stabilized Plat-form［J］．Electronics Optics ＆ Control，2011，18（4）：46．（in Chinese）

［4］ SHU H L，YOU G．PID Netural Networks for Time-Delay Systems［J］．Computer ＆ Chemical Engineering，2000，7 （4）：859．

［5］ 张洪亮，王志胜．基于PID神经元网络的稳定平台伺服控制系统设计［J］．电工电气，2011，16（1）：17．ZHANG Hong-liang，WANG Zhi-sheng．Stable Platform Servo Control System Design Based on PID Neural Network［J］．Electrical ＆ Electronics，2011，16 （1）：17．（in Chinese）

［6］ 曾军，方厚辉．神经网络PID控制及其 Matlab仿真［J］．现代电子技术，2004，169（2）：51．ZENG Jun，FANG Hou-hui．Neural Network PID Controller and Its Matlab Simulation［J］．Modern Electronics Technique，2004，169（2）：51．（in Chinese）

［7］ MCAREE P R，DANIEL R W．A Fast Robust Solution to the Stewart Platform Forward Kinematics［J］．Robotic Systems，1996，8 （13）：407．

［8］ 杨蒲，李奇．三轴陀螺稳定平台控制系统设计与实现［J］．中国惯性技术学报，2007，15（2）：172．YANG Pu，LI Qi．Design and Realization of Control System for Three Axis Gyro Stabilized Platform［J］．Journal of Chinese Inertial Technology，2007，15（2）：172．（in Chinese）

［9］ 舒怀林．PID神经元网络及其控制系统［M］．北京：国防工业出版社，2006．SHU Huai-lin．The Control System of PID Neural Network［M］．Beijing：National Defense Industry Press，2006．（in Chinese）