中国低碳经济发展的空间非均衡及动态演进

黄 杰，贾登勋

（兰州大学 经济学院，甘肃 兰州730000）

一、引 言

伴随着经济的增长，全球面临的能源、环境和气候变化的挑战越来越严峻，经济发展的低碳化已成为国际共识。二氧化碳排放量的剧增使中国面临巨大的国际减排压力，本着对国民及国际社会负责任的态度，中国政府于2009年哥本哈根气候大会前夕，提出到2020年中国的单位GDP二氧化碳排放量比2005年下降40%～45%的自主减排行动目标，这是中国统筹国内可持续发展和应对全球气候变化所做的战略选择。为实现减排目标，中国政府将其纳入国家长期发展战略中，在“十二五”规划中提出到2015年单位GDP二氧化碳排放量（即碳强度）要比2010年下降17%的约束性目标。在全球大力推进二氧化碳减排的背景下，还应认识到中国仍处于工业化和城市化加速发展的关键阶段，发展经济仍是这一阶段的重中之重，即二氧化碳减排必须在保证经济增长的前提下进行，以实现经济发展与二氧化碳减排的共赢。

二、文献回顾

目前关于低碳经济发展的衡量多采用多指标的综合效率评估。DEA 模型（Data envelopment analysis）的出现为效率测度提供了一个很好的工具，然而与传统的效率测度不同，低碳经济发展效率的测度不但要考虑 “好”的产出（GDP），还必须考虑二氧化碳这种“坏”的产出。在处理“坏”产出，即非期望产出（二氧化碳排放）的过程中，由于所选择的方法和具体模型的不同，可以分为以下几种处理方法。1．Hailu和杜克锐等在对效率进行测度时把非期望产出（二氧化碳排放）作为投入要素纳入到模型中进行分析［1－2］。2．曹珂等采用乘法逆转法对非期望产出进行转换，使其在形式上满足模型要求［3］。然而王兵等指出，将二氧化碳作为投入要素或是做线性变换使其成为期望产出，这两种处理方法不仅有悖于实际的生产过程，还可能会破坏模型的凸性要求［4］。3．Watanabe、胡鞍钢和张进铭等采用Chung等提出的方向性距离函数，通过方向向量设置，将二氧化碳排放作为非期望产出来进行处理的方法［5－8］。但Fukuyama等研究发现，使用方向性距离函数在进行效率测度时无法剔除投入产出松弛造成的非效率成分，将导致估计出的效率值偏高［9］。4．Toshiyuki Sueyoshi、Yongrok Choi和周五七等采用Tone等提出的基于非径向、非角度包含非期望产出的SBM（Slacks－based Model）模型进行效率测度［10－12］。这种模型不仅考虑了投入产出变量的松弛问题，又同时考虑了产出中的非期望产出问题，在包含非期望产出的效率测度模型中逐渐被人们认可。

目前关于空间非均衡的研究多采用指标法，如用变异系数、泰尔指数和基尼系数等指标来衡量研究对象的空间非均衡程度。由于变异系数不能分解，无法衡量组内差距与组间差距对整体差距的贡献，因此越来越多的人开始采用泰尔指数对空间非均衡问题进行研究，进而对空间非均衡的来源进行分解。如胡志远等利用泰尔指数及其分解方法对江苏省1987—2004年的人均GDP、人均农业生产总值、人均城乡居民储蓄存款和人均社会商品零售总额四个指标的区域差异进行了测度，研究发现除人均农业生产总值外，江苏省三大区域之间的差异程度呈逐步扩大之势［13］。干春晖等利用泰尔指数及其分解方法从产业角度对中国地区间经济差距进行分析，研究认为产业内差距是区域经济差距产生的主要原因［14］。但是Dagum指出，利用泰尔指数在测度不同组别之间的非均衡时，要求不同组别之间的样本要满足独立同方差且属于正态分布，在分解时仅仅考虑了子样本的不同，而没有考虑子样本的分布状况［15－16］。为解决上述问题，Dagum提出了一种新的基尼系数分解方法，即按子群方法对基尼系数进行分解，将空间非均衡分解为区域内差距、区域间净值差距和超变密度三个部分，不仅克服了上述方法的不足，还有效地解决了空间非均衡的来源问题。

综上所述，为保证本研究的科学性和准确度，本文选择基于非径向、非角度包含非期望产出的SBM模型作为测度工具，利用中国30个省份（由于西藏缺少数据较多，故本文未把西藏列入研究对象）2000—2012年的数据，测度中国各省域的低碳经济发展效率；进而利用Dagum基尼系数及按子群分解方法来测度低碳经济发展的空间非均衡程度，并按照东部、中部和西部三大区域进行分解，从而揭示出中国三大区域低碳经济发展的空间非均衡来源及构成；最后通过Kernel密度函数曲线对中国整体及三大区域低碳经济发展的动态演进趋势进行分析，并提出缓解中国区域低碳经济非均衡发展的对策建议。

三、研究方法和样本数据

（一）研究方法

1．基于非径向、非角度包含非期望产出的SBM模型

DEA模型已成为目前效率测度的主要分析工具。然而Tone等研究发现，传统的DEA模型主要是采用径向的和角度的度量方法，没有考虑存在投入过度或产出不足的现实情况，从而造成测量的结果产生偏差。于是Tone先后提出了基于非径向和非角度的SBM模型和加入非期望产出的SBM模型，前者考虑了投入产出变量的松弛问题，后者在前者的基础上又考虑了产出中的非期望产出问题［17－18］。本文根据Tone提出的基于非径向、非角度包含非期望产出的SBM理论模型，借鉴F re等对环境生产技术的研究以及Zhou等等构建的环境绩效测量模型，首先构造一个包含投入、期望产出和非期望产出的生产可能集T［19－21］。在生产可能集中资本存量（k）、劳动力人数（l）和能源消费总量（e）为投入变量；GDP（g）为期望产出，二氧化碳排放总量（c）为非期望产出，生产可能集可描述为：T＝｛（k，l，e，g，c）∶ （k，l，e）can produce（g，c）｝，本 文 的生产可能集T满足闭合、有界和凸性的特征，且投入要素和期望产出满足强可处置性①①要素可处置性是指在生产过程中要素能不受限制地增加或减少。特征。同时根据F re等环境生产技术需要满足非期望产出的弱可处置性，即如果（k，l，e，g，c）∈T且0≤θ≤1，则（k，l，e，θg，θc）∈T；以及期望产出与非期望产出的“零和”（Null Joint）特征①①“零和”特征指在生产系统中期望产出的存在必然伴随着非期望产出。，即如果（k，l，e，g，c）∈T且c＝0则g＝0［21］。据此，本文的SBM模型可以表示为式（1）：

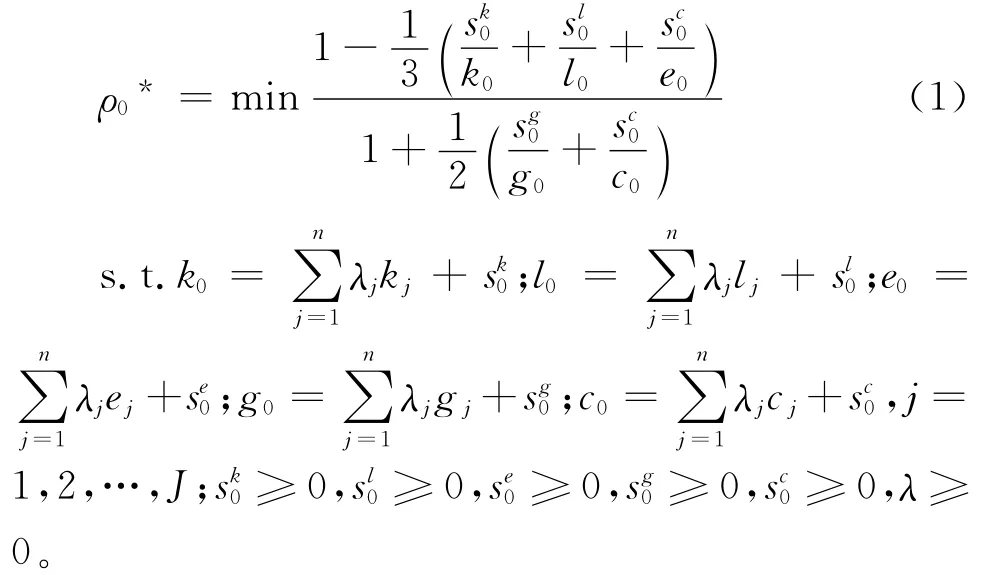
在模型（1）中，下标0表示效率估计中所观测到变量的量，下标j为观测变量序号，约束条件中的是一个非负的权重向量，如果，则表示上述DEA模型为规模报酬不变模型分别为资本存量、劳动力人数、能源消费总量、GDP和二氧化碳排放总量的松弛变量。此时，如果，且松弛变量时，决策单元DUM（Decision Making Units）是有效率的；否则该决策单元是无效率的，此时可以通过调 整松弛变量进行效率改进。

根据Tone文中的方法，将非线性规划模型（1）转换为可求解的线性规划模型（2）进行求解：

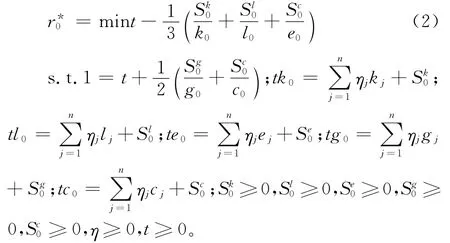
在模型（2）中，满足，通过线性规划得到最优解（），进而得到决策单元的效率值。

2016年8月22日，习近平总书记视察青海首站走进盐湖，听取盐湖资源开发和循环经济汇报，充分肯定了“走出钾、抓住镁、发展锂、整合碱、优化氯”战略布局，要求稳扎稳打，有序推进。习近平总书记视察盐湖增强了盐湖人的信心，坚定了盐湖人的信念，鼓舞了盐湖人的士气，激发了盐湖人强创新、强管理、强党建的干劲。六十一甲子，辉煌再启程！

2．Dagum基尼系数及按子群分解方法

为避免泰尔指数在差异分解过程中过强的前提假设，以及传统基尼系数不能分解的问题，Dagum提出了按子群对基尼系数进行分解的方法，按照Dagum的分解方法，可将总体基尼系数G分解为区域内差距的贡献Gw，区域间净值差距的贡献Gnb和超变密度②②超变密度是 Dagum（1960）在《Teoria de la transvaloración，sus aplicaciones a la economía》一文中提出，即两个不同的区域之间，经济发展较差的那个区域中存在着比较富裕的个体，而经济发展较好的区域中存在着相对贫穷的个体，由这两个部分共同存在所导致的区域差距被称为超变密度。（Intensity of Transvariattion）的贡献Gt三个部分，且满足G＝Gw＋Gnb＋Gt。公式如式（3）所示，其中n是全国的省份个数，k是区域划分的个数，在本文中k＝3；j和h分别表示k个区域中的不同区域且j、h＝1，2，…，k；nj和nh分别表示j和h区域内的省份个数；yji表示j区域内第i个省份的低碳经济发展效率，yhr表示h区域内第r个省份的低碳经济发展效率，为全国低碳经济发展效率的均值。公式（4）、（5）分别表示各区域的区域内基尼系数Gjj和区域内差距的贡献Gw；公式（6）、（7）分别表示地区间基尼系数Gjh和地区间净值差距的贡献Gnb；公式（8）表示超变密度的贡献Gt。

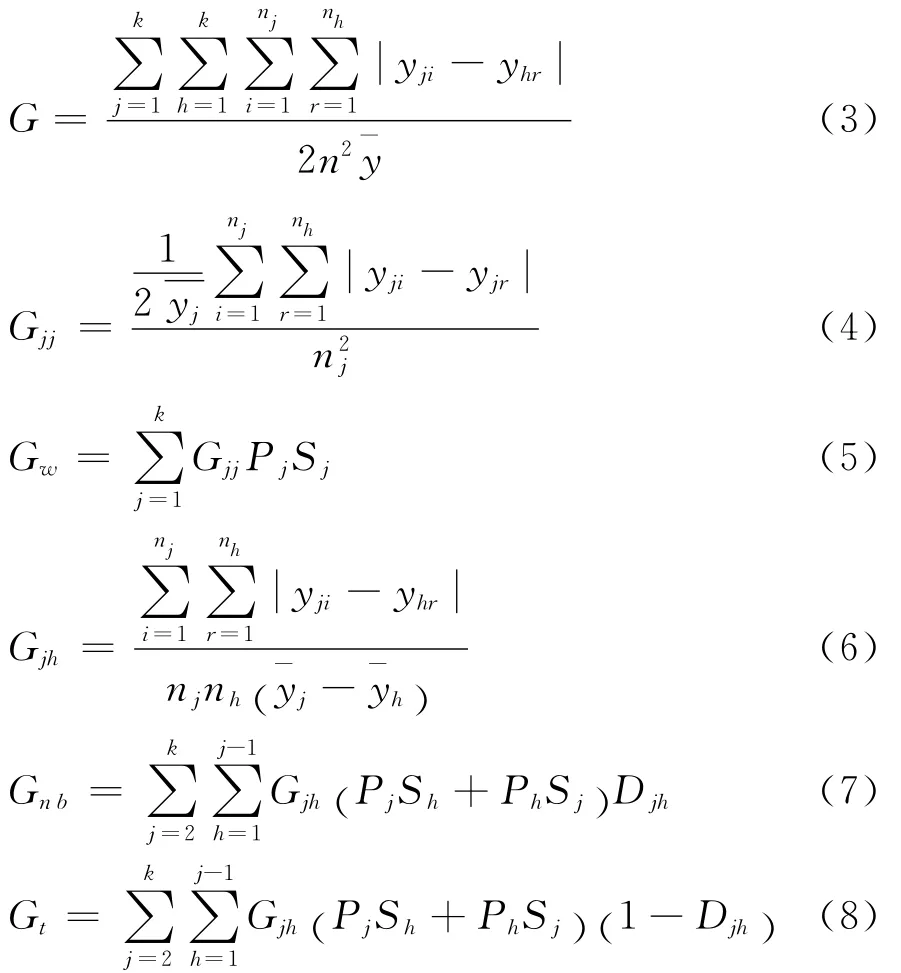
为方便计算，在进行区域划分时，要按照低碳经济发展效率均值的升序对区域进行排序，使之满足，其中，为j区域中所包含的省份占全部考察省份的份额为j区域低碳经济发展效率之和与总的低碳经济发展效率之比，且满足；D为j和h区域间低碳经济jh发展效率相对比值，定义如公式（9）所示。其中，djh和Pjh的计算分别如公式（10）、（11）所示，其中Fj（x）和Fh（x）分别为j和h区域的累积分布密度函数。我们将djh定义为区域间空间非均衡贡献率的差值，即j和h区域中yji－yhr＞0的所有样本值之和的数学期望，Pjh定义为超变一阶矩，即j和h区域中yhr－yji＞0的所有样本值之和的数学期望。

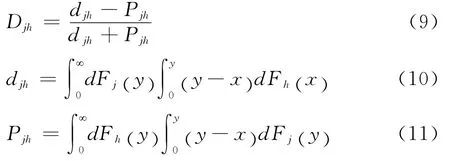
3．Kernel密度估计

核密度估计（Kernel Density Estimation）作为一种对随机变量的概率密度进行估计的非参数方法，可以通过连续的密度函数曲线对随机变量的分布形态进行描述。假设x1，x2，…，xn为来自连续总体X的样本，在任一点x处的总体密度函数为f（x）的核密度估计可以定义为式（12）：

其中K（·）称为核函数（kernel function），h为带宽。为保证作为密度函数估计的合理性，要求核函数满足，即要求核函数K（·）是某个分布的密度函数。常用的核密度函数有三角核函数（Triangle）、四角核函数（Quaritic）、高斯核函数（Gaussian）和Epanechnikov核函数等。基于一般化的考虑，本文选择随机变量x服从正态分布的高斯核函数①①Smola A．J．（1998）认为在缺少过程的先验知识时，选择高斯核函数较其它核函数好。如式（13）：

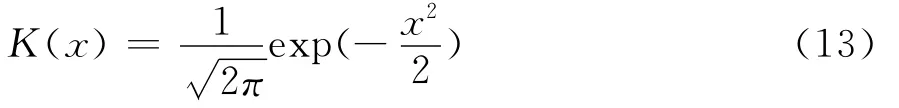
Silverman等研究发现，核密度函数在估计中对带宽h的选择非常敏感，带宽较大时，核密度估计的方差较小，密度函数曲线越平滑，但此时过于平滑的曲线会掩盖数据本身的特征，核密度估计效果较差；带宽较小时，核密度估计的方差会变大，密度函数曲线不够平滑，此时难以排除随机误差产生的噪音，但估计精度会提高。因此，在实践中要根据样本的特征，尽可能选择较小的带宽，把h作为n的函数进行带宽选择，使h（n）满足：当n→ ∞，h＝h（n）→0。

（二）数据来源及处理

本文资本投入利用张军等所采用的“永续盘存法”计算出数据，并以2000年为基期估算出各省份2000～2012年的资本存量，基础数据来源于历年《中国统计年鉴》；劳动力人数采用各地区年底从业人员总数表示，数据来源于历年《中国人口与就业统计年鉴》；能源投入用各省份能源消费总量表示，数据来源于历年《中国能源统计年鉴》；期望产出用各省份以2000年不变价格计算的实际GDP表示，基础数据来源于历年《中国统计年鉴》；非期望产出二氧化碳排放量的测算，由于中国并没有直接监测数据，本文是基于《中国能源统计年鉴》和IPCC2006年给出的各种能源燃烧的平均低位发热量、碳排放系数和氧化系数来估算各省份的CO2排放量②②由于篇幅有限，各地区二氧化碳排放数据不再罗列，如有需要可向作者索取。，计算公式如式（14）：

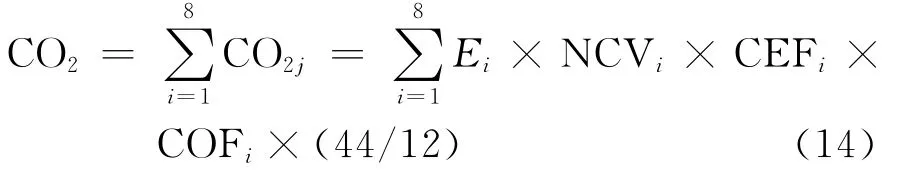
其中，CO2表示估算的二氧化碳排放量，i表示各种化石燃料，E代表初级化石燃料的消耗量，NCV为能源的平均低位发热量，CEF为碳排放系数，COF为能源的氧化系数。本文所选取的能源是指煤炭、焦炭、原油、燃料油、汽油、煤油、柴油和天然气。

四、中国低碳经济发展效率及其空间非均衡特征

首先，利用非径向、非角度包含非期望产出的SBM模型测度了中国30个省份2000—2012年的低碳经济发展效率，如表1。从表1中可以看出：第一，在样本考察期内中国低碳经济发展的整体效率均值呈逐渐上升之势，若以2000年为基期，到2012年中国低碳经济发展的整体效率均值年均上升0．21%，中部和西部地区的低碳经济发展整体效率均值年均上升1．06%和0．31%，而东部地区的低碳经济发展整体效率均值年均下降0．36%，东部地区的整体效率均值的下降主要是由于河北、辽宁、山东和海南四省的低碳经济发展效率下降引起。第二，中国低碳经济发展较好的地区主要位于经济发展水平较高的东部地区，中西部地区的低碳经济发展效率虽有所上升，但整体水平仍远低于东部地区，西部地区的低碳经济发展不仅低于东部地区，且目前只有全国平均水平的70%左右。

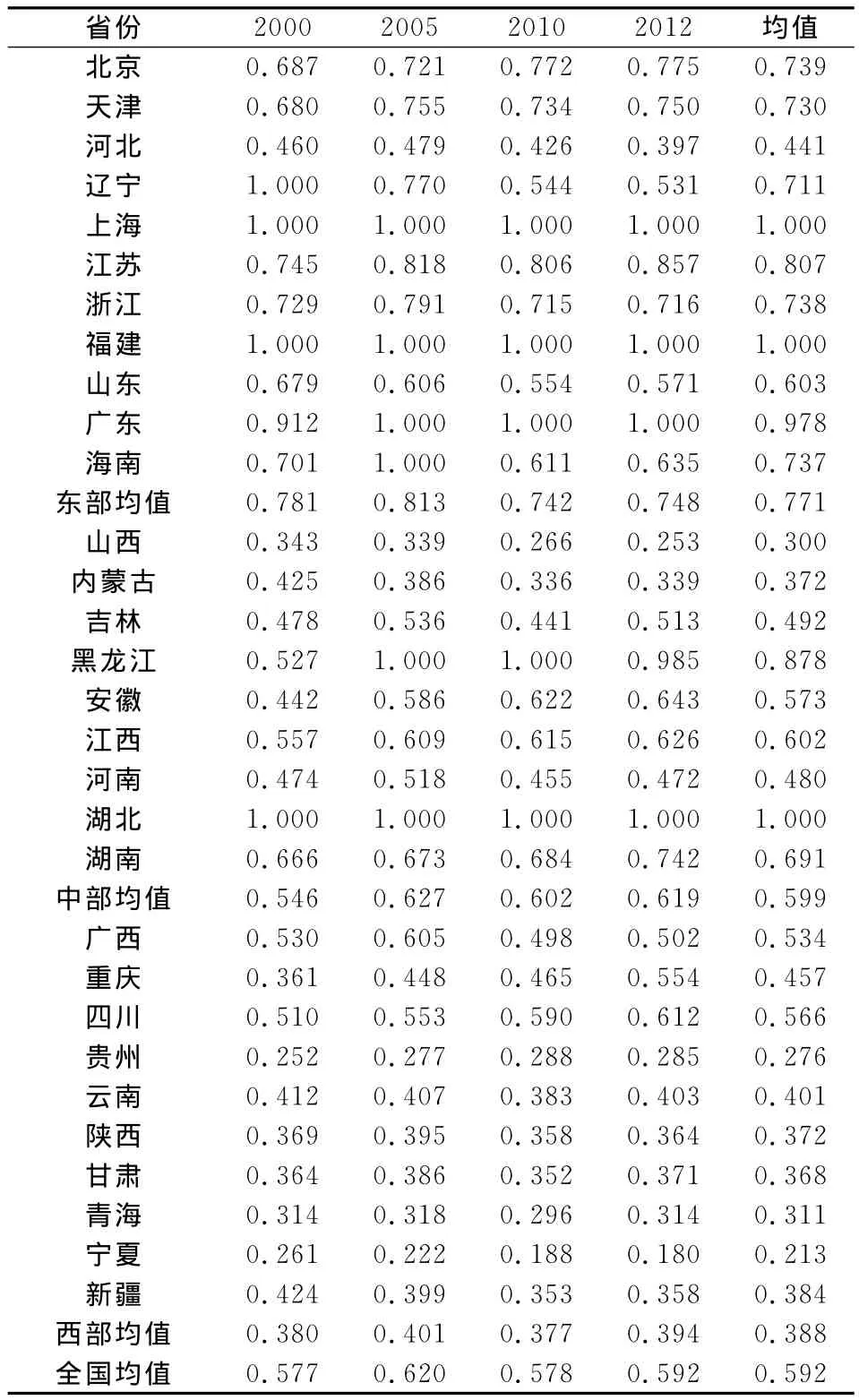
表1 部分年份的各省份低碳经济发展效率

其次，利用ArcGis软件绘制了中国2000年和2012年各地区低碳经济发展效率的空间分布图。从图1和图2中可以清晰地看出，中国的低碳经济发展表现出明显的空间非均衡特征。从空间上看，东部沿海地区的低碳经济发展效率较高，有些省份达到了最优效率，即效率值为1，中部次之，而西部地区的低碳经济发展效率最低，除广西和四川外，其余省份的效率值都均在0．5以下。从时间来说，从2000年到2012年，中国整体的低碳经济发展效率在提高，但西部地区的低碳经济发展效率除广西、重庆、四川和贵州外，其余省份却在下降，而东、中部地区的大部分省份的低碳经济发展效率都在上升。总体而言，中国低碳经济发展的空间非均衡程度随着时间的推移有加剧之势。

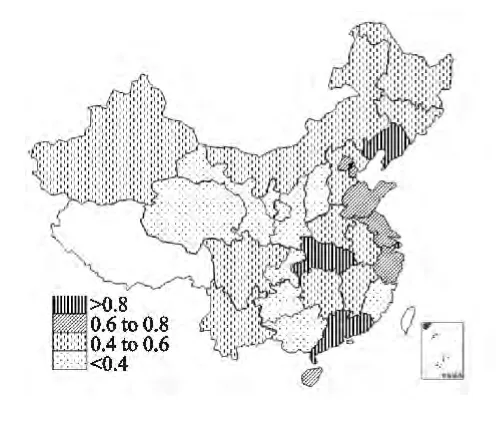
图1 中国低碳经济发展效率地区分布（2000年）

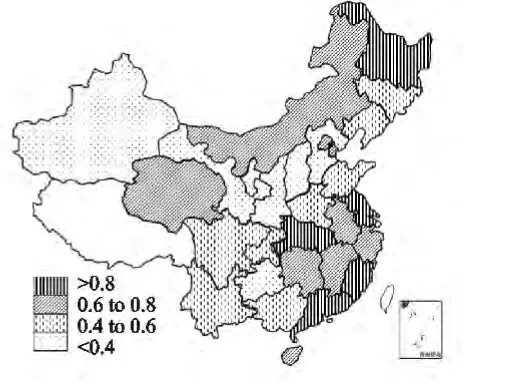
图2 中国低碳经济发展效率地区分布（2012年）

五、中国低碳经济发展空间非均衡程度的测度及分解

（一）从整体层面考察

表2报告了中国低碳经济发展的空间非均衡的测度结果，从结果来看，中国的低碳经济发展的空间非均衡程度在不断加深，在样本考察期内只有2002年和2003年两年的总体基尼系数出现轻微的下降，其余年份都在缓慢上升，并于2012年达到最大值0．234。若以2000年为基期，到2012年中国低碳经济发展的整体空间非均衡程度年均上升0．71%，若以2005年为基期，2012年中国低碳经济发展的整体空间非均衡程度年均上升0．95%。

（二）区域内空间非均衡程度及其演变趋势

如表2所示，在样本考察期内，东部和中部的区域内空间非均衡程度在加剧，西部地区的空间非均衡程度从高到低逐渐趋于稳定。具体来说，中部地区的空间非均衡程度最深，从2000年的0．164一直上升到2012年的0．232；西部地区的空间非均衡程度变动较小；东部地区的空间非均衡程度虽然变动不大，但可以明显地分为两个阶段：第一阶段为2000—2006年，该阶段的地区空间非均衡程度维持在0．11左右，第二阶段从2007年开始，低碳经济发展效率的空间非均衡程度稳定在0．14左右。若以2000年为基期，东、中和西三大区域的低碳经济发展空间非均衡程度年均上升1．8%、2．9%和1．7%，若以2005年为基期，东、中和西三大区域的低碳经济发展空间非均衡程度则年均上升3．4%、2．7%和0．8%。

（三）区域间的空间非均衡程度及其演变趋势

从表2来看，在样本考察期内，中国东部与中部地区之间的空间非均衡程度，先由2000年的0．22下降到2002年的最小值0．188，之后又逐渐上升到2012年0．21，东部与西部地区之间的空间非均衡程度则小幅波动，2012年的区域间基尼系数仍为0．334，而中、西部之间的空间非均衡程度在持续扩大，由2000年的0．183上升到2012年0．259。若以2000年为基期，则东部和中、西部之间的空间非均衡程度年均下降0．39%和0．34%，中部与西部之间的空间非均衡程度则年均上升3%；若以2005年为基期，则东部和中部之间的空间非均衡年均上升1．1%，东部和西部之间的空间非均衡程度年均下降0．35%，中部与西部之间的空间非均衡程度年均上升1．4%。

表2 中国低碳经济发展效率的基尼系数及分解

（四）区域非均衡的来源及贡献

中国低碳经济发展的区域间空间非均衡程度在不断下降，而区域内空间非均衡程度在上升，超变密度则一直都是中国低碳经济发展空间非均衡问题的主要来源。具体来说，区域间的空间非均衡程度对整体空间非均衡程度的贡献率从2000年的39．6%下降到2012年的32．2%；而区域内空间非均衡程度对整体空间非均衡程度的贡献率则从2000年的20．7%上升到2012年的24．8%；同时超变密度的贡献率从2000年的39．7%上升到2012年的42．9%，成为中国低碳经济发展的空间非均衡程度的主要来源。若以2000年为基期，则区域间空间非均衡程度对整体非均衡程度的贡献率年均下降1．71%，区域内的贡献率年均上升1．53%，超变密度的贡献率则年均上升0．66%；若以2005年为基期，则区域间的空间非均衡程度对整体非均衡程度的贡献率年均下降0．72%，区域内的贡献率年均上升1．71%，超变密度的贡献率则年均下降0．36%。

六、中国低碳经济发展空间非均衡的分布动态演进

（一）全国低碳经济发展的核密度估计

图3为中国及三大区域基于高斯核函数的核密度估计图。从全国层面看，如图3a所示，与2000年相比，2003、2005、2007、2010和2012年中国各省份的低碳经济发展核密度估计曲线的波峰在不断下降且逐步右移，这说明中国的低碳经济发展随着时间的推移，空间非均衡程度在逐渐加深。新波峰的出现说明中国低碳经济发展逐渐呈两极化趋势。

（二）三大区域的低碳经济发展核密度估计

从图3b上看，与2000年相比其余各年曲线逐渐变得扁而宽，这说明东部地区的低碳经济发展空间非均衡程度在变大。2000、2003、2005、2007年均表现出两极化趋势，但第二个波峰越来越低，到了2010和2012年时，波峰逐渐由两个变为一个，这说明虽然东部地区内的低碳经济发展差距在逐步扩大，但东部地区的低碳经济发展已从以前的两极分化发展，改善为均衡前进的发展模式。从图3c上看，在样本考察期内，密度函数曲线中心逐渐向右偏移，双峰趋势得到加强，且宽度在拉大，这说明中部地区的低碳经济发展空间非均衡程度在加大，且存在明显的两极分化现象。从图3d上看，2003、2005和2007年的波峰，尤其是2010和2012年的波峰明显低于2000年的波峰，且有新的波峰隐现。这说明中国西部地区的低碳经济发展空间非均衡程度在加深，且存在多极化趋势。

图3 低碳经济发展效率的Kernel密度估计

七、结论与建议

通过对中国低碳经济发展空间非均衡程度的测量及其演进趋势的分析，得到如下结论：第一，观察利用ArcGis绘制的空间分布图，可以看出中国的低碳经济发展显示出显著的空间非均衡特征。第二，Dagum基尼系数分解结果表明，中国的低碳经济发展的空间非均衡程度一直在上升，三大区域内的空间非均衡程度和中部西部之间的空间非均衡程度也在逐渐加大，但东部和中部、东部和西部之间的空间非均衡程度略有下降；中国低碳经济发展的空间非均衡主要来源于区域间的非均衡和超变密度两个部分，这两部分2012年的贡献率虽较2000年的79．31%有所下降，但仍较高达75．16%。第三，Kernel密度估计显示，中国整体和东、中和西三个部分的低碳经济发展效率在不断提高，但空间非均衡程度呈逐渐加剧之势。

由于中国各个地区所处的发展阶段和拥有的资源禀赋不同，改善中国低碳经济发展的空间非均衡状况应根据每个地区的实际情况制定不同的低碳经济发展策略。第一，强化优势地区低碳经济发展水平。低碳经济发展水平较高的地区主要分布在东部沿海和中部一些工业基础较好的地区，我们应积极强化优势地区的低碳经济发展水平，实现以点带面、优势地区带动落后地区，逐步加快中国整体的低碳经济发展水平。第二，提高落后地区低碳经济发展水平。中国低碳经济发展水平较低的地区主要集中在广大的西部地区和一些煤炭资源较为丰富的中部地区，要从技术层面和经济层面给予低碳发展落后地区更多、更大的支持。第三，加强区域间低碳发展的交流与合作。这样做一方面有利于低碳技术的扩散，落后地区可以通过市场手段引进先进的低碳技术以降低本地的碳排放，提高本地的低碳发展水平；另一方面，区域间的合作有利于提高落后地区的经济发展水平，缩小区域间的低碳发展差距，进而降低中国低碳经济发展的整体空间非均衡程度。

［1］ Hailu A，Veeman T S．Alternative Methods for Environmentally Adjusted Productivity Analysis ［J］．Agricultural Economics，2001，25（2／3）．

［2］ 杜克锐，邹楚沅．我国碳排放效率地区差异、影响因素及收敛性分析——基于随机前沿模型和面板单位根的实证研究［J］．浙江社会科学，2011（11）．

［3］ 曹珂，屈小娥．中国区域碳排放绩效评估及减碳潜力研究［J］．中国人口·资源与环境，2014，24（8）．

［4］ 王兵，朱宁．不良贷款约束下的中国银行业全要素生产率增长研究［J］．经济研究，2011（5）．

［5］Watanabe M，Tanaka K．Efficiency Analysis of Chinese Industry：A Directional Distance Function Approach ［J］．Energy Policy，2007，35（12）．

［6］ 胡鞍钢，郑京海，高宇宁，等．考虑环境因素的省级技术效率排名（1999—2005）［J］．经济学（季刊），2008（3）．

［7］ 张进铭，廖鹏．中国省际全要素能源效率变动分解——基于环境约束条件下的研究［J］．统计与信息论坛，2012，27（3）．

［8］ Chung Y H，F re R，Grosskopf S．Productivity and Undesirable Outputs：A Directional Distance Function Approach［J］．Journal of Environmental Management，1997，51（3）．

［9］ Fukuyama H，Weber W L．A Directional Slacks－based Measure of Technical Inefficiency ［J］．Socio－Economic Planning Sciences，2009，43（4）．

［10］Sueyoshi T，Goto M．A Combined Use of DEA （Data Envelopment Analysis）with Strong Complementary Slackness Condition and DEA－DA（Discriminant Analysis）［J］．Applied Mathematics Letters，2011，24（7）．

［11］Choi Y，Zhang N，Zhou P．Efficiency and Abatement Costs of Energy－related CO2Emissions in China：A Slacks－based Efficiency Measure［J］．Applied Energy，2012，98（10）．

［12］周五七，聂鸣．中国工业碳排放效率的区域差异研究——基于非参数前沿的实证分析［J］．数量经济技术经济研究，2012（9）．

［13］胡志远，欧向军．基于泰尔指数的江苏省区域差异多指标测度［J］．经济地理，2007（5）．

［14］干春晖，郑若谷．中国地区经济差距演变及其产业分解［J］．中国工业经济，2010（6）．

［15］Dagum C．A New Approach to the Decomposition of the Gini Income Inequality Ratio［J］．Empirical Economics，1997（4）．

［16］Dagum C．Decomposition and Interpretation of Gini and the Generalized Entropy Inequality Measures［J］．Statistica－Bologna，1997，57（1）．

［17］Tone K．A Slacks－based Measure of Efficiency in Data Envelopment Analysis［J］．European Journal of Operational Research，2001，130（3）．

［18］Tone K．Dealing with Undesirable Outputs in DEA－A Slacks－based Measure（SBM）Approach［C］．Presentation at NAPW III，Toronto，2004．

［19］F re R，Grosskopf S，Pasurka C A．Environmental Production Functions and Environmental Directional Distance Functions［J］．Energy，2007，32（7）．

［20］Zhou P，Ang B W，Poh K L．Slacks－based Efficiency Measures for Modeling Environmental Performance［J］．Ecological Economics，2006，60（1）．

［21］Rolf Fare S G C A．Multilateral Productivity Comparisons When Some Outputs are Undesirable：A Nonparametric Approach［J］．The Review of Economics and Statistics，1989，71（1）．