超大型集装箱船的结构设计
2015-01-01王伟飞
韩 钰,陈 磊,王伟飞,虞 赉
(中国船舶及海洋工程设计研究院,上海 200011)
0 引 言
随着达飞的16000TEU和马士基的18000TEU超大型集装箱船的连续交付运营,超大型集装箱船(通常指船长>350m的集装箱船Ultra Large Container Ship,(ULCS))近年逐渐成为热门船型。中国船舶及海洋工程设计研究院(MARIC)于2013年获得3艘18000TEU超大型集装箱船的实船订单,该船入级BV船级社。其主要参数见表1。

表1 主要参数 单位:m
超大型集装箱船有着其他集装箱船甚至大型集装箱船(300m<船长<350m的集装箱船 Very Large Container Ship,(VLCS))所没有的显著特点,这些特点将影响和制约着结构设计。
1 总强度
超大型集装箱船有着显著的大开口特性,并伴随着很大的中拱弯矩。在中横剖面设计过程中,在满足总纵弯曲强度的同时,剖面最小惯性矩的要求也不可忽视。
对于计算船长>350m的船舶, BV和大部分船级社的要求和IACS URS11是一致的,只有GL在波浪系数C的选取上与其他船级社略有差异。
下式为BV和IACS的波浪系数公式,式中L为结构计算船长:
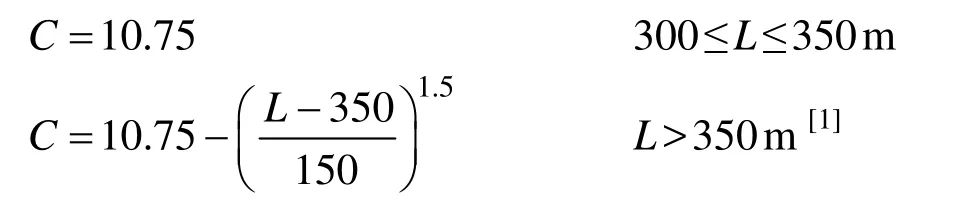
下式为GL的波浪系数公式,式中L为结构计算船长:
C=10.75L>350m[2]
对比两者的公式可以发现,GL对于计算船长大于350m,波浪系数没有折减。
由于集装箱船大开口的特点,在满足总纵强度的前提下,还必须进行弯扭合成应力的校核。各个船级社对于船体梁载荷概率水平也不一样,大部分船级社在合成应力校核时基于10-8,GL基于10-6。各个船级社对于弯扭合成应力计算中的扭矩公式,各个应力分项的系数,合成应力的方法以及应力的衡准都略有差异。
BV的Mars2000软件,提供了基于薄壁梁理论的弯扭合成应力的计算方法,将整个船体从机舱前端壁至防撞舱壁之间的货舱区域模拟成一根变截面梁。考虑到双岛的影响,计算中分成上建前和上建后两个模型,两个模型中对于上建的约束作了不同的处理,最后分别计算各个剖面由于扭矩引起的翘曲应力。
一般来说,最大扭矩发生在船舶斜浪航行的海况下,垂向波浪弯矩是不可能与水平弯矩和扭矩同时达到最大值的。在计算合成应力时,BV规范取40%的最大垂向波浪弯矩值。表2为BV弯扭合成应力的组合系数。

表2 BV规范计算合成应力时弯矩组合系数
对于超大型集装箱船特别是双岛型船型,薄壁梁理论的计算结果,有时会导致船体舭部等合成应力较高的区域板厚增加很多。考虑这些区域的外板为双曲面的板材,太厚的板不利于加工,同时为了优化设计,则可以采用直接在全船有限元模型上直接加载规范载荷进行弯扭合成应力分析。
根据表2,集装箱船全船有限元合成应力分析中加载的载荷,主要考虑垂向弯矩、水平弯矩和扭矩,其中垂向弯矩包括静水弯矩和波浪弯矩,扭矩包含静水扭矩和波浪扭矩。全船有限元模型中,在沿船长方向的一系列纵向节点上仅加载节点力或力偶,通过编程计算各个节点力、力偶的大小来模拟船体梁载荷沿船长的分布。最终依据表2的组合系数将各个分项合成,进行应力校核[3]。
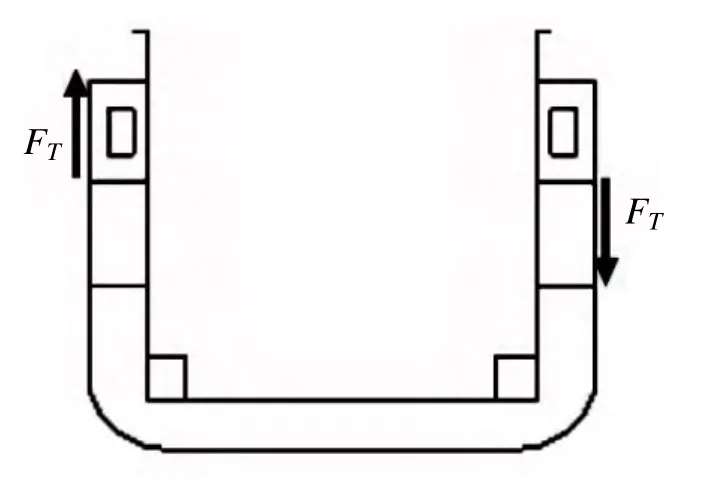
图1 扭矩施加示意
这种方法不仅可以看单个弯矩在船体梁上的纵向应力分项,对于合成的纵向应力也是一目了然。其结果的可靠性和精确度远高于基于薄壁梁理论的计算结果。依据表3,可以把计算工况分为下列4个。

表3 计算工况及弯矩叠加系数
集装箱船或有着大开口船舶必须进行弯扭合成应力的校核。利用薄壁梁理论能快速得到合成应力结果,且工作量小,能作为初始设计依据。对于中小型集装箱船可仅依据薄壁梁理论计算,两者的偏差不大,在可接受的范围内。
全船有限元模型上直接加规范载荷的合成应力分析方法,耗时较多,并且无法在设计初期快速得到结果。但该方法的分析结果更精确,同时考虑到超大型集装箱船必须准备全船有限元模型,此时可以用该方法作为优化设计的手段。
2 舱段有限元
BV在舱段有限元和全船有限元分析中船体梁载荷的超越概率水平为 10-5。对于常规船型的舱段有限元分析,波浪弯矩一般依据规范值进行计算。但考虑到18000TEU集装箱船尺度大,其非线性波浪载荷预报的弯矩值要比规范值大很多。该船在舱段有限元分析中,使用直接预报的非线性波浪弯矩值(概率水平为10-5)作为加载值。下图为该船各个中拱垂向波浪弯矩值的比较。
舱段有限元的模型范围,计算工况及应力、屈曲衡准主要依据 BV要求[4]。模型依据校核区域的不同,模型分为具有3个货舱(第6~第8货舱)的舱段有限元模型和货舱(第6货舱)-深油舱-货舱(第5货舱)的舱段有限元模型。在深油舱有限元模型结构强度校核中,不仅要考虑屈服、屈曲的衡准,也需要核实深油舱舱壁的变形量,以确保变形不会影响到集装箱的正常吊装。两个舱段有限元模型和结果见图3、4。具体的计算工况参看表4、5。

图2 中拱垂向波浪弯矩值比较

图3 货舱舱段有限元模型(左)和深油舱段有限元模型(右)
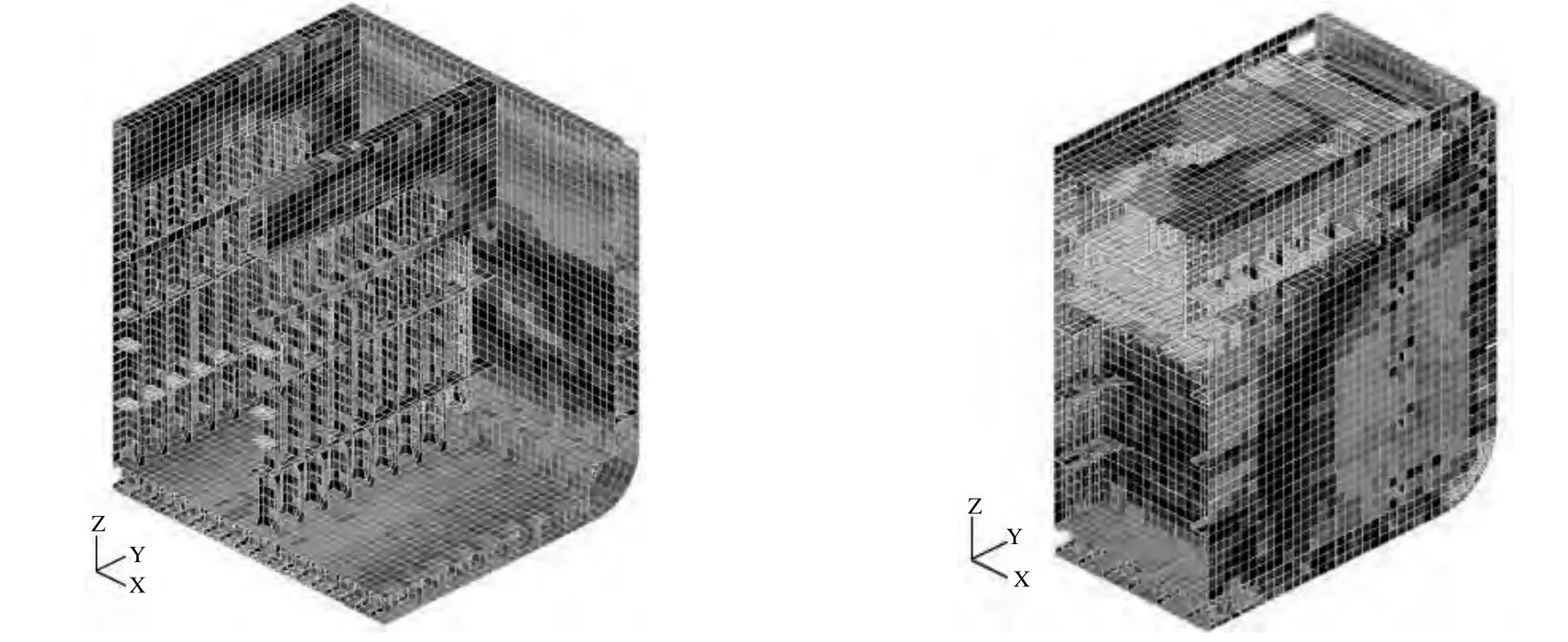
图4 货舱(左)和深油舱(右)von mises应力包络值云图

表4 货舱段有限元分析计算工况

表5 深油舱段有限元分析计算工况
根据BV规范,如果粗网格结果中合成应力超过了衡准的95%,则需要进行细网格的分析[5]。在本船的计算中,根据粗网格的应力结果,对典型强框、水密横舱壁桁材、深油舱水平桁和垂直桁等区域进行细网格有限元分析(见图5)。
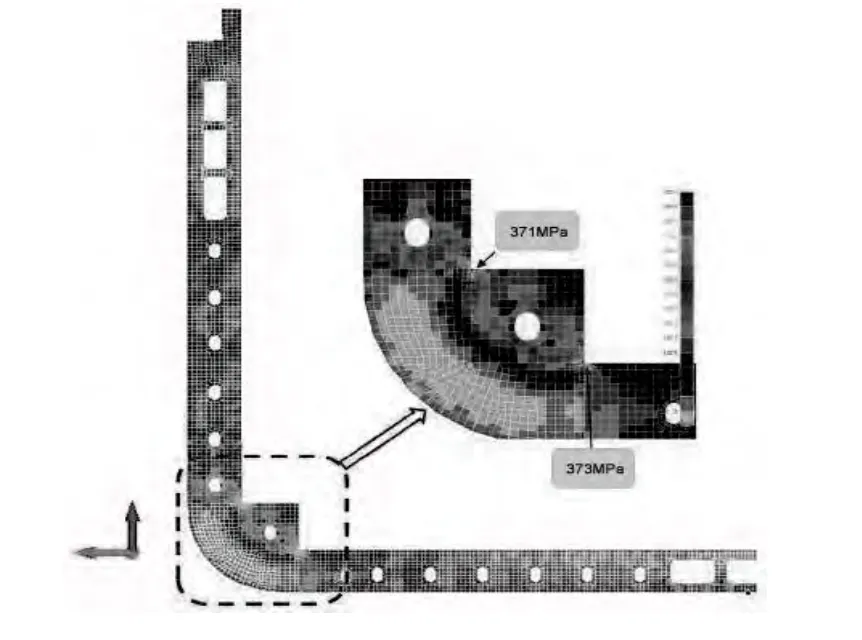
图5 典型强框和局部细网格(小图)的von mises应力包络值云图
3 基于波浪载荷直接预报下的全船有限元
超大型集装箱船由于自身尺度巨大,方形系数较小,并且由于布置要求具有较严重的艏部和艉部外飘。选取超大型集装箱船的设计波浪载荷时,仅仅依赖于规范公式是不够的,须通过直接计算确定波浪弯矩值。
利用谱分析法,进行线性载荷长期值预报,得到垂向波浪弯矩长期值。在计算出线性载荷的长期值后,基于设计海况,进行非线性载荷预报计算,得到每个时间步长下的垂向波浪弯矩长期值,最后进行Weibull分布拟合得到非线性的垂向波浪弯矩的设计值。
得到线型和非线性弯矩的长期值后,可根据规范要求选取计算载况,进行基于设计波法的船体结构强度校核,该船选取了 5个载况[1]。分别为最大垂向波浪弯矩(WBM),水平弯矩(HBM)以及不同位置的波浪扭矩(WT1,WT2,WT3),见表6。

表6 用于全船有限元的5个计算载况及相应的等效设计波
全船有限元的计算工况一般包括压载和满载工况。有限元模型及边界条件可依据船级社规范进行。结果依据船级社要求进行屈服、屈曲校核,部分应力较大的区域还需要进行细网格(50×50)的应力校核(见图6)。

图6 WT1扭转载况下的全船von mises应力分布
4 颤振和弹振
超大型集装箱船由于船长>350m,一阶自然频率通常<0.5Hz,船体的刚度相对较低,并且有较大的艏部外飘;集装箱船的航速较高,与波浪的遭遇频率较易于接近船体自振频率,容易引起颤振和弹振。
颤振(Whipping)是由于冲击载荷,造成船体梁瞬间的响应,使船体总纵弯矩增加。一般情况下,颤振是由艏部拍击、船首底砰击产生的,但有时船尾部砰击也会引起强烈的颤振。通常情况下,颤振响应由于阻尼的影响在波浪的几个周期内会迅速衰减[6],颤振持续的时间较短,一般为0.5~2s[7],但对船体梁的极限强度影响较大。
弹振(Springing)是由波浪引起的船体梁振动响应。当船体梁固有频率与波浪遭遇频率接近时更易产生。相对于颤振而言,弹振响应所持续的时间会更长,对船体结构的疲劳强度影响较大。
颤振分析是基于非线性水弹性方法,在时域中进行,航速取 5kn,基于北大西洋波浪散布图谱,10-8载荷概率水平[5]。通过计算,各个剖面的垂向波浪弯矩的设计值见图7。船体剖面的极限强度由Mars2000软件得到,不同于常规规范极限强度校核,用于颤振极限强度校核时,船体构件只扣除1/2腐蚀余量。根据规范要求,还需要考虑1.1的安全系数。船体梁极限强度校核见图8。
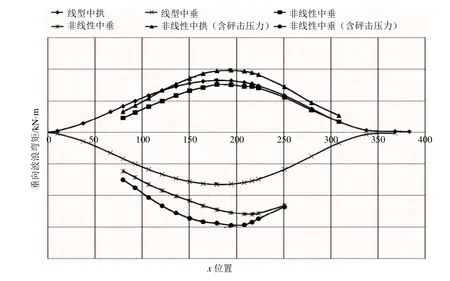
图7 线性、非线性垂向波浪弯矩长期预报值
超大型集装箱船由于船体固有频率较低,弹振对于构件疲劳寿命的影响显而易见。弹振的响应在垂向波浪弯矩的 2阶振动时达到最大[8]。有研究表明,弹振能减少构件、节点的疲劳寿命平均达30%~40%;对个别关键节点,弹振对疲劳寿命的影响更大,有的甚至达到70%。由于颤振发生的瞬时性,颤振对于疲劳的影响,业内尚存在不同意见,该船节点的疲劳寿命分析仅考虑弹振的影响。
弹振发生的海况没有颤振恶劣,所以速度的影响更明显。弹振分析是基于线性水弹性方法,在频域中进行,航速取 0.6倍的最大航速,基于全球波浪散布图谱[7]。

图8 船体梁的极限强度校核(极限弯矩已包含安全系数)
弹振计算包含由于船体结构振动而引起的变形。在进行水弹性弹振计算时,先要进行模态分析,在得到船体梁的振型之后,将振型投射到水动力网格上进行水弹性波浪载荷计算,之后将波浪载荷与结构的动态响应进行组合,得到最终的结果。分别计算了船体梁前五阶干模态和湿模态,计算结果见表7。

表7 各阶模态干模态和湿模态的固有频率/(°)·s-1
该船有BV船级社的WhiSp2船级符号,根据规范要求,需要满足疲劳寿命28a(考虑线性弹振的影响)。选取约122个典型节点,节点覆盖整船所有疲劳关键区域。分别计算了各个节点的准静态(不考虑弹振的影响)和水弹性(考虑弹振的影响)的疲劳寿命。
部分节点的热点应力传递函数见图9。图中曲线分别为不计弹振效应(刚体准静态)的应力传递函数、弹振效应引起的应力传递函数以及合成的应力传递函数。从结果可以看出,在高频区域,弹振效应引起的应力响应与刚体应力响应相比,增加非常显著。图 10中还显示了在疲劳谱分析计算时,各个浪向和海况对节点总的疲劳累积损伤的贡献。基于这结果,对于疲劳寿命没有达到要求的节点需要进行节点设计改进的时候,可以通过利用某一浪向下的设计波进行检验不同的设计方案,以减小计算量并快速得到可满足疲劳寿命要求的节点形式。

图9 FR84-Fr94机舱甲板开口处 热点应力传递函数
在结构设计过程中,对于疲劳寿命无法满足要求的节点,须作改进优化,再重新计算,直到疲劳寿命满足要求为止。但是,基于弹振的疲劳谱分析方法计算量巨大,成本极高而且非常耗时,无法进行大量方案的对比计算。所以需要找到合适的简化方法来考察节点的疲劳强度特性,如节点应力水平和应力集中系数等。机舱区域“T”型平台的前后节点都处于结构形式的突变处,应力集中现象较为严重,普通的节点形式很难满足疲劳寿命要求。
由于这两个节点分别处于机舱与前后货舱的交界处,位于纵舱壁和横舱壁的交点,扭矩对此类节点的疲劳强度起决定性的作用,所以可以利用以扭矩为主的60°和120°浪向下的设计波,来计算两个节点处的应力水平与应力分布。在计算时采用了子模型的方法,无需对整船模型重新计算。先定义子模型边界上与全船模型上的主从节点,将全船模型的变形传递到子模型上作为边界条件进行计算。结果见下表。
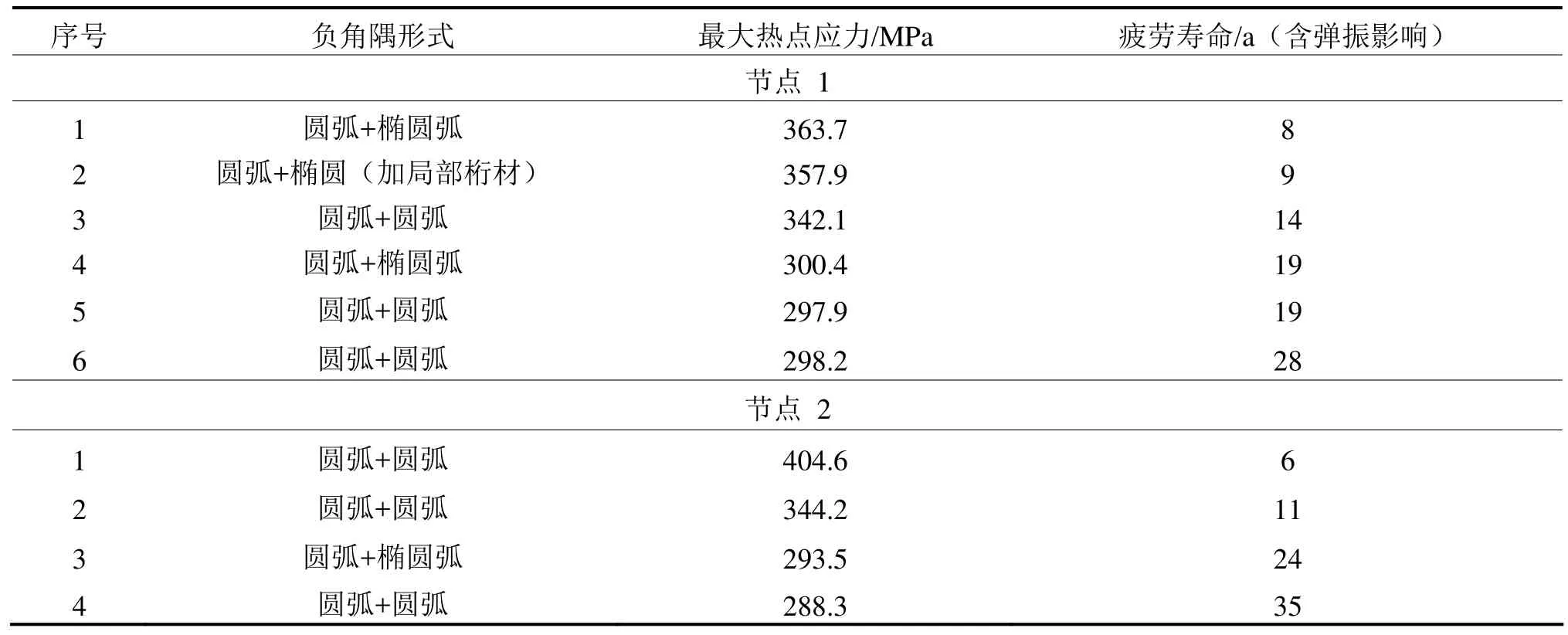
表8 两个节点的不同形式下的最大应力和疲劳寿命
由表8可知,随着热点应力的降低,疲劳寿命一般会提高。但这并不绝对,如节点1中的方案4~方案6。热点应力只能代表特定海况单一浪向下的应力值,由图10可知,对疲劳起贡献作用的是一定范围内的海况和浪向的组合。
最终所有节点的疲劳寿命均达到28a(含弹振的影响),若仅考虑刚体结构响应(不含弹振的影响),上述节点1、节点2的疲劳寿命均远远大于40a,由此可见,弹振对于关键区域节点的疲劳寿命影响非常大。
颤振和弹振的分析计算过程中,依据它们各自不同的现象起源,假定它们不会同时出现[7],分别进行计算而不考虑它们之间的影响。通常,颤振影响船体的极限承载能力,弹振对结构的疲劳寿命影响较大。
5 结 语
18000TEU是国内第一艘自主研发设计的超大型集装箱船,除常规的结构分析计算外,还进行了基于水弹性的颤振和弹振分析,各项技术指标达到设计要求。
超大型集装箱船由于相对较高的航速,大开口,且L>350m,并伴有明显的艏部外飘,因此一阶固有频率很低,与遭遇的波浪频率接近,容易产生颤振和弹振现象,易对船体结构造成破坏。相对于其他集装箱船乃至大型集装箱船,超大型集装箱船的结构设计中应注意以下几点:
1) 在总强度计算中,有时需要通过直接计算来优化构件尺寸;
2) 舱段和全船有限元有时仅仅依据规范的弯矩值不能满足设计要求,需要采用线性或非线性载荷分析的弯矩值;
3) 颤振和弹振对于超大型集装箱船的影响非常明显,对船体结构的极限强度和疲劳强度的影响较大。
[1] BV. Rules for the Classification of Steel ships[S]. 2013.
[2] GL. Rules for Classification and Construction Ship Technology[S]. 2013.
[3] DNV. Strength Analysis of Hull Structures in Container Ships[S]. 2011.
[4] BV. Structural Analysis of Container Ships[S]. 2008.
[5] BV. Ultra Large Container Ships[S]. 2010.
[6] Nigel White, Zhenhong wang, Yongwon Lee. Guidance Notes on Whipping and Springing Assessment[R], IMDC. 2012.
[7] ABS. Whipping Assessment for Container Carriers[S]. 2010.
[8] ABS. Springing Assessment for Container Carriers[S]. 2010.
