不同土体对迫击炮射击稳定性影响的动力学分析

徐晓乐，刘树华

（中北大学 机电工程学院，山西 太原 030051）

0 引言

鉴于现代作战模式与战场环境中迫击炮已成为陆战场不可或缺的火力支援兵器，如何适应现代战场环境成为迫击炮研究的重点，其中轻量化是其主要方向之一。本文应用CAE技术对迫击炮后坐复进运动进行分析，进而对迫击炮射击稳定性进行分析和预测，为迫击炮轻量化设计提供理论基础。

1 迫击炮后坐系统动力学分析

1.1 后坐系统运动微分方程

通过分析迫击炮后坐运动过程，得到其动力学微分方程如下：

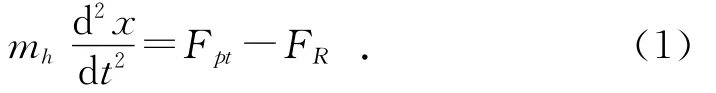
其中：mh为全炮质量；x为后坐位移；Fpt为炮膛合力；FR为后坐阻力，FR＝R（t）＋Fc＋Fz＋Ff，R（t）为土壤抗力，Fc为阻尼力，Fz为缓冲簧的缓冲力，Ff为系统的摩擦力。

迫击炮复进运动微分方程为：

1.2 迫击炮缓冲机中缓冲簧阻力

图1为迫击炮缓冲机结构示意图。

计算缓冲机弹簧力时，对后坐阶段和复进阶段分别计算。后坐阶段缓冲机弹簧力为：

复进阶段缓冲机弹簧力为：

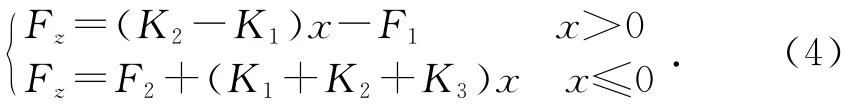
其中：K1，K2，K3分别为缓冲结构中弹簧1，2，3的刚度；F1，F2分别为弹簧1，2的初始力；x为后坐位移，当x＞0时，座钣与土壤接触，当x≤0时，座钣与土壤不接触。

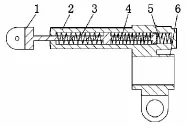
图1 迫击炮缓冲机结构示意图

2 动力学仿真及结果分析

2.1 动力学模型

图2为基于Simulink的后坐系统仿真模型。

图2 后坐系统仿真模型

2.2 动力学仿真与结果分析

本文的研究对象是迫击炮在射角45°主射击平面内的射击稳定性，利用ANSYS软件对模型进行动力学分析，计算得到全装药时在硬土、中硬土、软土3种土壤情况下后坐部分的位移、速度以及后坐阻力的变化曲线。

（1）图3～图5分别为硬土情况下后坐部分的速度、位移及后坐阻力的变化曲线。

（2）图6～图8分别为中硬土情况下后坐部分的速度、位移及后坐阻力的变化曲线。

（3）图9～图11分别为软土情况下后坐部分的速度、位移及后坐阻力的变化曲线。

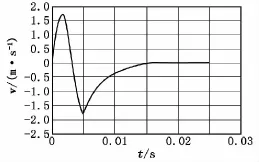
图3 硬土时后坐部分速度v－t曲线

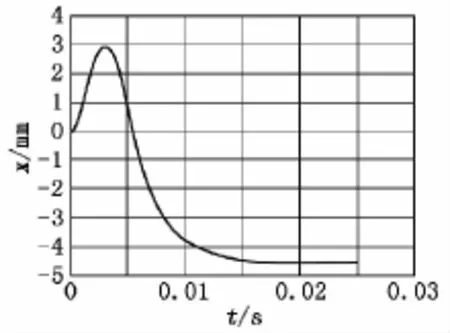
图4 硬土时后坐部分位移x－t曲线

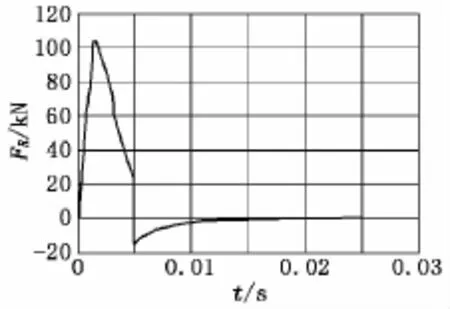
图5 硬土时后坐阻力FR－t曲线

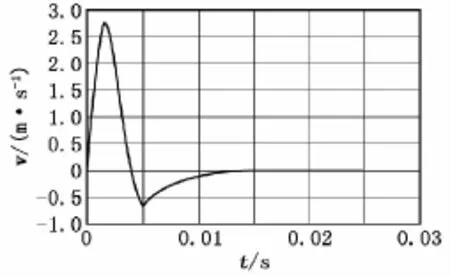
图6 中硬土后坐部分速度v－t曲线

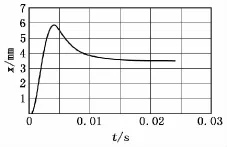
图7 中硬土后坐部分位移x－t曲线

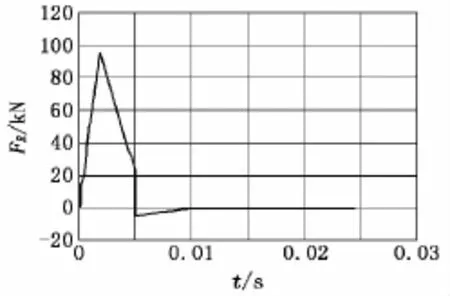
图8 中硬土后坐阻力FR－t曲线

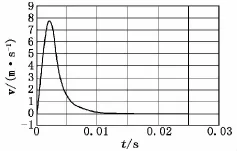
图9 软土后坐部分速度v－t曲线

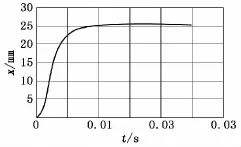
图10 软土后坐部分位移x－t曲线

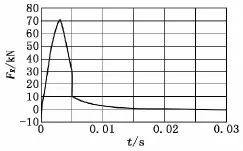
图11 软土后坐阻力FR－t曲线

表1为后坐部分在3种土壤中的运动极限值。由图4、图7和图10可知：硬土中后坐部分跳离地面大约为4.80mm；中硬土中后坐部分复进回弹大约为3.60mm；在软土中后坐部分没有复进回弹。

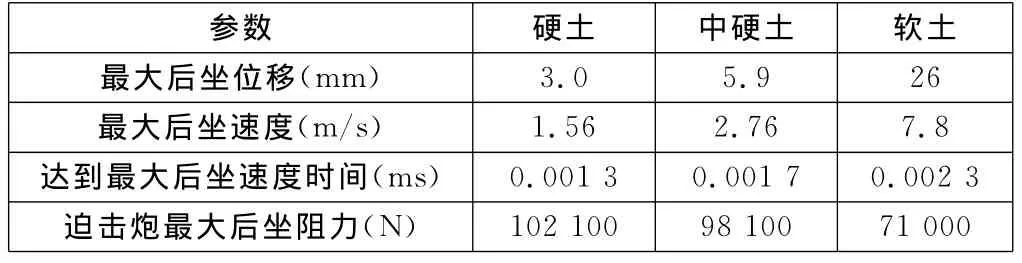
表1 后坐部分在3种土壤中的运动极限值

3 结束语

本文应用ANSYS软件对迫击炮的后坐系统在3种类型土壤45°角射击进行动力学仿真。数值计算结果很好地表明了迫击炮在不同类型土壤射击情况下的稳定性，为下一步迫击炮轻量化及其他优化设计提供了参考。

［1］唐治.迫击炮设计［M］.北京：兵器工业出版社，1994.

［2］鲍廷玉，邱文坚.内弹道学［M］.北京：北京理工大学出版社，1995.

［3］薛定宇，陈阳泉.基于MATLAB/Simulink的系统仿真技术与应用［M］.北京：清华大学出版社，2002.

［4］陈运生，杨国来.火炮发射动力学仿真［M］.北京：国防工业出版社，2003.

［5］宋德军.近战利器——现代迫击炮［J］.国防科技，2006（2）：10-12.