环R上的一类常循环码及自对偶码

徐露露， 刘 丽

（合肥工业大学 数学学院，安徽 合肥 230009）

自从文献［1］证明了某些二元非线性码可以看作Z4线性码在Gray映射下的二元象之后，有限环上纠错码理论就成为研究的一个新热点，从此Gray映射是连接环上码与域上码的关键点，所以被众多学者加以重新定义和研究［2－8］。文献［3－4］中引入了一个 Nechaev－Gray映射，研究了Z4上负循环码的Gray映射，随后，多项式剩余类环介于有限域和环之间的良好结构性质，在纠错码理论研究上备受关注。文献［9］首次研究了F2＋uF2上常循环码的Gray象性质，随后，文献［10］又研究了F2m＋uF2m＋…＋ua－1F2m上形如（α0＋uα1＋…＋ua－1αa－1）循环码结构。本文在环R＝F2＋uF2＋u2F2＋…＋u7F2上，重新定义一种新的 Gray映射，研究η＝（1＋u＋u2＋u3＋u4＋u5＋u6＋u7）循环码的 Gray象，在该映射之下，环R上线性循环码能等距映射成域F2的线性循环码，并给出n为奇数时该码的Gray象的生成多项式。

1 环R上的循环码与η循环码

定义1 设C为R上长为n的线性码，如果∀c＝ （c0，c1，…，cn－1）∈C均 有 （λcn－1，c0，…，cn－2）∈C，此时称（λcn－1，c0，…，cn－2）为（c0，c1，…，cn－1）的一个λ循环移位，则称C为R上的λ循环码。若λ＝1，则称C为R上的循环码，若λ＝1＋u＋u2＋u3＋u4＋u5＋u6＋u7（记为η），则称C为R上的η循环码。

定义2 如果设C、C1是Rn的2个子空间，对于任意的a＝（a0，a1，…，an－1）∈C，β＝（b0，b1，…，bn－1）∈C1，恒有a0b0＋…＋an－1bn－1＝0，则称C、C1为正交的。如果C＋C1＝Rn，则称C1为C的正交补，将它记做C⊥，并称之为C的对偶码，若C⊥＝C，则称C为自对偶码。

对码字c＝（c0，c1，…，cn－1）∈C的码字多项式，即对应R［x］／（xn＋η）中的多项式c（x）＝c0＋c1x＋…＋cn－1xn－1，类似于文献［4］，有如下结论。

定理1Rn上子模是R上η循环码⇔c（x）是环Bn＝R［x］／（xn＋η）的理想。

假设n为奇数，k为一个正整数，若n≡3（mod 4），则设β＝η；若n≡1（mod 4），则设β＝1＋u。注意到βn＝1＋u，且（1＋u）η＝1。

设μ是如下映射：R［x］／（xn＋1）→R［x］／（xn＋η），μ（c（x））＝c（βx）。则有如下定理2。

定理2 设β如上所述，则μ是R［x］／（xn＋1）到R［x］／（xn＋η）的环同构映射。

故有推论1。

推论1 设I是R［x］／（xn＋1）的子集，J是R［x］／（xn＋η）的子集，n为奇数，并满足J＝μ（I），则I是R［x］／（xn＋1）的理想，当且仅当J是R［x］／（xn＋η）的理想。

文献［11］给出了环Fp＋uFp＋…＋uk－1Fp上循环码的结构，类似地有定理3。

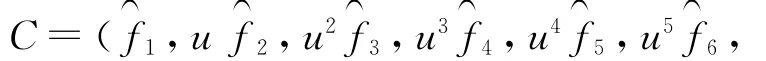
利用上面的同构映射μ，得定理4。

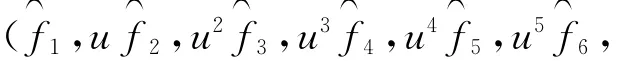
2 R上η循环码的Gray象

为不致引起混淆，将R、Rn、R［x］上加法记为“＋”，将F2、、F2［x］上加法记为“⊕”。若将R上任一元素a记为a＝r0（a）＋ur1（a）＋u2r2（a）＋…＋u7r7（a），其中ri（a）∈F2，参考文献［7－8］，定义Gray映射φ：R→，则

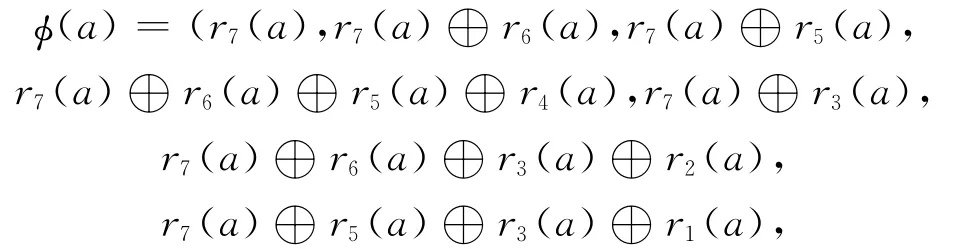
显然该映射是线性的，可自然延伸至Rn上码字C的Gray映射以及R［x］上多项式c（x）的Gray映射φ：R→，则

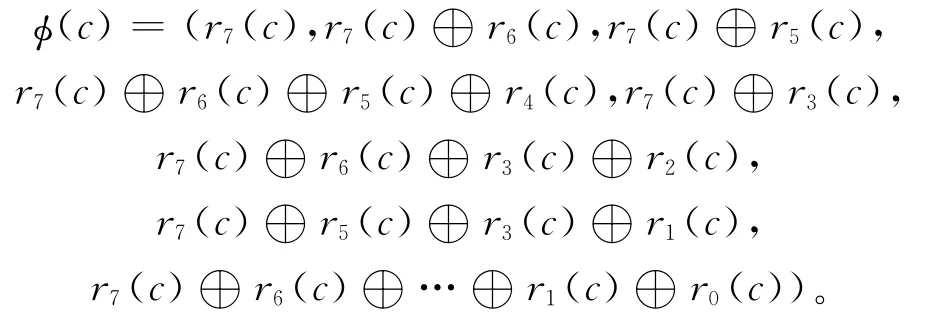
其中c＝（c0，c1，…，cn－1）∈Rn。记ri（c）＝（ri（c0），ri（c1），…，ri（cn－1）），i＝0，1，2，…，7，φ显然是双射，对∀c（x）＝c0＋c1x＋…＋cn－1xn－1∈R［x］，设

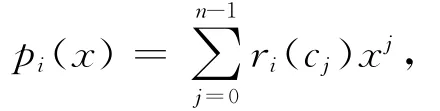
其中，i＝0，1，…，7。则φ：R［x］→F2［x］，即

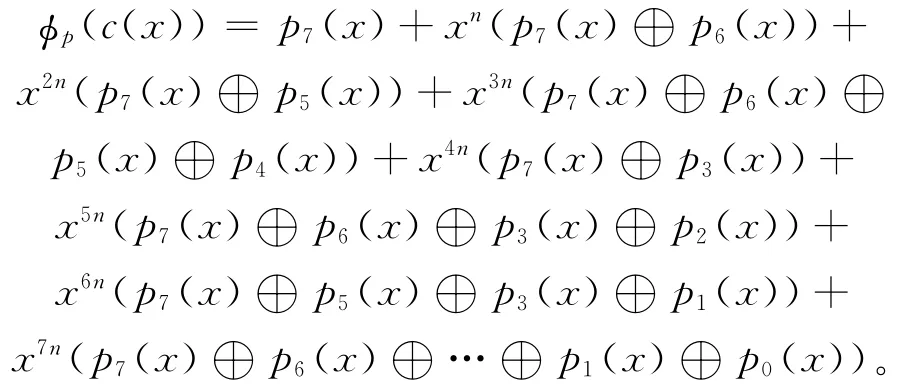
定义环R中元素的Lee重量分别如下：u8为8；1＋u，1＋u2＋u3＋u6，1＋u4＋u5＋u6，1＋u2＋u3＋u4＋u5＋u6，1＋u＋u2＋u3＋u4＋u5＋u6为7；u＋u7，u2＋u7，u4＋u7，1＋u4＋u5＋u7为6；1＋u5，1＋u6，1＋u＋u6，1＋u＋u7，1＋u2＋u5，1＋u2＋u7，1＋u3＋u4，1＋u3＋u5，1＋u3＋u6，1＋u4＋u7，1＋u5＋u6，1＋u＋u2＋u4，1＋u＋u2＋u5，1＋u＋u2＋u6，1＋u＋u2＋u7，1＋u2＋u3＋u4，1＋u2＋u3＋u5，1＋u2＋u3＋u7，1＋u3＋u4＋u5，1＋u2＋u3＋u4＋u6，1＋u＋u2＋u3＋u5，1＋u＋u2＋u3＋u6，1＋u＋u2＋u3＋u7，1＋u3＋u4＋u5＋u6，1＋u2＋u3＋u4＋u5＋u7，1＋u＋u2＋u3＋u4＋u5，1＋u＋u2＋u3＋u4＋u6，1＋u＋u2＋u3＋u4＋u7为5；u6，u5，u3，u5＋u6，u5＋u7，u6＋u7，1＋u＋u2，1＋u3＋u4＋u6为4；u4，u2，u，u＋u2，u＋u3，u＋u4，u＋u5，u2＋u3，u2＋u4，u2＋u5，u2＋u6，u4＋u5，u4＋u6为2；1，1＋u4＋u5＋u6＋u7，1＋u＋u2＋u3＋u4＋u5＋u6＋u7为1；0为0；其余为3。

Rn中码字的Lee重量为其码元的Lee重量之和，2个码字c、c′的Lee距离为c－c′的Lee重量。由Gray映射定义可得定理5～定理8。

定理5 Gray映射φ是（Rn，Lee距离）到（，Hamming距离）的保距映射。

定理6 若ν是Rn上一个η循环移位，σ是上的一个循环移位，φ是Rn到的Gray映射，则φν＝σφ。

证明 设c＝（c0，c1，…，cn－1）∈Rn，其中ci＝r0（ci）＋ur1（ci）＋u2r2（ci）＋ … ＋u7r7（ci），rj（ci）∈F2，i＝0，…，n－1，j＝0，1，…，7，则有：

定理7 设C为R上长为n的线性η循环码，则其Gray象φ（C）是F2上长为8n的线性循环码。

沿用文献［6］中定义，对于c＝（c0，c1，…，cn－1）∈Rn，记ri（c）＝ ［ri（c0），ri（c1），…，ri（cn－1）］，其中，i＝0，1，2，…，7，则称＝r0（c）为c的二元约化。类似地，若R［x］，则称∈F2［x］为a（x）的二元约化，显然有

定理8 若C是环R上长度为n（n为奇数）的η循环码，且

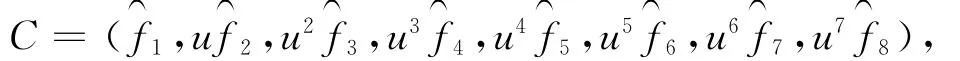
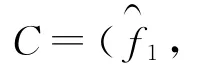
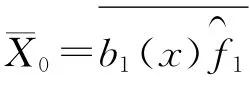
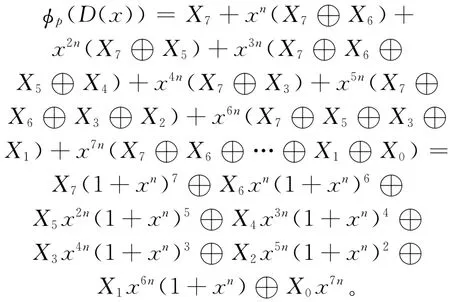
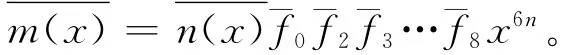
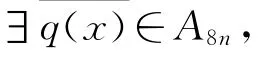
3 环R上的自对偶码

引理1 设C是R上长为n的线性码，C的特征是p，｜C｜＝pk，｜R｜＝pm，则｜C⊥｜＝pl，其中k＋l＝mn。

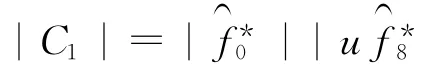
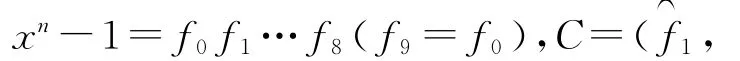
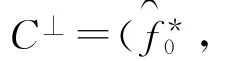
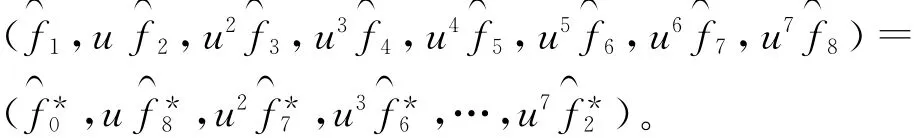
设Gi＝，i＋j≡1（mod 9）（i，j＝0，1，…，8），其中，G0，G1，…，G8是两两互素的不可约多项式，所以－G0G1…G8＝xn－1＝f0f1…f8，由定理3得Gi＝Fi，i＋j≡1（mod 9）（i，j＝0，1，…，8）。

4 结束语

本文定义了环R＝F2＋uF2＋u2F2＋…＋u7F2到的一个新的Gray映射，将环R上长为n的一类常循环码等距映射成F2上长为8n的线性循环码，研究了该环上（1＋u＋u2＋u3＋u4＋u5＋u6＋u7）循环码的Gray象，并给出了n为奇数时该码的Gray象的生成多项式。此外，还得到了在这个环上的自对偶码存在的一个充要条件，对于构造一些高效且纠错性能好的码和译码，具有一定的理论意义和应用价值。

［1］ Hammons A R，Kumar P V，Calderbank A R，et al．TheZ4－linearity of Kerdock，Preparata，Goethals，and related codes［J］．IEEE Trans Inform Theory，1994，40（2）：301－319．

［2］ Bonnecaze A，Udaya P．Cyclic codes and self－dual codes overF2＋uF2［J］．IEEE Trans Inform Theory，1999，45：1250－1255．

［3］ Wolfmann J．Negacyclic and cyclic codes overZ4［J］．IEEE Trans Inform Theory，2001，47（5）：1773－1779．

［4］ Wolfmann J．Binary images of cyclic codes overZ4［J］．IEEE Trans Inform Theory，1999，45（7）：2527－2532．

［5］ Bonnecaze A，Udaya P．Decoding of cyclic codes overF2＋uF2［J］．IEEE Trans Inform Theory，1999，45（6）：2148－2157．

［6］ Zhu S X，Wang L Q．A class of constacyclic codes overFp＋uFpand its Gray image［J］．Discrete Mathematics，2011，311（23／24）：2677－2682．

［7］ 朱士信，吴 波．环Fp＋uFp＋…＋ukFp上的线性码和常循环码的Gray像［J］．合肥工业大学学报：自然科学版，2006，29（8）：1049－1052．

［8］ 李 岩，朱士信．环Fpm＋uFpm＋…＋u（k－1）Fpm上的一类常循环码［J］．合肥工业大学学报：自然科学版，2012，35（3）：408－411．

［9］ Qian J F，Zhang L N，Zhu S X．（1＋u）constacyclic and cyclic codes overF2＋uF2［J］．Applied Mathematics Letters，2006，19（8）：820－823．

［10］ Dinh H Q，Nguyen H D T．On some classes of constacyclic codes over polynomial residue rings［J］．Advances in Mathematics of Communications，2012，6（2）：175－191．

［11］ Qian J F，Zhang L N，Zhu S X．Cyclic codes overFp＋uFp＋…＋uk－1Fp［J］．IEICE Transactions on Fundamentals of Electronics，Communications and Computer Sciences，2005，E88－A（3）：795－797．