一个三维四翼混沌系统的分岔分析及其电路实现

鲍慧玲， 薛 华

（1.上海科学技术职业学院 通信与电子信息系，上海 201800；2.滨州学院 物理与电子科学系，山东 滨州 256603）

20世纪60年代，Lorenz系统被提出，此后混沌理论及混沌系统的复杂动力学特性，引起了人们的广泛关注和深入研究［1－3］。混沌的内随机性、遍历性和普适性使其在保密通信和数字图像信息加密等信息安全领域具有更广阔的应用前景［4－7］。近年来，各种四翼混沌系统不断出现，文献［8］提出了一个伪四翼混沌系统；文献［9］提出了一个新的四翼混沌系统；文献［10］提出了一个可以产生四翼混沌吸引子的超混沌系统。

本文在文献［8］提出的伪四翼混沌系统的模型下，引入状态变量x的正反馈，生成了一个新的三维四翼混沌系统。

该系统关于y轴对称，有5个系统参数和3个二次交叉乘积项，包含5个平衡点，在其中2个对称平衡点处发生Hopf分岔行为，系统由不动点演变为周期轨。对系统整体动力学特性变化进行了研究，分析了Lyapunov指数和分岔图，揭示了参数变化时系统轨迹由不动点、周期轨到混沌吸引子的变化过程。同时，通过硬件电路对系统进行了验证。

1 三维四翼混沌系统

文献［8］提出的伪四翼混沌系统为：

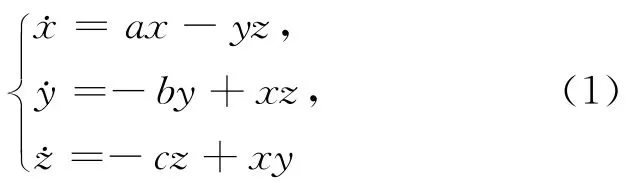
通过在系统的第3式中引入变量x的正反馈，可以生成一个新的三维四翼混沌系统，该系统存在着复杂的动力学行为，即

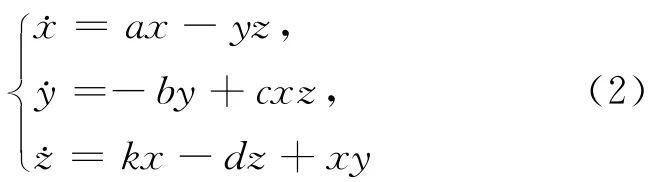
其中，系统参数a、b、c、d、k均大于0。

三维四翼混沌系统的5个平衡点S1、S2、S3、S4、S5分别为：

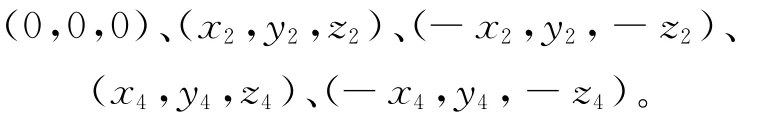
其中

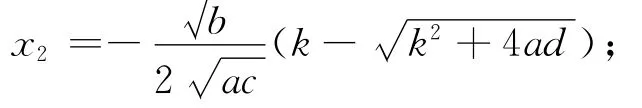
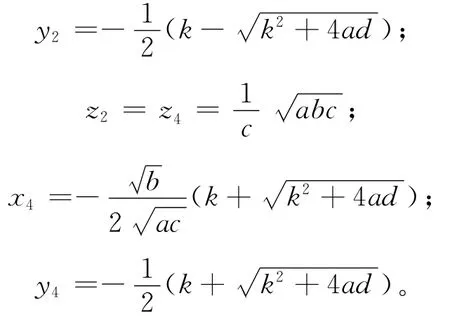
当a＝3、b＝8、c＝4、k＝1、d＝2时，系统平衡点为：

此时系统呈现混沌状态。通过大量的数值仿真，发现系统在较宽的参数范围内能生成四翼混沌吸引子。图1所示为三维四翼混沌系统的相平面图。

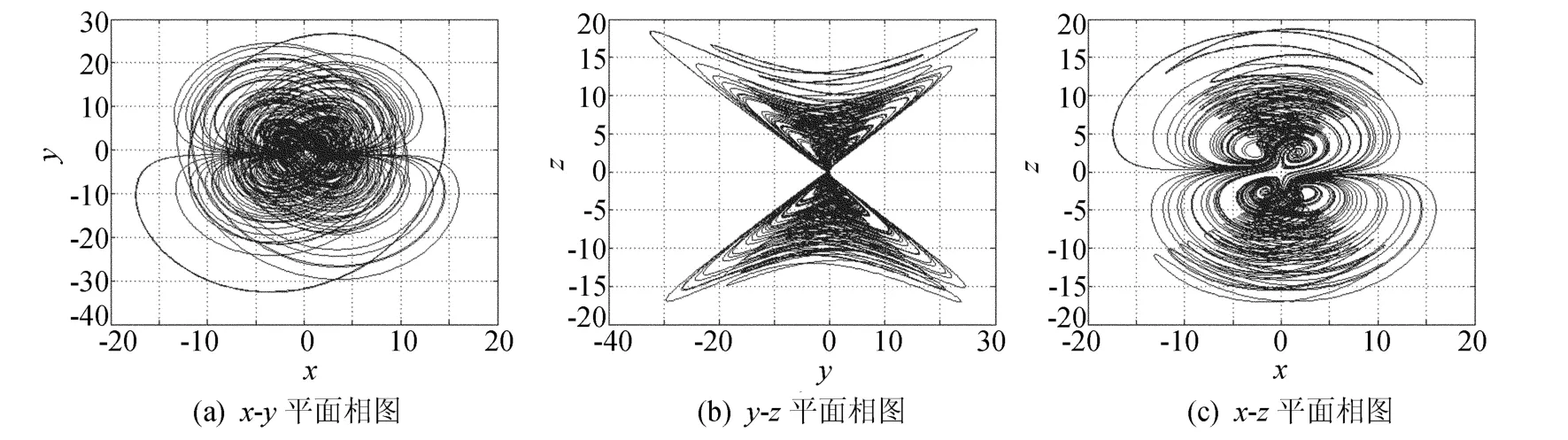
图1 三维四翼混沌系统的相平面图

1.1 耗散性

当系统参数b＞0、d＞0、a＜0时，可得：

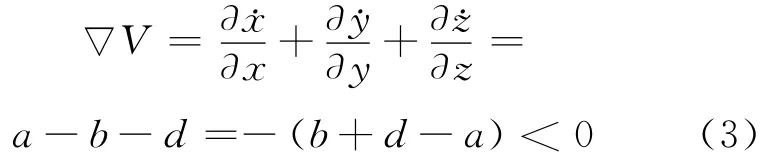
根据各参数取值，▽V＝－（b＋d－a）＝－7＜0，系统为耗散性系统，并按照指数速率收敛，即dV／dt＝e－（b＋d－a）t＝e－7t，系统轨迹按照指数速率收缩到0，其动力学行为被局限在一个吸引子上。

1.2 对称性

通过代数变换和平衡点分析，可知系统关于y轴对称，其中平衡点S2与S3，S4与S5都关于y轴对称，这2组平衡点对具有相同的局部稳定性和中心流行。但是系统关于x轴、z轴和原点都是不对称的，这些不对称性意味着系统有着更丰富的动力学行为。

1.3 Hopf分岔分析

（2）式在各个平衡点的Jacobian矩阵通式可以表示为：

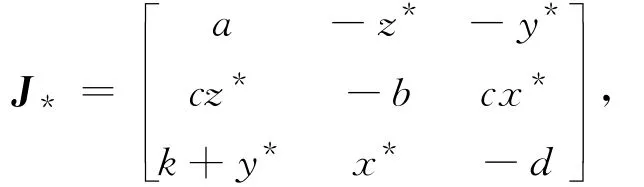
其中，x＊、y＊、z＊分别代表平衡点S1～S5的坐标值。

平衡点S1（0，0，0）处的Jacobian矩阵为：

其特征值方程为｜J1｜－λI＝0，得到平衡点S1处的特性方程为：

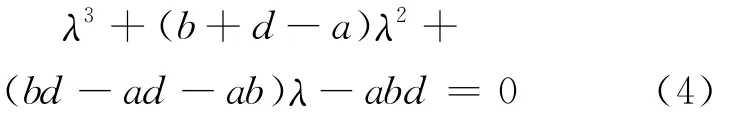
简化方程得：

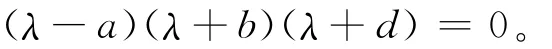
特征方程有3个特征根，λ1＝a，λ2＝－b，λ3＝－d，系统中的参数a、b、c、d、k均大于0，该系统的平衡点S1为一个鞍点，故在平衡点S1处不可能发生 Hopf分岔行为。平衡点S2＝（x2，y2，z2）处的Jacobian矩阵为：

其特征值方程为｜J2｜－λI＝0，得到平衡点S2处的特性方程为：

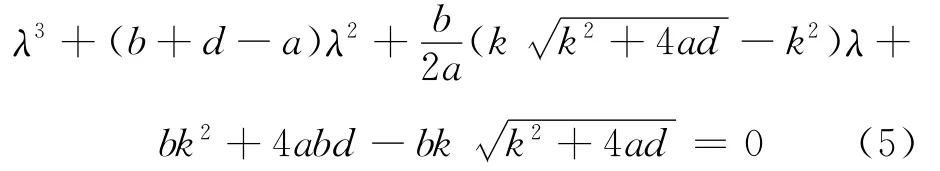
根据Routh－Hurwitz稳定判据，当下列不等式成立时，（5）式的特征根都具有负实部，平衡点S2为稳定的平衡点。不等式如下：随着参数a的变化，若不满足上述不等式时，

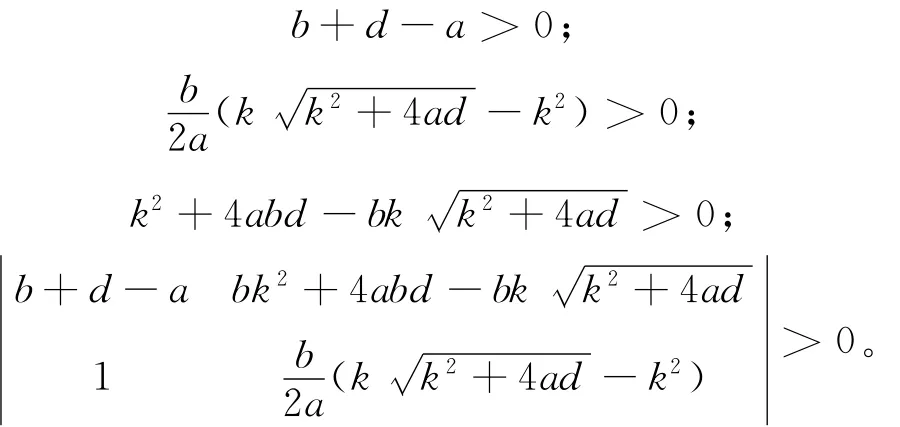
平衡点S2将失去稳定性。当下式成立时，特征方程具有一对纯虚根，即

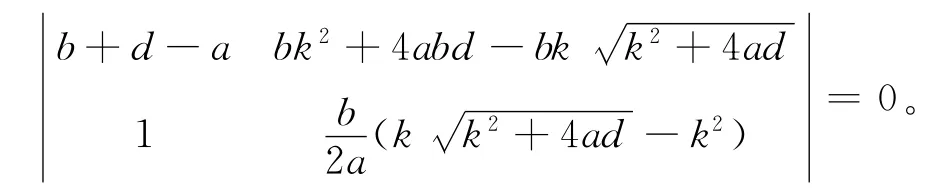
固定系统参数b＝8，c＝4，k＝1，d＝2，当a＝1.292 7时，（5）式的特征根分别为λ1，2＝±2.706 7i，λ3＝－8.707 3，（5）式很明显具有1对纯虚根，根据Routh－Hurwitz稳定判据，平衡点S2在a＝1.292 7处发生了Hopf分岔。

通过数值分析，平衡点S2处的Hopf分岔是一个前向分岔过程，当a＜1.292 7时，平衡点S2是一个稳定的平衡点。当a≥1.292 7时，平衡点S2不稳定，系统轨迹离开平衡点S2趋于一个稳定的周期轨。由于S2，3是一组对称平衡点，在局部范围内有相同的稳定性质，所以，在S3处发生同样的Hopf分岔，发生Hopf分岔的参数条件和S2处的参数条件一致。平衡点S4＝（x4，y4，z4）处的Jacobian矩阵为：

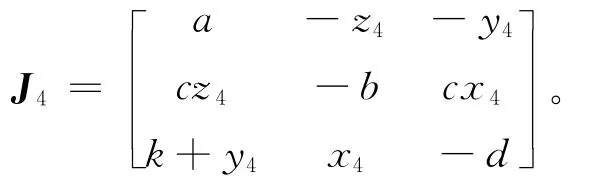
其特征值方程为｜J4｜－λI＝0，得到平衡点S4处的特性方程为：

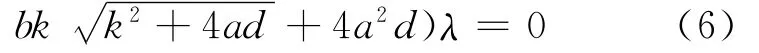
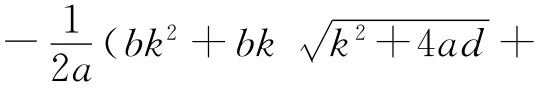
2 数值分岔分析

对于一个连续的非线性动力系统，系统参数改变能引起整个系统动力学行为的复杂变化，当参数取值变化时，系统轨迹会经历平衡点、周期、拟周期及混沌等。Lyapunov指数图和分岔图能呈现出动力系统随参数变化的过程，如图2所示。

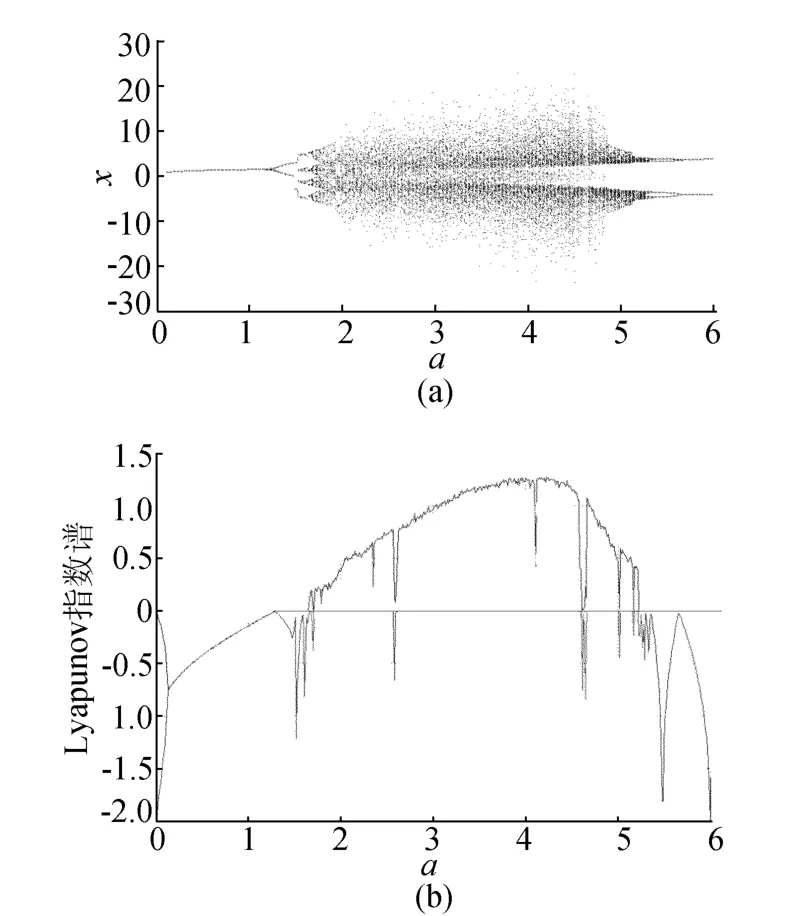
图2 参数a的数值分岔分析

从图2可以看出，随着参数a的变化，系统轨迹从不动点到周期吸引子、混沌吸引子。从Lyapunov指数谱可以看出，当a属于［0，1.292 7），Lyapunov指数都小于0，系统轨迹收敛于一个不动点；当a属于［1.292 7，1.75），Lyapunov指数1个为0，其余为负，系统轨迹为周期状态。其中，a属于［1.292 7，1.43］时，系统轨迹为一个单周期轨道；a属于［1.43，1.56］时，系统轨迹为一个双周期轨道；a属于［1.56，1.75］时，系统轨迹为一个三周期轨道。系统从平衡点演变为周期轨道，也证实了a＝1.292 7时，系统在平衡点处发生了Hopf分叉行为。当a属于［1.75，5.3］时，Lyapunov指数1个为正，1个为0，其余为负，系统轨迹为混沌状态。

如图3所示，当参数a取不同数值时，系统呈现出单周期轨道、双周期轨道、三周期轨道以及混沌吸引子等运动形式，表明系统具有丰富的动力 学行为。

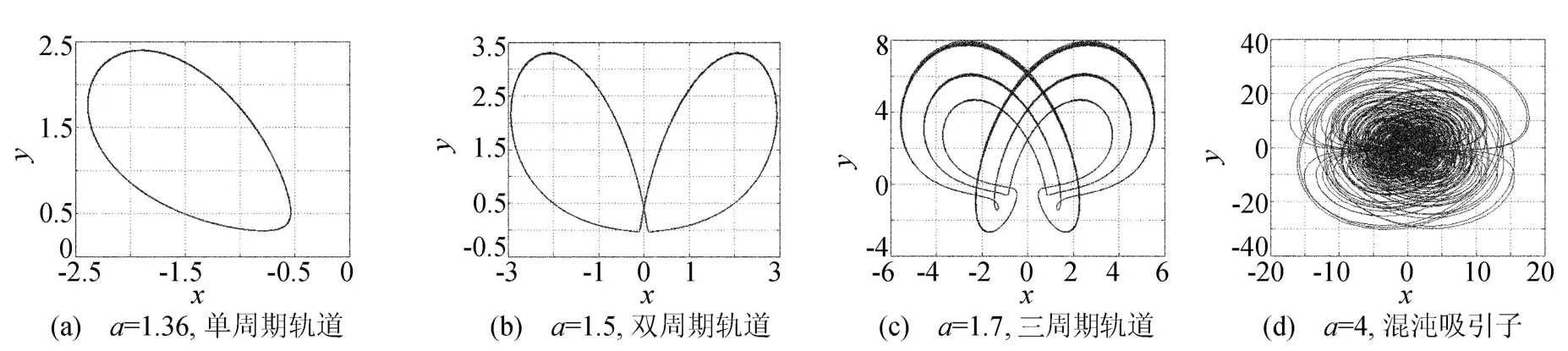
图3 b＝8，c＝4，d＝2，k＝1时系统x－y平面相图

3 系统电路的实现

为了进一步验证三维四翼混沌系统的存在，利用模拟电路器件构建了这一混沌系统的硬件电路，该电路采用运算放大器（TL082）和基本的电阻、电容（1μF）等元器件，实现了求和、积分及反相等运算，模拟乘法器（AD633）用来实现非线性乘积运算，电路结构图如图4所示。

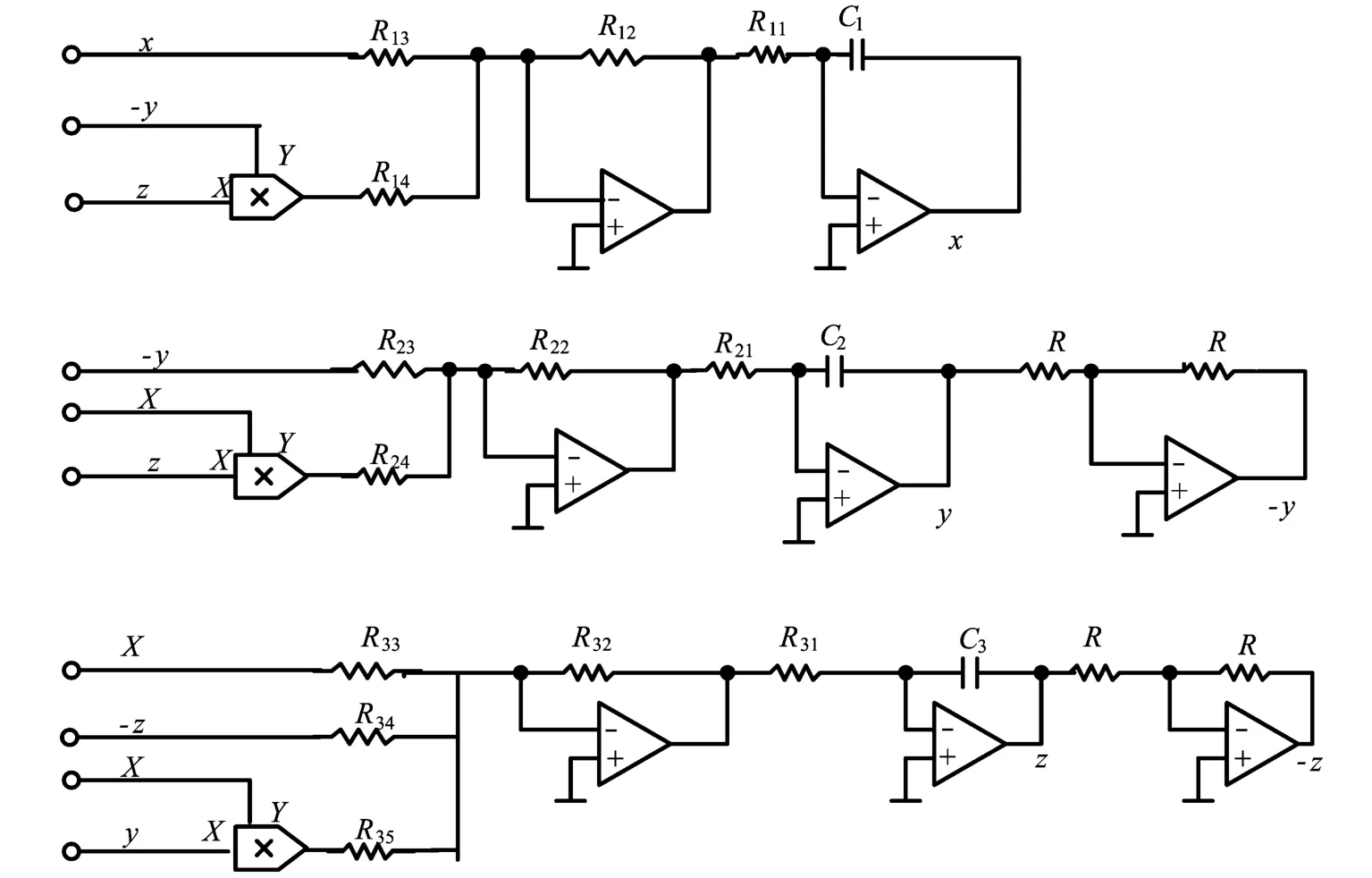
图4 三维四翼混沌系统的电路结构图

电路相应数学模型通过线性变换，可得：

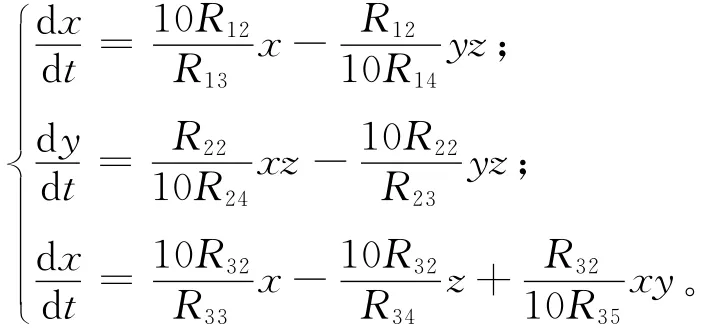
当a＝3、b＝8、c＝4、k＝1、d＝2时，设R＝R11＝R21＝R31＝R12＝R22＝R32＝10kΩ，得到R13＝33.3kΩ，R14＝1kΩ，R23＝12.5kΩ，R24＝0.25kΩ，R33＝100kΩ，R34＝50kΩ，R35＝1kΩ。

通过上述参数的设置，在示波器上观察到的混沌吸引子相图和仿真结果一致，如图5所示。

图5 实验中观察到的混沌吸引子

4 结束语

本文在文献［8］伪四翼混沌系统的基础上，通过引入变量x的正反馈，构造了一个新的三维四翼混沌系统。理论分析和数值仿真证明在平衡点S2、S3处发生了Hopf分岔行为。Lyapunov指数和分岔图证明系统轨迹经历了不动点、单周期、双周期、三周期及混沌吸引子等，验证了混沌系统动力学特性。硬件电路实验结果验证了三维四翼混沌系统的四翼混沌吸引子存在性。

［1］ Chen G，Lai D.Feedback control of Lyapunov exponents from discrete－time dynamical systems［J］.Int J Bifurcation and Chaos，1996，6（7）：1341－1349.

［2］ Qian Q C，Chen Z Q，Yuan Z Z.Video compression and encryption based－on multiple chaotic systems［J］.International Journal of Innovative Computing，Information and Control，2010，6（1）：315－322.

［3］ 包伯成，王其红，许建平.基于忆阻元件的五阶混沌电路研究［J］.电路与系统学报，2011，16（2）：66－70.

［4］ Wu W J，Chen Z Q，Yuan Z Z.A computer－assisted proof for the existence of horseshoe in a novel chaotic system［J］.Chaos Solitons and Fractals，2009，41：2756－2761.

［5］ Dong E Z，Chen Z P，Chen Z Q，et al.A novel four－wing chaotic attractor generated from a three－dimensional quadratic autonomous system［J］.Chinese Physics B，2009，18（7）：2680－2689.

［6］ Grassi G，Severance F L，Miller D A.Multi－wing hyperchaotic attractors from coupled Lorenz system［J］.Chaos Solitons and Fractals，2009，41（1）：284－291.

［7］ 袁开艳，李丽梅.基于CNN的混沌参数扩频调制数字保密通信系统［J］.合肥工业大学学报：自然科学版，2012，35（4）：489－492.

［8］ Liu W B，Chen G.Can a three－dimensional smooth autonomous quadratic chaotic system generate a single four－scroll attractor？［J］.International Journal of Bifurcation and Chaos，2004，14，（4）：1395－1403

［9］ Chen Z Q，Yang Y，Yuan Z Z.A single three－wing or fourwing chaotic attractor generated from a three－dimensional smooth quadratic autonomous system［J］.Chaos Solitons and Fractals，2008，38：1187－1196.

［10］ 王繁珍，齐国元，陈增强，等.一个四翼混沌吸引子［J］.物理学报，2007，56（6）：3137－3144.