混合遗传算法在WSNs定位中的应用*
2014-12-31刘彦隆吕显朋王相国
刘彦隆,吕显朋,王相国
(太原理工大学信息工程学院,山西太原 030024)
0 引言
无线传感器网络(WSNs)在环境监测、军事国防、抢险救灾等很多的领域中具有广阔的应用前景,而网络的节点定位或者是监测目标定位是WSNs应用的支撑,节点定位又是外部目标定位的基础[1],所以,节点定位就显得异常重要。节点定位分为基于距离和基于估计距离的定位,后者受复杂环境对信号传输影响低,并且硬件成本较少,能耗小,非常适合 WSNs的应用[2]。
Dragos Niculescu利用GPS和距离矢量路由思想提出的DV—Hop算法就是基于估计距离的定位[3]。DV—Hop没有直接测量距离,是利用交换距离矢量信息和网络连通度,将距离巧妙转换成估计的距离,所以,DV—Hop不需要高装备的测距单元,尤其在各项同性网络里性能良好[2]。
本文针对DV—Hop第三阶段利用最小二乘法处理非线性约束问题时精确度较差的问题,提出了基于遗传算法(GA)单纯形法的混合GA,经过实验仿真,混合算法具有良好的性能,是一种适合WSNs的可行算法。
1 相关理论
DV—Hop定位算法的第三阶段[4]:将第一,二阶段计算出的未知节点o(x,y)到信标节点A1(x1,y1),A2(x2,y2),…,An(xn,yn)跳段的距离d1,d2,…,dn,利用极大似然估计的方法计算(x,y);由两点间的距离公式,可得
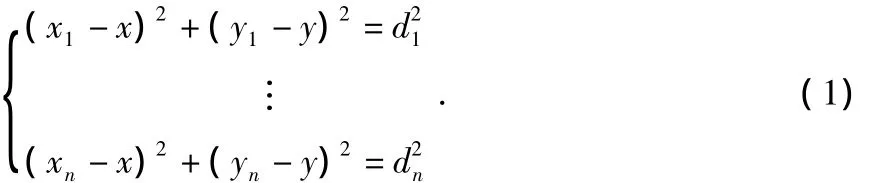
对式(1)化简整理可得线性方程AX=b,其中
利用最小二乘法

其中,dn存在于b的各个元素中,使得用(ATA)-1ATb求出的坐标受制于dn的精度,因此,用最小二乘法求解虽然简便,却极大地降低了解的准确度,因此,可以将问题的求解转化为约束优化的问题[6]。
假设信标节点A1,A2…,An到o的真实距离为r1,r2,…,rn;ε1,ε2,…,εn为传感器的测距误差范围。式(1)可化为

则问题可化为求解

因此,把DV—Hop第三阶段转化为求解约束性优化问题,f(x,y)的求解即为非线性优化问题,众多学者提出了用人工蜂群[7](收敛速度快)、约束粒子群[6](收敛速度快)、GA[8,9](解决全局的优化问题)、模拟退火算法[10,11](有效地避免寻得局部最优解)、差分进化的算法[12](算法复杂度低)等求解优化问题。
本文提出的用GA+单纯形法的混合遗传性算法优化DV—Hop算法,不仅保留了GA的优势,单纯形法和最优个体保优的原则也避免了GA的弊端,得到了更加精确地定位。
2 混合GA求解约束问题
2.1 算法的原理
优胜劣汰与适者生存的生物进化规律存在于各阶系统中,进化过程就是具有较好健壮性自适应的过程,受生物进化的启发,Holland J提出了GA,它非常适合组合和优化问题中全局最优解的求解[13],能大概率地获得最优解,而且在数学上较容易实现[14]。
GA的基本程序:算法不断迭代和更新假设的群体,并且在每次迭代中,用适应度函数计算评价所有个体,以概率的方法选择适应度较高的个体通过选择、交叉和变异等遗传算子产生新群体[14]。
但是GA存在运算时间长、局部搜索能力差等固有的缺陷[14],因此,本文对GA采用了最优个体保优的原则的改进,改善运算时间长的弊端;并且采用了在局部搜索能力领域具有较强先验性的单纯形算法与GA结合的混合GA。
单纯形法通过相应的一系列转换,把各种非标准形式的问题变化成标准形式,从而求解;因此,它对含有很多个约束条件的非标准形式的线性问题的求解非常有效。
2.2 求解约束问题
用GA+单纯形法的混合GA求解f(x,y),设计其适应度函数,要使代价函数f(x,y)最小,采用最大系数法,即

式中Cmax为最大系数。

3 一种基于GA+单纯形法的DV—Hop定位算法改进
假设有N个节点存在于一个WSNs中,其中包含M个信标节点,利用M个信标节点去定位N-M个未知节点,随着定位的进行,未知节点转换为已知坐标的新的信标节点协助定位,但只有这M个信标节点的位置信息是没有误差的精确值,信标节点与未知节点,未知节点与未知节点之间允许有一定的测距误差,两节点之间的距离不能超过WSNs测距的半径;并假设WSNs中不存在孤立点,孤立点问题属于WSNs布局问题[6],本文不讨论。
综上,算法基本流程为:
1)计信标节点个数t(初始时t=M),在Mx(初始时Mx=N-M)个未知节点里,找出邻居信标节点最多的未知节点Nx开始以下步骤。
2)随机的产生群体规模为n的初始群体。
3)将适应度函数F(x,y)=f'(x,y)+p(x,y)进行指数定标,则新的适应度函数为fitness=ekF(x,y);利用适应度函数,计算群体中所有个体的适应度。
4)最优个体的保优原则,把所有个体按适应度高低排列,适应度最高的5个个体跳到第6步,剩下的n-5个个体组成群体p继续执行第5步。
5)GA的操作,产生新的一代Ps:
a.选择(复制):本文采用轮盘赌的方法;
b.交叉(重组):本文采用二点交叉的方法;
c.突变:选择一个或多个基因位,按变异概率pm做相应的变动;
d.更新:p←ps。
6)第4步最优的5个个体与第5步遗传操作后的个体数为n-5的群体ps组成新群体。
7)单纯形法,在生成的新群体里以一定的概率选择个体进行单纯形法,计算后的新个体代替原个体。
8)若群体的性能已经满足性能要求,或达到了迭代次数(本文选用后者),执行第9步;否则,跳到第3步。
9)由上可得Nx的位置坐标,把Nx看做信标节点,t←t+1;t<N时,跳到第1步,t=N时,WSNs中所有未知节点都被定位,算法结束。
算法第3步,将适应度函数F(x,y)进行指数定标,形成新的适应度函数fitness,可以扩大个体间的竞争,但又不违反适应度函数基本性原则;算法第4步采用了最优个体的保优原则,最优的个体不经历遗传算子运算,直接进行下一步,降低算法运行的时间,能适当减少迭代的次数,能够实现高效迭代寻优;算法第7步,采用了单纯形法,显然是作为GA局部搜索的算子,这样,可以利用单纯形法局部搜索能力强的优势加强GA的局部搜索能力。
4 仿真实验与评价
4.1 仿真场景与参数设置
在[100,100]m的区域内,用 Matlab分别对传统 DV—Hop定位算法,GA DV—Hop定位算法与GA+单纯形法的DV—Hop定位算法进行仿真,为了使算法的仿真结果更加真实,每一次仿真开始前,由参数(WSNs的连通度与信标节点的密度)生成网络的拓扑结构;在所有的节点中随机生成信标节点,并且信标节点均匀散布在区域内(要比随机散布性能好)[15];在每一种条件下仿真多次,之后分别对其结果求其平均值;只讨论各项同性的WSNs。
用网络的覆盖程度与平均定位误差评价定位性能的优劣[16],定位误差
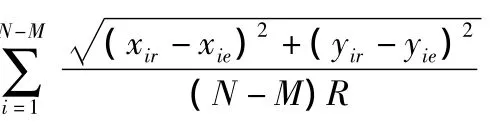
GA+单纯形法需要设定参数,本文采用二进制编码,编码长度l=14,群体规模M=50,交叉概率pc=0.9,变异概率pm=0.02,迭代次数tm=200;本文采用了Nelder-mead单纯形法,其中,需要设定的参数为反射因子α、扩张因子β、收缩因子 γ,各因子取 α =1,β =0.5,γ =2,经仿真实验,如上参数的设置,具有良好的定位性能。
4.2 结果分析
1)网络连通度对定位精度的影响
在区域内布置250个节点,假设信标节点的个数为10,图1为传统 DV—Hop定位算法、GA DV—Hop定位算法与GA+单纯形法的DV—Hop定位算法的仿真图,由图可知,当连通度小于10时,3种算法的误差都降低,且幅度较大,而GA定位性能明显优于传统DV—Hop定位算法,GA+单纯形法的定位算法误差又小于GA,这是由于单纯形法弥补了GA的一些弊端;当连通度大于10时,由于估计值为相隔的跳数,随着网络连通度增加,把相隔的跳数看做估计值估计距离就不精确了,因此,3种定位算法的性能都有所恶化,但是GA+单纯形法的DV—Hop算法精确度明显高于另外2种算法,而且其恶化幅度也较缓慢。

图1 网络连通度对定位精度的影响Fig 1 Impacts of network connectivity on localization precision
2)信标节点数目对定位精度的影响
在区域布置250个节点,信标节点比例由0.02~0.12,图2为在各向同性网络中信标节点比例对3种算法的影响,由图可知,随着信标节点比例的增加,3种定位算法的性能都有所改善,误差减小明显,这是由于随着信标节点比例的增加,可利用的定位节点的数目增加,网络的可知性增强,而且在信标节点的各个比例下,GA+单纯形法的定位算法定位精度始终高于另外2种算法。

图2 信标节点数目对定位精度的影响Fig 2 Impacts of beacon node number on localization precision
3)信标节点数目对网络覆盖率的影响
由图3可知,随着信标节点比例的增加,3种定位算法的网络覆盖程度都有所加大,而且GA DV—Hop定位精确性优于传统DV—Hop算法,而GA+单纯形法的定位性能又显著优于GA DV—Hop定位,在信标节点比例较小的时候,网络覆盖程度增大的幅度较大,3种算法覆盖程度的差距也较大,信标节点的比例增加到一定的程度,网络覆盖程度增加的也较为缓慢,算法之间的差距也减小,趋于平稳。

图3 信标节点数目对网络覆盖率的影响Fig 3 Impacts of beacon node number on network coverage rate
5 结论
GA由于本身的特性适合对传统的DV—Hop定位得出的位置进行修正,本文提出一种基于GA+单纯形法的混合GA对传统的DV—Hop定位的第三阶段进行优化,计算量与能量没有过多增加,却保留了GA的优势,也利用了单纯较强的领域先验性弥补了GA的一些固有缺陷,仿真结果表明:改进算法在各项同性的WSNs中比其它定位算法有更高的定位精度与网络覆盖率,非常适合于WSNs的定位,是一种行之有效的改进算法。
[1]张西红,周 顺,陈立云.无线传感网技术及其军事应用[M].北京:国防工业出版社,2010.
[2]景 博,张 劼,孙 勇.智能网络传感器与无线传感器网络[M].北京:国防工业出版社,2011.
[3]谢晓松,程良伦.无线传感器网络基于移动信标动态选择的定位算法[J].传感器与微系统,2011,30(1):123-130.
[4]马润泽,余志军,刘海涛.一种距离无关的无线传感器网络定位算法[J].传感器与微系统,2011,30(11):131-134.
[5]孙利民,李建中,陈 渝.无线传感器网络[M].北京:清华大学出版社,2005.
[6]欧阳丹彤,何金胜,白洪涛.一种约束粒子群优化的无线传感器网络节点定位算法[J].计算机科学,2011,38(7):46-49.
[7]李牧东,熊 伟,郭 龙.基于人工蜂群算法的 DV—Hop定位改进[J].计算机科学,2013,40(1):33-36.
[8]陈 坤,李 莉,李继云.基于遗传算法的井下无线传感器网络节点定位研究[J].煤炭工程,2010(10):120-122.
[9]邓 力.基于 遗传算法 WSNs节点定位算法研究[J].计算机仿真,2011,28(9):161-164.
[10]赵仕俊,孙美玲,唐懿芳.基于遗传模拟退火算法的无线传感器网络定位算法[J].计算机应用与软件,2009,26(10):189-192.
[11]范玉红,彭 宏,朱陈良.一种基于遗传模拟退火算法和RSSI的无线传感器网络定位算[J].西安大学学报,2010,29(6):51-54.
[12]Chehri A,Fortier P,Tardif P M.Geolocation with wireless sensor networks using nonlinear optimization[C]//Proceedings of International Journal of Computer Science and Network Security(IJCSNS),2008:1452154.
[13]柴玉梅,张坤丽.人工智能[M].北京:机械工业出版社,2012.
[14]张清华.人工智能技术及应用[M].北京:中国石化出版社,2011.
[15]郭绍永,谈 冉.遗传算法在无线传感器网络中的应用[J].传感器与仪器仪表,2009,25(4-1):125-127.
[16]杨石磊,樊晓平,刘少强.一种改进的无线传感器网络 DV—Hop定位算法[J].计算机测量与控制,2008,16(9):1356-1357.
