基于区域权函数理论的多电极电磁流量计电极设计*
2014-12-31赵宇洋LUCASLEEUNGCULSATIEN
赵宇洋,张 涛,LUCAS G,LEEUNGCULSATIEN T
(1.天津大学电气与自动化工程学院天津市过程检测与控制重点实验室,天津 300072;2.School of Computing and Engineering,University of Huddersfield,HD1 3DH UK)
0 引言
电磁流量计根据法拉第电磁感应定律原理制成,多电极电磁流量计(MEMF)针对非轴对称流测量应运而生,以解决两电极电磁流量计的弊端。Horner B[1]提出以层析成像为基础的六电极电磁流量计,证明多电极流量计对速度分布不敏感,但未给出局部速度信息。Teshima T[2]设计出旋转磁场下的多电极电磁流量计。此外,Bernier R[3]将多电极测量方法应用于两相流测量当中,Gladden L也曾做过有益的尝试[4]。本文设计了一种多电极电磁流量计,基于区域权函数理论实现流场速度分布测量,针对被测对象特点,采用不锈钢平头电极,并验证了该设计对于单相非轴对称流和固—液两相流倾斜管测量具有较高的精度与可靠性。
1 多电极电磁流量计设计
1.1 多电极测量与区域权函数
多电极电磁流量计由流动截面处不同弦位置处的感应电势差,实现速度分布和体积流量测量。徐立军[5]针对多电极阵列的数量和尺寸进行了详细的仿真研究,得出16电极等圆心角分布为最优配置的结论。Shercliff权函数理论[6]作为电磁流量计的重要理论依据,指出流动截面上各个流体质点都影响感应电动势的数值,表明由于权函数分布不均匀导致两电极电磁流量计对流速分布轴对称比较敏感。
本文选取16电极测量方式[7],其电极均匀分布在圆周上的任意位置,成对测量管道截面的弦端电压,并不都沿直径分布,因此,提出区域权函数概念,将质点的速度对两电极上感应电动势的影响引申为区域内平均速度对各对电极间感应电动势的影响。
区域权函数的研究对象不再是单独的流动质点,而是不同区域内的轴向平均速度,如图1所示,将流动截面划分为I=7 个区域,电极 eGND和 eGND'接地,电极对 elel'~e7e7'分布在与直径平行的弦上,各对电极间感应电动势大小表示为

其中,Uj为第j对电极测量的感应电压,B为截面处磁感应强度,a为管道半径,¯vi为各区域内的平均流速,Ai为各区域面积,权函数wij表示不同区域的流体对各感应电压值的贡献大小。

图1 多电极电磁流量计电极分布图Fig 1 Electrode distribution diagram of multi-electrode electromagnetic flow meter
仿真表明:1)平行布置各区域更有利于反映管道内速度剖面的变化;2)测量电极位于各区域在y方向上的中心处时,可以获得最强的感应电动势信号,提高计算和测量精度。
根据公式(1),多电极电磁流量计通过传感器获取测量截面不同位置的感应电压值,便可得到图1中各个区域内的轴向平均速度,并计算导电流体的体积流量。多电极电磁流量计测得单相导电流体积流量为

固—液两相流中导电相体积流量为Qw,tp

其中,αs,i为第i个区域内固体的相含率。文中实验选取六电极探针[8]作测量固相含率,在实际应用中还可采用电阻层析成像技术(ERT)等来测量局部固相含率αs,i的值。
1.2 电极设计
电磁流量计传感器的电极安装在与磁场方向垂直的测量管壁上,将被测介质切割磁力线所产生的电势信号引出。因此,电极能否可靠检测流量信号,对流量计性能至关重要。电极与被测流体介质直接接触,首先,要考虑材质的抗腐蚀性和表面效应,电磁流量计只允许电极极低的腐蚀速率甚至不允许有腐蚀;其次,电极必须是非磁性导电材料,不会对工作磁场造成干扰;另外,电极材料的选定还需参考被测介质在其他设备的实际应用情况和以往经验,结合现场条件而确定。
多电极电磁流量计旨在解决速度分布非轴对称流体的测量问题,针对单相水流和固—水两相流应用对象,电极材料选用316L不锈钢和黄铜,两者的相对磁导率约等于1,表明电极拾取的感应电动势不因电极的导磁性受到影响,只随流体速度变化而变化。
图2(a)为内插式圆头电极,图2(b)为平头电极,基于圆头电极改进得来,针对固—水两相流信号特点,增大了电极面积,减小电极流场中的凸台。电极安装在测量管时需要利用不锈钢和橡胶垫圈进行密封,并使用测力扳手按一定力矩安装。

图2 电极2D设计图Fig 2 Electrode 2D design
在多相流测量,特别是本文研究的固—液两相流的测量中,非导电固体颗粒对电极的碰撞会带来很大的感应电压信号误差,并对转换器电路设计带来难度[7]。
如图3所示,流量计传感器采集的7路电压信号中,由于颗粒碰触电极产生了尖锐的脉冲信号。经过信号检测电路的放大后,脉冲干扰会给感应电压的测量引入很大误差。为避免上述影响,平头电极b的设计尽可能减少了在管壁内突出部分的尺寸,只有电极表面暴露在被测流体中并与之接触。实验证明:采用平头设计方案显著改善了电压信号中的脉冲干扰。

图3 颗粒碰撞引起的干扰电压Fig 3 Interference voltage caused by impact of particles
2 电极对于非对称速度测量实验
2.1 实验系统
实验在英国Huddersfield大学低压固—水两相流装置上进行,实验装置分为介质源、计量管段、可调角度的实验管段及计算机控制系统4个部分。
如图4所示,实验液相介质为水,涡轮标准表计量的流速范围为0.7~17.6m3/h,精度为 ±0.05%。固相介质为平均直径5 mm、平均密度为1340.8 kg·m-3的绝缘颗粒。在固—液两相流实验中,固体颗粒与水在混合罐中充分搅拌,由固体泵将两相混合物送入实验管段。

图4 实验装置示意图Fig 4 Diagram of experimental device
2.2 速度分布测量实验
在设计阶段,利用皮托管测量计算各区域中的速度分布值。皮托管作为侵入式测量方法会对流体流动引入干扰,但在目前有限的技术条件下,仍可作为局部轴向平均速度分布的标准值来衡量流量计的性能。皮托管沿管道截面16个径向方向得到80个坐标点的速度值。因自身几何尺寸影响,在管壁附近无法实现多次测量,区域1和7内只包含一个测量点。皮托管测得全部速度值后,将各区域内所包含的测量点速度求平均值,作为该区域内的轴向平均速度参考值。
电极性能研究实验在图4所示单相流水装置中完成,流量计安装在阀门下游,更换不同电极进行测量,图5中速度分布结果表明电极材质、形状对测量影响严重。图中,“设计1”表示黄铜圆头电极,“设计2”表示不锈钢圆头电极,“设计3”表示黄铜平头电极,“设计4”表示不锈钢平头电极。
如图5所示,“设计4”即图2(b)所示的不锈钢电极,速度分布测量结果与阀门曲线较吻合,并且与皮托管参考值相对误差较小,因此,在样机设计中选取该电极设计方案。另外,需要注意:在长时间实验后,黄铜电极表面出现了轻微腐蚀痕迹,将引入严重的测量噪声,而不锈钢电极抗腐蚀性良好,适用于实际测量。
虽然图5中平均速度值在测量管顶部和底部区域1和7处出现最大误差,但原因是:由于皮托管测量原理的限制和在区域1和7内只有一个测量点,造成速度参考值精度较低;另外,由Shercliff权函数理论可知,与电极距离越近权函数数值越高,区域1和7的权函数w1j和w7j数值远高于其他,因此,电压U1和U7测量值的微小扰动也会带来速度测量的较大差异。
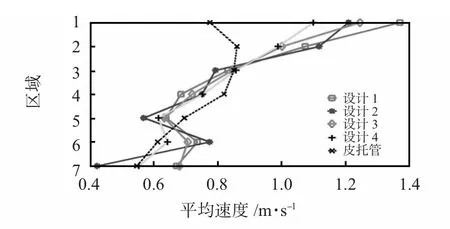
图5 不同电极设计对速度分布的测量Fig 5 Velocity distribution measured by different electrode design
3 单相非轴对称流与固—液两相流实验
单相非轴对称流实验中,将多电极电磁流量计安装在阀门下游,通过控制阀门开度改变管道中的体积流量,电磁流量计与涡轮流量计标准值的相对误差如表1所示。

表1 单相非轴对称体积流量测量相对误差Tab 1 Relative errors of non-axisymmetric single phase volume flow rate measurement
表1中电磁流量计在未经仪表系数校正的前提下,对体积流量测量的相对误差在±1.0%范围内,具备较高测量精度。
本文阐述的两相流实验中,多电极电磁流量计安装在30°倾斜管段中,分别在fm1~fm6不同固相含率值下进行实验,多电极电磁流量计对水相体积流量的测量值与称重装置标称值的相对误差如表2所示。

表2 固—液两相流倾斜管水相体积流量相对误差Tab 2 Relative errors of water phase flow of inclined pipe solid-liquid two phase flow
由公式(3)可知,局部固相含率αs,i的测量精度有限,使得电磁流量计在水相体积流量测量的误差波动较严重。
4 结论
本文介绍了基于区域权函数的多电极电磁流量计,针对被测对象特性着重讨论了不同电极设计方案。实验表明:对于单相非轴对称流,采用不锈钢平头电极的多电极电磁流量计具备较高精度;对于固—液两相流,该流量计可以提供管道测量截面的局部轴向速度信息,结合高精度的固相含率测量手段,也将提高多电极电磁流量计的体积流量测量精度。
[1]Horner B,Mesch F,Trachtler A.A multi-sensor induction flowmeter reducing errors due to non-axisymmetric flow profiles[J].Measurement Science and Technology,1996,7:354-360.
[2]Teshima T,Honda S,Tomita Y.Electromagnetic flowmeter with multiple poles and electrodes[C]//Instrumentation and Measurement Technology Conference,Hamamatsu,Japan,1994:1221-1224.
[3]Bernier R,Brennen C.Use of the electromagnetic flowmeter in a two-phase flow[J].International Journal of Multiphase Flow,1983,9(3):251-257.
[4]Sankey M,Yang Z,Gladden L,et al.Sprite MRI of bubbly flow in a horizontal pipe[J].Journal of Magnetic Resonance,2009,199(2):126-135.
[5]徐立军,王 亚,乔旭彤,等.多对电极电磁流量计传感器电极阵列设计[J].仪器仪表学报,2003,24:335-339.
[6]Shercliff J A.The theory of electromagnetic flow-measurement[M].Cambridge,UK:Cambridge University Press,1962.
[7]赵宇洋,张 涛,Lucas G.多电极电磁流量计转换器设计[J].传感器与微系统,2012,31(6):87-93.
[8]Lucas G P,Cory J,Waterfall R C,et al.Measurement of the solids volume fraction and velocity distributions in solids-liquid flows using dual-plane electrical resistance tomography[J].Flow Measurement and Instrumentation,1999,10:249-258.
