钨合金长杆体高速撞击薄钢板的跳飞研究

董玉财，杜忠华，刘荣忠，刘 杰，夏龙祥，汪得功

（1.南京理工大学 机械工程学院，南京210094；2.中国兵器工业集团第五三研究所，济南250031）

弹丸由于能量不足或者着角过大无法持续地侵入到钢甲中，且靶板抗力的方向始终没扫过弹丸的质心，因此弹丸就会在翻转力矩作用下发生跳飞。国内对跳飞研究的文献相对很少，还未见相关的理论研究文献。吴荣波等［1］利用 ANSYS／LS－DYNA软件对弹丸以不同入射角侵彻半无限厚土进行了数值模拟研究，得出入射角不大于75°不能发生跳飞的结论。荣光等［2］利用数值仿真分析了高速撞击过程中不同入射角的异型弹芯的斜侵彻运动，得到了入射角与侵彻深度的变化规律。国外，Jonas和Zukas［3］等利用X光摄影试验及仿真等方法对长杆式弹丸的跳飞现象进行了研究，他们认为跳飞发生的过程是在弹与靶撞击接触点形成一个塑性的铰链（视该接触点相对于靶板静止），弹杆绕该接触点沿与靶板接触表面发生向靶板外侧的偏转。Tate，Rosenberg，Steven B等［4－6］分别建立了不同的跳飞模型，但模型均是针对半无限厚靶板而建立，因此均未考虑到靶板厚度对跳飞角的影响。本文针对薄装甲钢靶板的跳飞现象，通过数值仿真结果结合已有模型的特点进行修正，并进行了相应试验，对所得模型计算结果和数值仿真结果进行了验证。

1 数值仿真研究

在1 300～1 700m／s初速范围，对杆式弹斜侵彻薄均质装甲钢靶板跳飞的过程进行数值模拟，对不同厚度（6～14mm）的靶板的跳飞角进行探究。为了减少数值模拟初期的盲目性，降低一定工作量，通过文献［4－6］中的模型进行初步计算，除文献模型中涉及到的材料及结构参数外，弹体对靶板的初始侵彻速度vx［7］表达式为

式中：v为弹体的撞击速度为靶板的密度，ρp为弹体的密度；Rt为靶板的抗力，Yp为弹体的动态屈服强度；着速为1 560m／s时vx＝620.2m／s，通过Tate模型、Rosenberg模型、Steven B模型计算得出的跳飞角分别为82.3°，77.3°，79.1°。

1.1 数值计算模型

采用有限元软件LS－DYNA计算93W合金弹体斜侵彻603装甲钢靶板。弹体和靶板单元类型均为SOLID160，网格单元采用八节点六面体。弹体与靶板接触方式为ERODING＿SURFACE＿TO＿SURFACE，弹体及靶板均采用Johnson－Cook材料模型和Gruneisen状态方程。二者之间采用侵蚀算法，并与失效准则连用，当单元的有效塑性应变达到失效应变或者单元压力达到最小压力时，则单元失效［8］，计算中失效的单元将被删除。由于所建模型具有对称性，弹体和靶板均取原型的1／2，弹体的平均直径为6mm，长为110mm，靶板为200mm×20mm×厚度（6～14mm）的长方体，对靶板侧表面施加全自由度约束和非反射边界约束（为了便于计算，取靶板宽度为弹径尺寸的3倍左右，故在文中为20mm），由非反射约束应力波在侧边界进行透射，在数值模拟的计算过程中，则可以认为靶板的侧边界为半无限的结构状态，本文研究并未考虑靶板厚度的侧边界效应影响。对弹体直接作用的靶板区域进行网格加密，其余部分网格划分相对稀疏。具体材料参数如表1所示。表中，ρ，E，μ分别为材料的密度、杨氏模量、泊松比；A为与材料屈服极限相关的常数；B，C，n为与材料的应变硬化及应变率相关的系数；m为温度系数；Tmelt，Troom分别为材料的熔点及室温，K为调节系数。

表1 Johnson－Cook材料参数

Johnson－Cook模型的应力－应变关系为：σy＝［A＋B）n］（1＋Cl）（1－T＊m），式中：A，B，C，n为材料常数；为有效塑性应变为有效塑性应变率为相当温度（其中T为实际温度，Troom为室温，Tmelt为熔点温度）；m为常数，计算时采用Gruneisen状态方程。对可压缩材料，压力的表达式为

式中：ρ0为初始密度；U为内能，μ＝ρ／ρ0－1，ρ为当前密度；C，S，γ0，a为材料参数。

1.2 数值模拟结果及分析

在数值模拟过程中，通过每次改变0.5°着角来获得不同厚度靶板的跳飞角。着速1 560m／s时，6mm厚靶板趋近跳飞角数值模拟的侵彻过程如图1、图2所示。

如图1所示，在着角84.5°的侵彻过程中，弹体与靶板接触处形成类似Steven B［6］提及的塑性铰链，铰连接点并非如Steven B模型中认为的该连接点是固定的，而是在90μs内随着侵彻的进行沿着靶板表面向前推动。90μs后，弹体的末端部在靶板抗力与前端拉应力的联合作用下与主弹体在铰接点断裂分离，并继续对靶板进行侵彻，并最终穿透6mm的靶板，靶板后部的残余弹体质量接近于零，上述现象与Daneshjou K［9］研究涉及的相关内容较为吻合。整个过程尽管前端大部分弹体撞击靶板后跳飞出靶面，后端剩余弹体仍然穿透靶板，发生不完全的跳飞。本文研究需要得出的是完全跳飞时靶板角度，因此，将着角增加0.5°进行下一步的模拟，如图2所示。

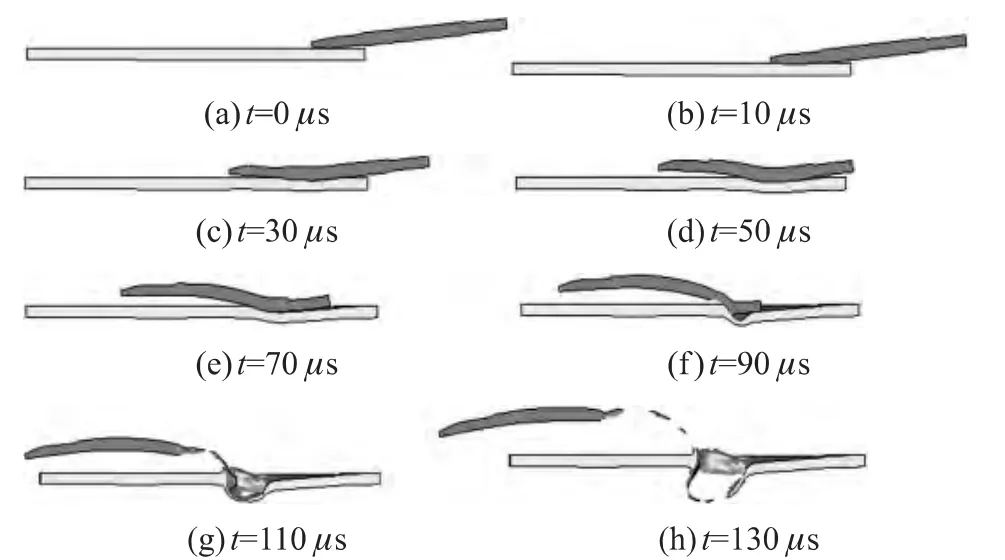
图1 着角为84.5°的侵彻过程

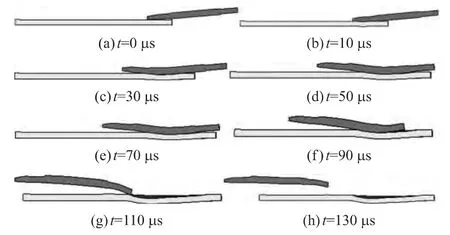
图2 着角为85°的侵彻过程

由图2可知，着角增至85°，在侵彻的整个过程中弹体没有发生明显破碎。此过程中，仅在与靶板接触部位的弹体绕铰接点产生了偏转，在距弹体末端约13mm处最后出现了不可恢复性的弯曲变形，最后弹体几乎与靶板平面平行飞出，这种现象与Daneshjou K仿真结果较为一致。由此过程得出1 560m／s速度时，6mm靶板的跳飞角为84.75°（取产生跳飞的最小着角与没有产生跳飞的最大着角的平均值）。由于仿真采用着角间隔为0.5°，由该方法自身引起的误差应在0.5°内。

通过采用以上的方法，数值模拟得到1 560m／s时，6～14mm靶板的跳飞角。弹坑的图像如图3所示。

图3 8～14mm靶板跳飞后靶板的弹坑

靶板厚度以2mm均匀增加，跳飞角θcrit随靶板厚度b的变化如图4所示。从图4中的曲线发现，跳飞角的降低存在逐渐减缓的趋势，该过程说明随着靶板厚度的增加，着角改变对跳飞的影响呈强化趋势，靶板的厚度因素呈弱化趋势。6～10mm厚靶板的跳飞角在82°～84.75°之间，更接近于Tate模型的计算结果82.3°。但3种模型均是针对半无限靶板建立的，忽略了靶板厚度因素的影响，而Tate模型的计算结果实际上更接近于有限厚靶板。12～14mm厚靶板的跳飞角在80.75°～81.25°之间，更接近于Steven B模型计算的结果79.1°，并且随着靶板厚度的增加跳飞角下降趋势变缓，其对半无限靶板预测是相对准确的，而Rosenberg模型和Steven B模型对半无限靶板计算结果准确性的比较需做进一步的研究。

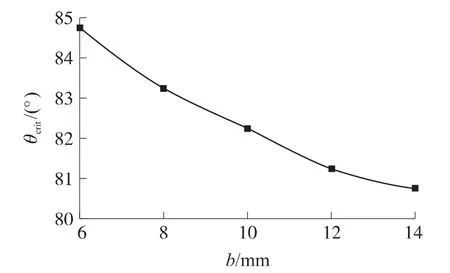
图4 跳飞角随靶板厚度的变化

2 理论模型

2.1 已建立的模型

Tate［4］采用圆柱杆截面的弹芯建立起早期的杆式弹的跳飞模型，得到了跳飞的表达式，当入射角超过此θcrit角时则发生跳飞现象。其模型为

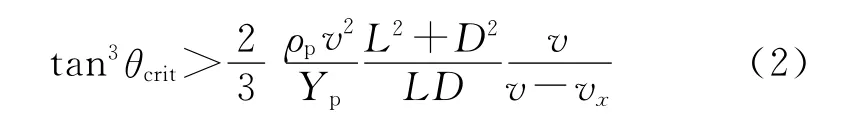
式中：ρp为弹体密度；v为弹体的撞击速度；Yp为弹体的动态屈服强度；L，D分别为杆体的长度和直径；vx为弹体着靶时初始侵彻速度。

Rosenberg［5］假设靶板抗力仅作用在侵入到靶板的这部分质量的弹体上，而不是全部剩余弹体上，抗力作用在弹体的头部位置使其在横向发生偏离，而不是产生对弹体质心的旋转力矩。此阐述与其他学者提出的跳飞过程中形成的塑性铰链的机理是一致的，其模型为

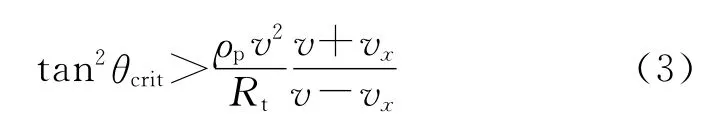
式中：Rt为靶板的抗力，其余参数同Tate模型。

Steven B［6］等人提出了完全塑性铰链的数学模型，并进行简化，其模型为

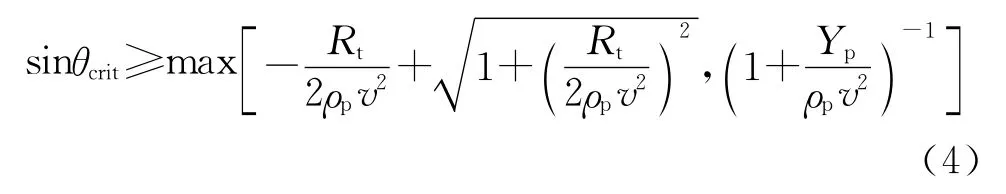
2.2 修正模型

通过上文所得的仿真数据，结合Tate模型的特点，对该模型加入靶板厚度参量进行修正，来实现对薄装甲钢靶跳飞角的预测。将Tate模型右侧乘以一个关于靶板厚度的未知系数，将结果数据及其它参量带入，将其进行左右两侧同时开三次方处理（由于在该靶板厚度区域跳飞角的正切值是单调函数）。可通过处理等式的方式反求得出不同厚度下未知系数的大小，然后利用Matlab程序二阶函数多项式进行拟合，即可得出在一定靶板厚度范围内发生跳飞模型的表达式：

在1 560m／s速度下，数值模拟及修正后模型的计算结果如图5所示。

图5 跳飞角正切值与靶板厚度的关系

3 检验验证

3.1 仿真检验

为了检验该修正模型在其它速度下的适应性，分别在1 300m／s，1 500m／s，1 700m／s速度下，通过本文采用的数值模拟方法得到6mm、10mm、14mm等厚度靶板的跳飞角。数值模拟结果与修正模型计算结果的对比如图6所示。由图6可知，靶厚为6mm、10mm时，二者的一致性相对更好，且各厚度靶板数值模拟值均略大于修正模型的计算值，其原因可能是数值模拟中材料参数或计算初始侵彻速度vx的模型存在偏差。在上述的计算条件下，修正模型与数值模拟二者所得跳飞角的值相差均不大于0.93°。

图6 修正模型计算结果与数值模拟跳飞角的对比

3.2 试验检验

试验场地的基本布置如图7所示，采用25mm弹道炮进行发射，利用双层锡箔附在纸靶上进行测速。如图8所示的特制靶架通过两侧的4个螺栓连接对靶板进行固定，且通过在螺母下增减垫片调整靶板的倾斜角度。试验弹丸采用25mm长杆式穿甲弹，弹丸结构如图9所示，弹芯为93W合金，长为110mm。

图7 试验布置情况

图8 倾斜靶固定装置及收弹器

图9 试验弹丸

在进行靶板试验前，先进行了几发弹丸的试速试验，确定1 560m／s着速时的装药量约为145g，且该速度下垂直侵彻时可穿透100mm的装甲钢靶板，各方案均采用该装药量，弹丸的质量约为99g，结果见图10。图10中着速的差异是由弹丸的发射、飞行及装配等多种因素所造成的。

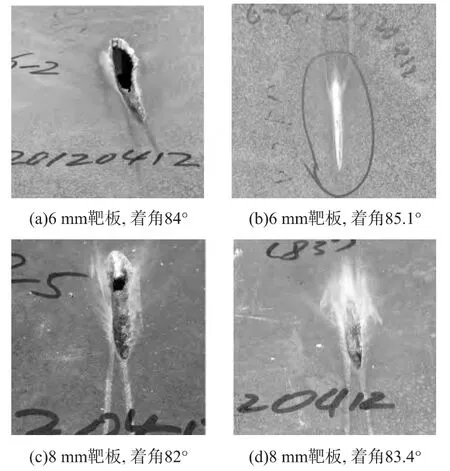
图10 试验弹坑

图10 （a）、10（b）分别为着角84°、85.1°，6mm靶板试验后的靶况；图10（c）、10（d）分别为着角82°、83.4°，8mm靶板试验后的靶况，具体试验数据如表2所示。表中，θ为着角，v为着速。结合前文及表2，6mm、8mm厚装甲钢靶板的跳飞角数值模拟结果、修正模型计算结果均与试验结果吻合较好，说明在一定的速度及靶板厚度下本文研究跳飞角的方法是相对可靠的。

表2 结果对比

4 结论

通过本文的数值模拟、理论分析并结合验证试验研究可以发现：①弹体撞击靶板时形成类似Steven B提到的塑性铰链，且铰接点随着侵彻的进行沿着靶板面向前推动。②得到了一系列不同靶板厚度的跳飞角，且随着靶板厚度的增加，着角因素对跳飞的影响呈强化趋势，而靶板厚度因素呈逐渐弱化趋势。③在仿真分析的基础上进行了试验验证，仿真与试验的一致性较好，验证了仿真的可靠性。考虑靶板厚度，对Tate跳飞模型进行了修正，修正模型计算结果与前两者的结果均吻合得较好，该修正模型可以对一定速度下薄装甲钢靶跳飞特性的研究提供借鉴，并对薄装甲结构的设计及优化提供一定的依据。

［1］吴荣波，陈志刚，王庆华.入射角对跳弹现象影响的数值模拟［J］.设计与研究，2011，10（38）：18－32.WU Rong－bo，CHEN Zhi－gang，WANG Qing－hua.Numerical simulation on the impact effect of incidence angle impacting ricochet［J］.Design and Research，2011，10（38）：18－32.（in Chinese）

［2］荣光，薛晓中，孙传杰.异型弹芯斜倾彻靶板的数值分析［J］.弹道学报，2009，21（1）：5－8.RONG Guang，XUE Xiao－zhong，SUN Chuan－jie.Numerical analysis of a non－circular cross－sectional projectile oblique penetrating into target［J］.Journal of Ballistics，2009，21（1）：5－8.（in Chinese）

［3］JONAS G H，ZUKAS J A.Mechanics of penetration：analysis and experiment［J］.Int J Eng Sci，1978，16：879－903.

［4］TATE A.A simple estimate of the minimum target obliquity required for the ricochet of a high speed long rod projectile［J］.J Phys D，1979，12：1 825－1 829.

［5］ROSENBERG Z，YESHURUN Y，MAYSELESS M.On the ricochet of long rod projectiles［C］／／Proceedings of the 11th International Symposium on Ballistics.Brussels，Belgium：IBC，1989：942－957.

［6］STEVEN B S.A model for rod ricochet［J］.International Journal of Impact Engineering，2006，32（9）：1 403－1 439.

［7］TATE A.Long rod penetration models—partⅡ：extensions to the hydrodynamic theory of penetration［J］.Int J Mech Sci，1986，28（9）：599－612.

［8］赵国志.穿甲工程力学［M］.北京：兵器工业出版社，1992：106－107.ZHAO Guo－zhi.Armour－piercing engineering mechanics［M］.Beijing：Ordnace Industry Press，1992：106－107.（in Chinese）［9］DANESHJOU K，SHAHRAVI M.Penetrator strength effect in long－rod critical ricochet angle［J］.International Journal of Impact Engineering，2008，22（11）：2 076－2 089.