时间序列在化工产品温度测量中的应用研究

段美华 殷 莹

（1.天津职业技术师范大学理学院，中国 天津300222；2.天津职业技术师范大学机械工程学院，中国 天津300222）

0 前言

20世纪二、三十年代，美国人休哈特博士首先提出过程控制的概念与实施过程监控的方法，经过几十年的发展，现己形成统计过程控制理论，即SPC(Stat_istical Process Control)。它是应用统计方法对过程中的各个阶段进行监控，从而达到保证与改进质量的目的。统计中我们常假设观察值为来自某总体的独立同分布样本，之后考虑总体某些特征的估计，然而，在实际问题中，观察到的数据多与时间有关且可能是相关的。针对这些相关数据的建模及预测我们采用了时间序列。

1 自相关函数

1）μ1=c,其中c为一常数

2）E（X2t）＜∞,即二阶矩有限

3）γ（t，s）＝γ（t-s，0）

2 P阶自回归序列AR（P）的相关结构

在平稳时间序列分析中，常见的三种模型为自回归AR(p),移动平均MA(q)和自回归移动平均序列ARMA(p,q)模型。这里我们只研究AR(p)模型。

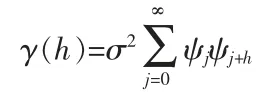
特别地，当P=1,即对于AR(1)序列，ψj=φ-1j，γ（h）＝φ-1h

另外，对于AR(P)序列的自协方差函数，我们还有如下迭代公式：

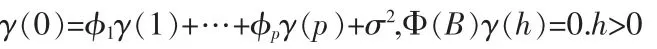
如在上式中取h=1,2,...,p,则有如下的Yule-Walker方程,其中

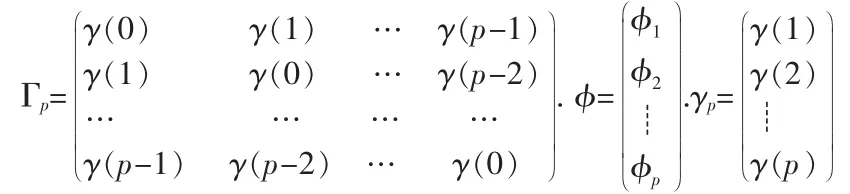
对于AR(p)序列而言，其最主要的特征是其偏相关函数具有截尾的特点。其偏相关的定义为：对于任一给定的k＞0，我们记αk=（αk1，…，αkk），且αk＝Γ-k1γk，则称｛αkk，k=0，1，2，…｝为AR(p)序列的偏相关函数，其中α00=1。

可以证明：零均值的平稳序列｛xi｝为AR(p)序列的充要条件是αkk=0，∀k＞p。由此可见，偏相关函数截尾性质是用来判断一组数据是否来自AR模型的有效方法。

3 实例

某化学工厂需就其某种化工产品的温度进行测量，以便决定其是否合格。表1所示的数据为该工厂对该产品每2分钟进行一次温度测量的结果（从左到右，共100次测量）。

表1 产品温度测量记录表

（1）由于数据的相关性对检测的效果有极大影响，所以对于这些温度测量结果，首先比较重要的是研究这些数据的相关性。因此，我们根据表1，通过minitab计算样本自相关函数和偏自相关函数，其中显著性限制为0.05,结果如图1所示。

图1

自相关函数图a的正弦慢衰减表明了测量数据符合自回归过程，而偏自相关函数图显示自回归过程的阶数为1。

（2）基于上面的分析，对于这些测量数据，我们构造一阶自回归模型xt=ξ+φxt-1+εt，并就该模型建立一个基于残差的单值控制图，如图2。

对图2结果进行分析可知，第94个温度记录值偏离中心线超过了3δ值，即第94个温度记录值为失控；第69、70、71这3个连续温度记录值中，有2温度值（第69个和71个）偏离中心线超过了2δ值。并可以看出，在最初的温度记录中，残差不表现出周期性,且分布在控制限之内，即化学过程可控。

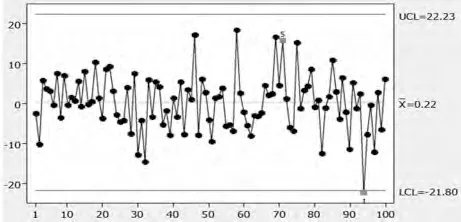
图2 基于残差的单值控制图

（3）就上述模型，我们现在分别构造基于残差的CUSUM和EWMA控制图，如图3。其中CUSUM控制图中k=0.5,h=5；EWMA控制图中λ=0.1,L=2.7。

图3

从CUSUM控制图可以看出，没有观察值超过控制限，残差可控,即过程可控。

这与残差的单值控制图所得到的结论是一致的。从EWMA控制图也可以看出，没有观察值超过控制限，残差可控,过程可控。这与残差的单值控制图和CUSUM控制图所得到的结论一致。

4 结论

从上面对化工产品温度测量数据的分析知，为了避免测量数据有相关性，我们可以通过时间序列中的相关函数图选择更好的模型，以便在以后的检测中减少错误报警率，提高效率。而且该方法也适用于其他方面的测量数据的研究。

［1］安鸿志.时间序列分析[M].华东师范出版社,1992.

［2］王兆军，邹长亮，李忠华.统计质量控制图理论与方法[M].南开大学数学科学学院统计系,2013.

［3］王沁.时间序列分析及其应用[M].西南交通大学出版社,2008.

［4］Lowry,C.A.,Woodall,W.H.,Champ,C.W.and Rigdon,S.E..Multivariate exponentially weighted moving average control chart[J].Technometrics,1992,34:46-53.