基于右互质分解的纱线张力跟踪控制方法及仿真

李伟锋，王 哲

(中原工学院电子信息学院，河南郑州 450007)

纱线拉伸至断裂所能承受的最大抗拉伸力或拉伸断裂负荷，是研究最多的纱线机械性质之一［1－3］。由于纱线的拉伸变形能力很大，并且具有黏弹性体的性质，纱线拉伸过程所产生的形变情况以及纱线成品质量控制也受到充分的关注［4］。拉力对纱线拉伸性质的影响，可用多元件或一般化的黏弹模型来研究［5－7］。本文利用典型的三元素模型进行分析，加入非线性部分，从而得到更接近实际的模型。

1 纱线张力数学模型

三元素模型，也叫做标准固体模型，可较好地模拟高分子材料黏弹性区的受力与变形关系，用以特定型号纱线的模型建立［8－9］。模型构成如图 1所示。

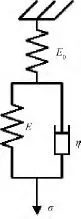
图1 三元素模型Fig.1 Three element model

图中，上部位弹簧的弹性系数为E0，下部位弹簧的弹性系数为E，牛顿型黏滞杯的阻尼系数为η。整个模型受到的应力设定为σ，相应的应变为ξ。于是构建如下方程组:

式中:ξ1、ξ2分别为弹簧 E0和弹簧 E、黏滞杯 η 的应变;σ1、σ2分别为弹簧E和黏滞杯η受到的应力。

将方程组(1)化简，得到下面等式:

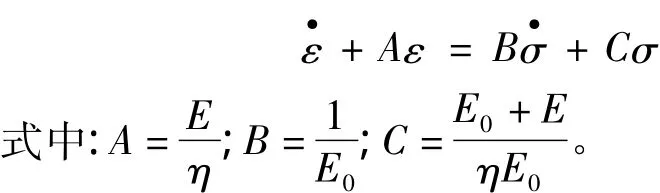
继续化简，得出如下传递函数的形式:

再转化为状态空间方程的形式，即为

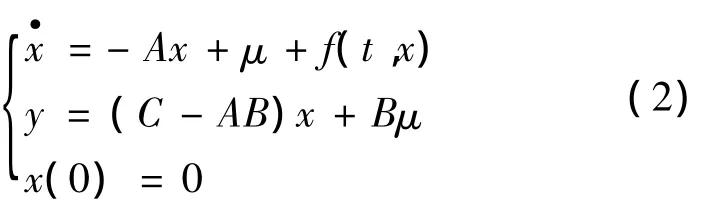
式中:x为状态变量;μ为输入;y为输出;f(t，x)为纱线拉伸过程中的非线性扰动部分。该模型即为单根纱线张力模型的数学表示形式，该状态空间方程即为单根纱线张力数学模型的算子。

2 右互质分解

互质分解的概念最早出现在线性反馈控制系统中，并对反馈控制系统的输入输出稳定问题提供了合理的解决方案。之后，非线性控制系统的互质分解问题开始出现，指导并应用于非线性系统的分析、设计、镇定和控制当中，尤其是非线性系统的右互质分解问题，得到了更为广泛的关注［10］。

定义:如果P存在右分解P=ND－1，且存在因果稳定的映射A∶Y→U，B∶U→U使如下的Bezout恒等式成立:

或

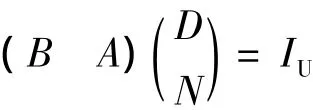
式中IU为U上的单位映射。则称算子P具有右互质分解。

3 纱线张力模型的右互质分解

上文中，计算得到了纱线张力模型的算子，在此，将证明该算子具有右互质分解并计算得到右互质分解的结果。

对于方程组(2)的右互质分解结果，D和N分别写作如下形式:

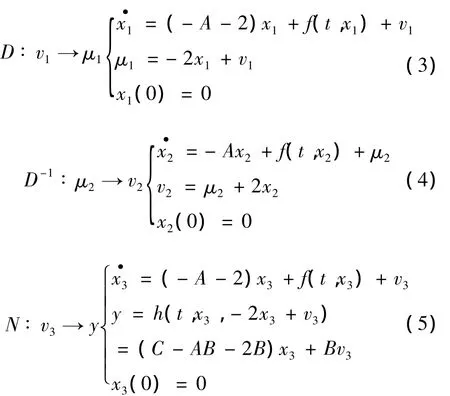
下面根据算子右互质分解的定义来证明P=ND－1且N和D满足Bezout恒等式。

由式(4)、(5)，可得到:

对于任意的输入μ，都有x2(t)≡x3(t)，因此上式与式(1)是相同的，即算子P具有右分解。

式中，v1=v3=v，x1=x3，因此得到(K1N+K2D)(v)=v(v∈U)，即满足 AN+BD=I(A 即 K1，B 即K2)，故算子P具有右互质分解。

4 纱线张力的跟踪控制系统设计

综合以上各部分的分析结果，基于右互质分解的理论，对纱线张力进行跟踪控制的设计研究，设计控制器和反馈状态矩阵，结果如图2所示。

图2 纱线跟踪控制结构框图Fig.2 Yarn tracking control structure diagram

图中:r为期望输入值;b为反馈值;e为误差量;y为输出值;u为纱线系统的输入;P为右互质分解后的纱线模型。

根据图2的结构，计算得到输出y=CN(r)，因此，如果令C=N－1，那么系统就可完成跟踪工作。

5 仿真

使用MatLab/simulink进行模块化仿真，搭建系统模型。为简化计算，假设弹簧E和E0的弹性系数为1，黏滞杯的阻尼系数η为1，则可得到系数A=1，B=1，C=2。则搭建原系统模型如图3所示。仿真结果如图4所示。设定输入期望值为一按正弦变化的序列，分别测试原系统的输出与跟踪控制系统的输出是否能够完全跟踪期望输入。

根据第4节的跟踪控制系统设计，加入控制和反馈部分，仿真系统如图5所示。仿真结果如图6所示。

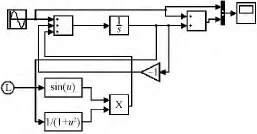
图3 纱线张力系统模型Fig.3 Yarn tension system model

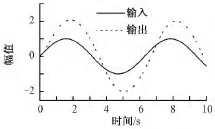
图4 纱线系统模型仿真结果Fig.4 Simulation result of Yarn tension system model

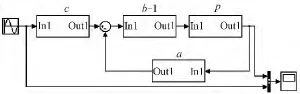
图5 纱线张力跟踪控制系统模型Fig.5 Yarn tension tracking control system model

图6 纱线张力跟踪控制系统模型仿真结果Fig.6 Simulation result of yarn tension tracking control system model

由仿真结果可知，右互质分解之后的纱线张力跟踪控制模型，输出实际值能够完全跟踪输入的期望值，实现纱线张力的跟踪控制。

6 结束语

在纱线的模型基础上，结合右互质分解理论，对纱线张力模型进行分解，并设计得到纱线张力的跟踪控制方法，通过仿真验证了该方法的合理性。该方法能够快速测得纱线张力并对其进行有效的跟踪控制。

［1］ 严灏景.纤维材料学导论［M］.北京:纺织工业出版社，1990:266－295.YAN Haojing.Introduction of Textile Materials［M］.Beijing:Textile Industry Press，1990:266 －295.

［2］ 肖俊明，范福玲，李燕斌，等.纱线拉力试验机测控系统的研制［J］.郑州大学学报:工学版，2010，31(3):38－41.XIAO Junming，FAN Fuling，LI Yanbin，et al.Design of microcomputer monitor and control system for yarn tensile tester［J］.Journal of Zhengzhou University:Engineering Science Edition，2010，31(3):38－41.

［3］ 应腾云，张森林.基于模糊-PI并联控制的经纱张力控制系统［J］.纺织学报，2010，31(9):122－127.YING Tengyun，ZHANG Senlin.Warp tension control system based on fuzzy-PI parallel control［J］.Journal of Textile Reseaarch，2010，31(9):122－127.

［4］ 石风俊.拉伸速度对纱线拉伸试验结果的影响［J］.纺织学报，2003，24(5):537－538.SHI Fengjun.Influence of strain rate on yarn tensile test results［J］.Journal of Textile Research，2003，24(5):537－538.

［5］ 李伟锋，孙启晓，李想.新型土工布胀破性能测试系统的研制［J］.纺织学报，2012，33(7):131－135.LI Weifeng，SUN Qixiao，LI Xiang.Research and development of test system for geotextile expansion rupture performance［J］.Journal of Textile Research，2012，33(7):131－135.

［6］ 张鑫，郭清南，李学磊.压力传感器研究现状及发展趋势［J］.电机电器技术，2004(4):28－30.ZHANG Xin，GUO Qingnan，LI Xuelei.Current status and development tendency of pressure sensors［J］.Technology of Electric Machine and Appliance，2004(4):28－30.

［7］ 丁彩红，唐军.地毯簇绒机纱线牵伸和张力稳定方法［J］.东北大学学报:自然科学版，2009，35(2):206－210.DING Caihong，TANG Jun.Methods of yarn pulling and yarn tension’s stabilization in carpet tufting machine［J］.Journal of Donghua University:Natural Science Edition，2009，35(2):206－216.

［8］ 黄成，吴镇宇.棉纱拉伸性质的建模研究［J］.机电工程，2012，29(2):177－179.HUANG Cheng，WU Zhenyu.Modeling the tensile property of cotton yarn［J］.Journal of Mechanical ＆Electrical Engineering，2012，29(2):177 －179.

［9］ 石风俊，郭会清.拉伸速度对棉纱拉伸性质的影响［J］.纺织学报，2003，24(3):204－205.SHI Fengjun，GUO Huiqing.Influence of strain rate on the tensile properties of the cotton yarn［J］.Journal of Textile Research，2003，24(3):204 －205.

［10］ CHEN Guanrong，HAN Zhengzhi.Robust right coprime factorization and robust stabilization of nonlinear feedback control systems［J］.IEEE Transaction on Automatic Control，1998，10(10):1505 －1510.