基于水均衡方法的隧道涌水量概率预测

王晓明，曹正波

（1.河北省交通规划设计院，河北 石家庄050011；2.河北工业大学土木工程学院，天津300401）

0 引言

涌突水灾害是隧道工程中常见的灾害，准确预测隧道的涌水量对于保证隧道施工、降低隧道施工风险及隧道防排水设计具有重要意义。关于隧道涌水量的预测，许多学者做了大量的研究工作并取得了一定的成果。Coli M和Pinzani A对隧道工程中的水文地质问题进行了综述，将涌水量的计算方法概括为三类：经验法、解析法和数值法[1]。Kong W K 对四种常用的解析方法进行了讨论，并提出了硬岩隧道的涌水量评估步骤[2]。罗敏等采用基于层次分析-模糊综合评判的随机数学方法预测隧道涌水量[3]。王建秀等采用正演和反演方法分别计算了隧道施工前后的涌水量[4]。郭纯青和田西昭采用流量衰减分析法、物理模拟和BP 神经网络模型3者相结合的方法对岩溶隧道涌水量进行综合预测[5]。

在诸多隧道涌水量预测方法中，基于水均衡原理的降水入渗法是一种简便可行的方法，在隧道可行性研究及勘察阶段受到青睐。该方法的计算公式简单，未知参数仅有3个，但是获得准确的参数值较为困难，而确定参数的变化范围是较为容易的。本文采用降水入渗法，结合蒙特卡洛（Monte Carlo）随机模拟技术，对河北省水峪隧道涌水量进行概率研究，进而确定隧道涌水量的置信上限，为隧道防排水设计提供依据。

1 降水入渗法

隧道穿过含水地层时，在隧道影响范围（集水范围）内渗入补给的水量与隧道涌水量应保持平衡状态，因此隧道涌水量可通过式（1）计算。

式中：Q为隧道的正常涌水量（m3/d）；α为降水入渗系数；W为年降水量（mm）；A为隧道通过含水体地段的集水面积（km2）。

《铁路工程水文地质勘察规程》[6]给出了降水入渗系数的经验数据。隧道穿过的地层主要为碎石、微～强风化砂岩和蚀变安山岩，岩体较破碎～较完整，综合确定的降水入渗系数α为0.15～0.30。由于各段岩体的裂隙化程度不尽相同，α可视为随机变量，按均匀分布考虑。该区域的年降水量均值为458.2mm，标准差为120.8mm，可按正态分布考虑。隧道的集水面积与地形有关，在地形图上以隧道边界为起点向两侧地形等高线作垂线，延伸至隧道两侧的分水线，标记出终点；将所有垂线的终点按顺序连接就可以圈闭出一条曲线，曲线所包含的面积即隧道的集水面积。由于集水面积的圈定具有较大的不确定性，将其也视为随机变量，根据多次圈定的结果，集水面积的均值为0.196km2，标准差为0.017km2。

2 蒙特卡洛随机模拟技术

蒙特卡洛随机模拟是根据某一随机变量的概率分布形式及其特征参数（如均值、标准差），利用一定的随机数生成方法，生成概率分布形式与该随机变量的分布形式相同的随机数序列。蒙特卡洛随机模拟的第一步是获得[0，1]区间上的均匀分布随机数（标准均匀分布随机数），再在此基础上进一步获得服从其他分布形式的随机数。在蒙特卡洛随机模拟中，要用到服从不同分布形式的随机数，它们是在标准均匀分布随机数的基础上，通过一定的变换处理得到。随机变量的抽样有许多种不同的方法，最常用、最有效的是直接抽样法（反函数法），另外还有复合抽样法、舍选抽样法、变换抽样法、值序抽样法等[7]。

直接抽样法的原理是：设随机变量t服从分布p（t），累计分布函数为P（t），则P（t）的值域为[0，1]，因此可以把均匀分布随机数ui作为P（ti）的函数值。根据分布与累计分布的关系，则有：

这样就可以在ui与P（ti）之间建立u与t的对应关系，通过式（2）求反函数，可得：

把具体的p（t）代入式（3），通过求反函数可以得到式（2）的具体表达式。计算涌水量的参数服从均匀分布和正态分布，所以本文仅给出均匀分布与正态分布的抽样表达式。[a，b]区间均匀分布的随机变量的抽样公式如式（4）所示：

服从一般正态分布的随机数t的抽样公式如式（5）所示：

式中：μ、σ分别为正态分布函数的均值和标准差；u1、u2为不同的[0，1]区间上的均匀分布随机数。

降水入渗系数、年降水量和隧道集水面积的分布类型及参数已经确定，因此可采用蒙特卡洛法对这三个参数进行随机生成。

3 隧道涌水量概率分析

采用Excel 2003 完成计算，通过rand( )函数产生[0，1]区间上的均匀分布随机数，然后根据各参数的分布类型及特征参数，采用式（4）和式（5） 生成相应的随机数，进一步通过式（1）计算出隧道涌水量。对各参数进行1 000 次随机生成，共计算出1 000 个涌水量值，其分布情况见图1。

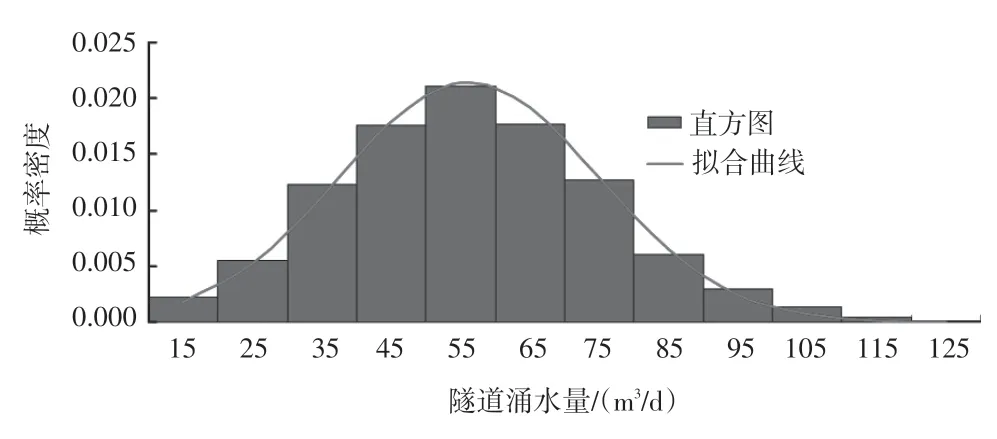
图1 隧道涌水量概率分布及拟合曲线

从图1中可以看出，隧道涌水量的概率分布形式近似为正态分布，采用正态分布曲线对其进行拟合，拟合效果良好。隧道涌水量Q的均值为56.215m3/d，标准差为18.610m3/d。接下来，采用卡方拟合检验法（χ2检验或Chi-test）对隧道涌水量是否服从正态分布进行假设检验。检验统计量χ2的计算见式（6）：

式中：k为根据样本值划分而成的区间数（即直方图中的直方数），对于图1而言，k=12；fi为样本观测值落入第i个区间的个数；n为样本容量；i为pi的估计值，代表检验分布函数在第i个区间的概率，通常根据样本参数进行估计。

隧道涌水量的卡方拟合检验计算见表1。

表1 隧道涌水量的卡方拟合检验计算表

χ2的拒绝域为：

式中：α为显著性水平，一般取0.05；r为检验分布函数中被估计参数的个数，因为均值和标准差均通过样本估计得到，所以r=2。

在计算过程中，对ni＜5 的组进行合并，如对表1中最后三行进行了合并，并组后k=10。经计算，χ2=13.48，χα2(k-r-1)=χ0.052(7)=14.067，χ2＜χα2(k-r-1)。因此，隧道涌水量服从正态分布函数。

基于安全方面考虑，取置信概率为5%对应的涌水量作为预测值，这样能够保证涌水量计算值低于预测值的概率为95%，这样确定的涌水量预测值实质是涌水量单侧置信区间的上限值。经确定，涌水量的预测值为89.340m3/d，该值可作为隧道防排水设计的依据。

4 结论

基于水均衡原理的降水入渗法是一种预测隧道涌水量的简单方法，在隧道可行性研究及勘察阶段应用较广泛。本文结合蒙特卡洛随机模拟技术和降水入渗法对水峪隧道的涌水量进行了概率分析。假定降水入渗系数服从均匀分布，年水量和隧道集水面积均服从正态分布。通过对这3个参数进行1 000 次随机实现，计算出1 000 个涌水量值，隧道涌水量的概率分布近似呈正态分布，均值为56.215 m3/d。取置信概率为5%对应的隧道涌水量作为预测值，该值大小为89.340m3/d，可作为隧道防排水设计的依据。

由于降水入渗法只考虑了3个参数，不能反映地质结构对隧道涌水量的影响，因此适用于隧道施工前的涌水量预测。在隧道施工过程中，应根据获得的地质信息及实际涌水量对预测结果进行校核。

[1] COLI M, PINZANI A. Tunnelling and hydrogeological issues: a short review of the current state of the art[J]. Rock Mechanics and Rock Engineeing,2014(47):839-851.

[2] KONG W K. Water ingress assessment for rock tunnels: a tool for risk planning[J]. Rock Mechanics and Rock Engineeing,2011(44):755-765.

[3] 罗敏，许模，任蕊.一种随机数学方法预测隧道涌突水量研究[J].现代隧道技术，47（5）：38-43.

[4] 王建秀，朱合华，叶为民.隧道涌水量的预测及其工程应用[J].岩石力学与工程学报，23（7）：1150-1153.

[5] 郭纯青，田西昭.岩溶隧道涌水量综合预测—以朱家岩岩溶隧道为例[J].水文地质工程地质，38（3）：1-8.

[6] TB 10049—20040（J339—2004），铁路工程水文地质勘察规范[S].

[7] 贾洪彪，唐辉明，刘佑荣，等.岩体结构面三维网络模拟理论与工程应用[M].北京：科学出版社，2008.