球型支座转动摩擦系数测试研究与分析

2014-12-25安平生

交通运输研究 2014年23期

安平生

（宁夏路桥工程股份有限公司，宁夏银川750004）

0 引言

在公路和铁路领域，球型支座因其承载力大、转动力矩小、无老化等特点成为应用最多的桥梁支座结构之一。其由上支座板、球冠衬板、平面及球面耐磨板、下支座板、锚碇组件等结构组成，图1为其结构示意图。其中，上支座板通过镀硬铬或贴覆平面镜面不锈钢板与平面耐磨板组合成平面摩擦副，球冠衬板球面通过镀硬铬或贴覆球面镜面不锈钢板与球面耐磨板形成球面摩擦副。对球型支座的摩擦系数，无论平面还是球面，一般要求其在高温地区（-25～60℃）不高于0.03，在低温地区（-40～25℃）不高于0.05。对支座的转动性能进行检测对保障施工质量具有极大的重要性。

图1 球型支座结构示意图

大量的试验数据表明，对于采用同样摩擦副材质的球面转动摩擦副和平面滑动摩擦副，平面摩擦副的摩擦系数与理论设计赋值符合的较好，可认为实测平面摩擦副的摩擦系数即为设计赋值摩擦系数。而转动摩擦副的摩擦系数明显大于平面摩擦副的摩擦系数，与设计赋值出现了偏离。一般认为是由于球面半径加工误差、球面轮廓度等制造工艺因素以及组装、试验误差等因素引起，本文将从结构原理方面进行更深入的探讨分析。

1 球型支座转动摩擦的结构理论分析

1.1 球型支座转动摩擦系数的测算方法

根据《桥梁球型支座》（GB/T 17955—2009）对球型支座进行转动性能测试的方法如图2所示。

图2 球型支座转动性能测试示意图

采用两个参数完全相同的支座进行对称对置，推动中间的受力板测定转动瞬间的最大载荷作为转动初始摩擦力F的大小，通过转动力臂L可计算出转动力矩，计算公式如下：

同时该标准给出了支座设计转动力矩的计算公式为：

式中：W为支座设计竖向承载力；μR为支座转动摩擦副摩擦系数；R为转动半径。

由式（1）、式（2）知，转动摩擦系数为：

采用这种方式测量时，由于结构的对称性，在开始转动的瞬间，其对称中心I点位置在水平方向上保持不变。

1.2 球型支座实测转动的结构原理分析

球型支座的结构原理简图如图3所示。

以下座板为固定参照，在支座转动的过程中，球冠衬板球面通过球面摩擦副滑移，滑移总长为：

式中：a为支座转动的角度。

同时球冠衬板所镶嵌的平面耐磨板中心P点也产生运动，其运动包络轨迹为r，其值为P点到转动球心的距离。

式中：B为平面摩擦副与球面摩擦副之间最大间距。

故P点运动路径总长为：

在转动运动过程中，上座板在水平方向的运动，对试验对置双支座结构而言，根据上文对I点的分析，整体位移为0（在实际工况中，其受到所支撑的上部结构的约束，水平滑移的位移量也很小，下文仅对试验工况进行具体分析）。设定上座板初始中心位置为与P点对应的P′点，I点到P′点的距离设为l，P′点绕I点运动，受到I点的约束，与P点并不一致，与其将产生相对滑移摩擦，相对滑移位移为：

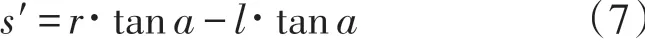
故在支座转动过程中，转动摩擦副和平面摩擦副必然同时产生摩擦，且摩擦的总长为S与s′之和。对一般球支可不考虑压力的分布不均性，在转动过程中，摩擦做功为：

式中：μ为标准摩擦副的摩擦系数，理论上与平面摩擦副摩擦系数μP和转动摩擦副摩擦系数μR相等。

依据能量守恒，有：

由式（1）及式（4）～式（9）得到：

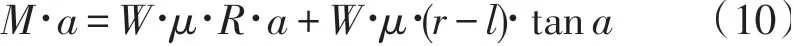
相对于式（2），式（10）不仅考虑了转动面的摩擦，同时考虑了在支座转动过程中，伴随转动摩擦副摩擦发生的平面摩擦副摩擦。一般情况下，球型支座的转角a≤0.05rad，这对于三角函数都很小，tana近似等于a，式（10）可近似转化为：

式（11）为本文分析出的新的转动摩擦系数理论求解公式，这对《桥梁球型支座》（GB/T 17955—2009）中的理论计算式提出了不同的见解，仅仅当r=l时，与式（3）等效，此时点P与P′始终保持重合。

2 有限元分析验证

2.1 有限元分析的设定条件

采用有限元分析能有效避开实际过程中不可完全避免的制造误差及组装试验误差等，在做理论分析时具有相当的优势，借此对本文提出的理论进行验证。在模拟试验加载时，约束下部支座下支座板的所有自由度，约束上部支座下支座板的转动与水平滑动，对对置的两上座板施加转角荷载。有限元网格均采用六面体单元，其中支座钢制部分采用C3D8R单元，耐磨板部分使用C3D8单元，耐磨板的弹性模量为800MPa，泊松比为0.4。对应的有限元网格图如图4 所示，应力云图如图6所示，应力云图显示各个零部件的受力在各自材料的设计承力范围内，相对运动状况都符合预期，各支座的力学与运动状态都满足设计要求。FEA得到的转矩与转角关系如图5所示。

图4 FEA网格图

图5 球型支座转矩与转角关系图

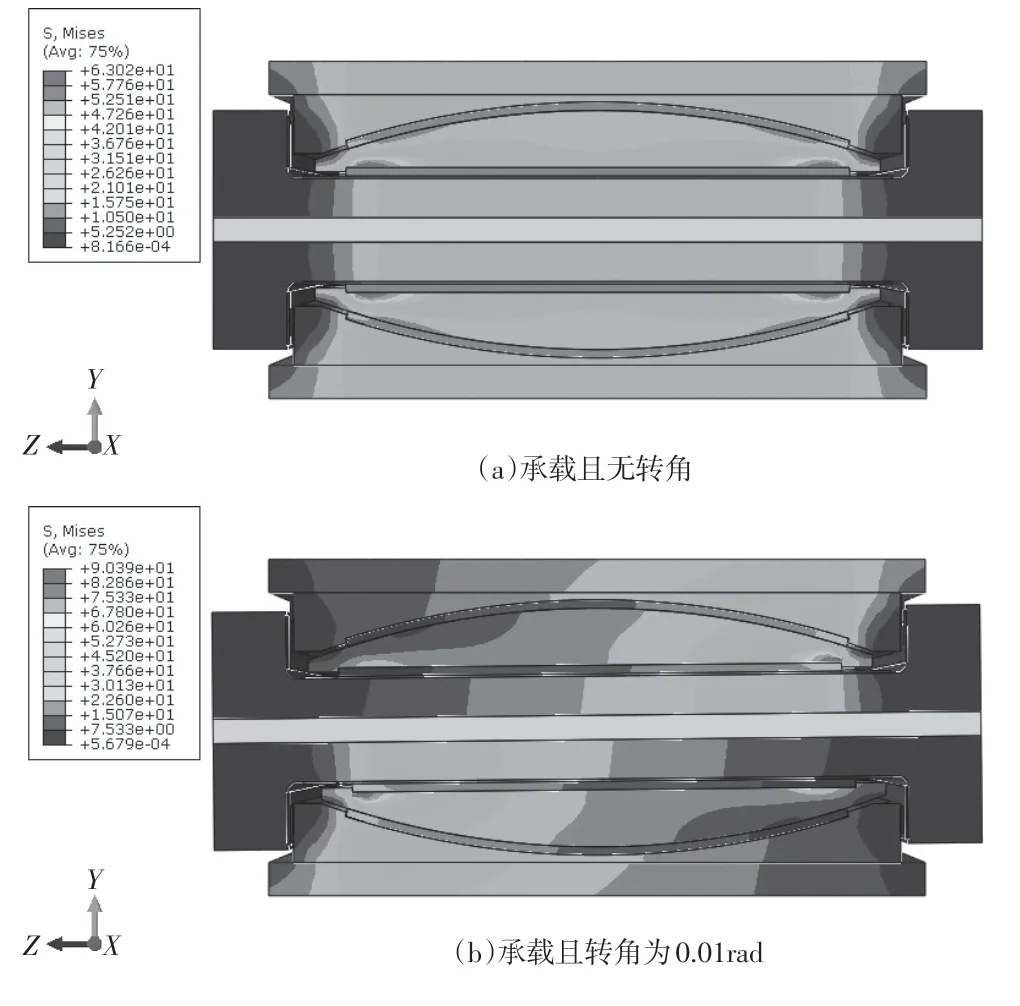
图6 FEA应力云图

2.2 有限元计算结果分析

分析的球型支座相关参数为：竖向承载力W为5MN，转动半径R为675mm，球冠厚度B为50mm，l为45mm，转角a为0.01，设定摩擦系数为0.03。通过对比本文提出的理论公式计算值与FEA测算值，来验证本文结构理论的准确性，数据对比如表1所示。

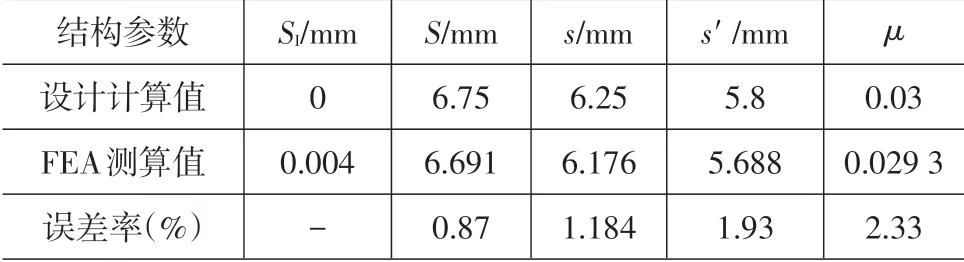
表1 转动理论数据与FEA测算数据对比

对比通过FEA 测算的各个参数与本文理论计算值，即便误差率在各数据中最高的转动摩擦系数，也仅为2.33%，达到了很高的符合度，很好地证明了本文理论推导的准确性。另外，通过对比图6中的FEA云图，可以明显地看到球冠衬板与上座板侧壁的间隙在转动前后由左右间隙相等变为了不相等。

3 摩擦系数实测与对比

通过抽样统计实际检测最常见的竖向承载力为3～10MN 的球型支座（实体测试如图7 所示），对比球型支座实测水平摩擦系数与转动摩擦系数（由式（3）计算得出），发现后者偏移率基本超过前者的100%，如表2 所示。式（11）中的计算因数R+r-l大致为式（3）中相同计算因数的1.85倍，故如果按本文提出的式（11）计算转动摩擦系数，偏移率将缩小为30%左右或更小。