三维自由表面多次波去除方法

王 通，王德利，冯 飞，程 浩，孙海龙

吉林大学地球探测科学与技术学院，长春 130026

0 引言

在海洋地震勘探中，海水表面这个强反射层的存在导致与表面相关多次波［1－2］的发育异常丰富。多次波［3－4］与其他噪音干扰不同，它与一次波有很大的相似性，只是多了一个（或多个）地下的旅行过程，所以用常规的滤波方法［5－6］进行去除往往得不到理想的效果。自由表面多次波预测技术（SRME）［7－8］是一种有效去除与表面相关的多次波的技术。它所采用的数据驱动理念［9］，在不需要任何地下信息的情况下，只利用数据本身就能够预测出与表面相关的多次波。在面对更复杂的地下构造的情况下，笔者提出了三维SRME（3DSRME）处理方法。该方法在增加了横测线方向的多次波能量贡献考虑后，预测出的多次波在波至时间和位置上有了更佳的效果，有效避免了2DSRME处理结果中出现的时间和位置上的错误估计。从处理结果的品质方面来说，3DSRME预测的结果更贴近理论数据中的多次波。

自20世纪50年代起，研究者们提出过许多多次波去除方法。较早的预测反褶积法由Robinson［10］提出；这种方法利用多次波的相关函数从初至的有效波中预测出多次波，然而，由于其局限性，该方法只适用于一维空间介质模型，在海水数据处理中难以得到理想的效果。20世纪末以来，多次波衰减领域有了更迅速的发展。Verschuur等［11］提出了基于CFP技术的层间多次波预测技术法［12－13］，其需要宏观的速度模型作为先验性信息。Herrmann 等［14］、Verschuur 等［15］提 出 了 基 于curvelet变换的多次波压制方法，由于curvelet良好的稀疏特性，多次波的预测减去取得了良好的效果。SRME方法最早出现于1992年，由Verschuur等［15］提出。之后 Dragoset等［16］于1998年验证了2DSRME在模型和实际中的应用效果，发现该方法有时能够取得较好的效果，但大多数情况下的结果都难以令人满意。近些年来，越来越多的三维海洋地震信息的采集及计算机性能的提升，使得3D SRME算法得到了进一步的肯定和发展。1997年，Van Dedem等［17］在SEG会议上发表文章论述了3D算法压制多次波的必要性。2002年，Levin［18］根据近似NMO技术实现了零偏移距的3DSRME，Van Dedem等［19］利用稀疏反演方法进行三维多次波预测。2006年，Baumstein等［20］提出了数据重构方法，将3DSRME技术应用到实际数据中，使得3DSRME技术的发展更贴近实际应用。2010年，Dragoset等［21］指出，在所有多次波预测方法中，三维SRME方法是最能广泛压制表面相关多次波的。

笔者通过论述3DSRME对横测线方向上多次波的贡献，对比水平和倾斜地层下多次波贡献的来源，验证3DSRME对地下介质构造考虑的全面性；建立三维倾斜层状速度模型，模拟含多次波的地震数据，利用3DSRME技术进行多次波预测；利用最小平方匹配减去，实现地震数据中多次波的去除，有效压制了多次波信息。

1 SRME算法原理

数据驱动方法是一种新的处理理念，其完全依靠地震数据本身来进行多次波的预测及压制。依据多次波的传播规律，每个多次波反射都可看成是由若干个一次波或低阶多次波反射构成的，SRME技术实现了将这些反射路径拾取并且有效组合。这种方法在计算过程中仅需地震记录数据、源与检波器之间的参数以及接收到的一次波数据，不需要额外的参数就可完成多次波的预测。所以，只要给出适合的地震数据，在不需要任何地下构造信息的情况下，通过SRME算法就能够预测出表面相关的多次波。

考虑一种宽频的、由水平地面激发的地震波在水平反射界面传播的情形。假设表层界面具反射作用（类似于海洋情形），反射系数为r0，定义地下介质的一次反射响应为R（ω），平面子波为S（ω），这时就能够得到一次波的表达式：

则多次波可以写成

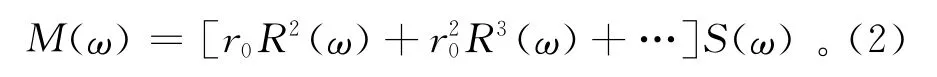
包含多次波的地震数据可以表示成

则对等式（2）提取R（ω）可以写成

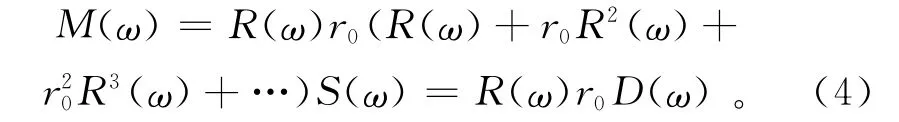
如果所有源的地下岩层响应都能够被再一次记录，就可以获得在3D情况下的自由表面反射多次波：

式中：R（xk，yk，ω；xr，yr）表示在转换点（xk，yk）激发、接收点（xr，yr）接收的地震数据；D（xs，ys，ω；xk，yk）表示在炮点（xs，ys）激发、（xk，yk）点接收的地震数据。这个过程与惠更斯原理非常相近，可以把反射表面解释为一系列将向上传播的波场反射回地下岩层中的二次震源，如此反复，一次波推导出一阶多次波，一阶多次波又推导出二阶多次波，这样一直进行下去。对于式（5）的一种最好的理解是：当给定震源和检波器的地震数据时就能够计算出多次波数据。它描述了源和检波器组合法预测多次波的过程（追踪多次波数据）。

在时间域，式（5）可以写成

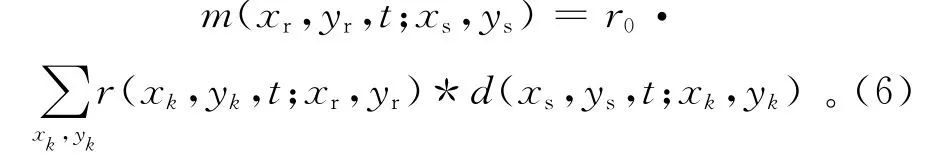
式中：＊表示时间域的褶积；d（xs，ys，t；xk，yk）代表一个共炮点道集；r（xk，yk，t；xr，yr）代表一个共接收点地震子波道集。式（6）将x，y方向都做褶积累加，目的是考虑整个测区地下介质对多次波的贡献，这个算法充分考虑了地下介质的三维特性。将共炮点数据和共检波点数据褶积后，旅行时的物理可实现路径遵循费马时间最短原理，即所有经表面反射的多次波路径都被建立，并通过累加自动筛选对应的物理贡献，获得有效的多次波物理传播路径，削弱其他路径的贡献。

由于SRME是数据驱动的，能够在不考虑多次波在地下介质表面详细传播过程的情况下预测自由表面多次波。因此，那些经过共中心点道集、波形转换、绕射、内反射以及折射产生的多次波都能够被预测到。此外，SRME对波场的传播角度和复杂程度上都没有限制性要求。

2 3DSRME算法

2.1 三维观测系统下的SRME

在地震勘探中，震源激发的地震波呈球面扩散的形式向下传播。地下反射界面并非绝对平面，而是一个粗糙的界面。根据惠更斯原理，当地震波到达这个表面时，产生的反射波并不只沿一个路径传播，而是沿多个路径传播。这样，在表面观测到的地震数据受整个地下介质作用，不局限于单条测线的投影范围内。

图1将地震数据采集过程中的多次波传播进行了简单模拟。假设在S点放炮、R点记录的多次波来自5条测线的贡献。当界面沿y方向上倾时，地下介质对多次波的主贡献会从S-A-O-BR偏移到S-A′-O′-B′-R这条路径上，而常规2DSRME仅利用S-A-O-B-R测线上的数据进行预测，无法估测到实线部分的数据，这样的预测无法贴合实际。3DSRME方法利用所有测线数据，对所有路径都能够重构预测出来，进而从中准确地识别出主能量，达到准确估计的目的。所以想要准确地推断出整个测区对多次波的贡献，有必要进行三维SRME数据处理，或是说3DSRME相对于2DSRME更加切合实际。

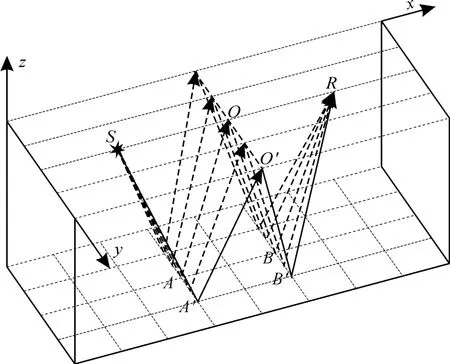
图1 地震波传播路线Fig.1 Propagation path of seismic waves

2.2 横测线多次波贡献

地下各点接收到的多次波能量是地下介质的共同响应。地下各点与接收点之间的距离影响其对多次波贡献的大小。常规情况下，当地下界面为水平层时，多次波的能量主要来自于该测线地下投影的位置（图2a0测线处），此时无需考虑三维处理。但是，当地下界面倾斜时，多次波能量就不再集中于测线的地下投影处，它将沿倾斜方向偏移（图2b）。这种偏移将导致在原测线位置预测出来的多次波不是多次波贡献最大的部分，所得的数据也就不能对多次波产生理想的压制作用。

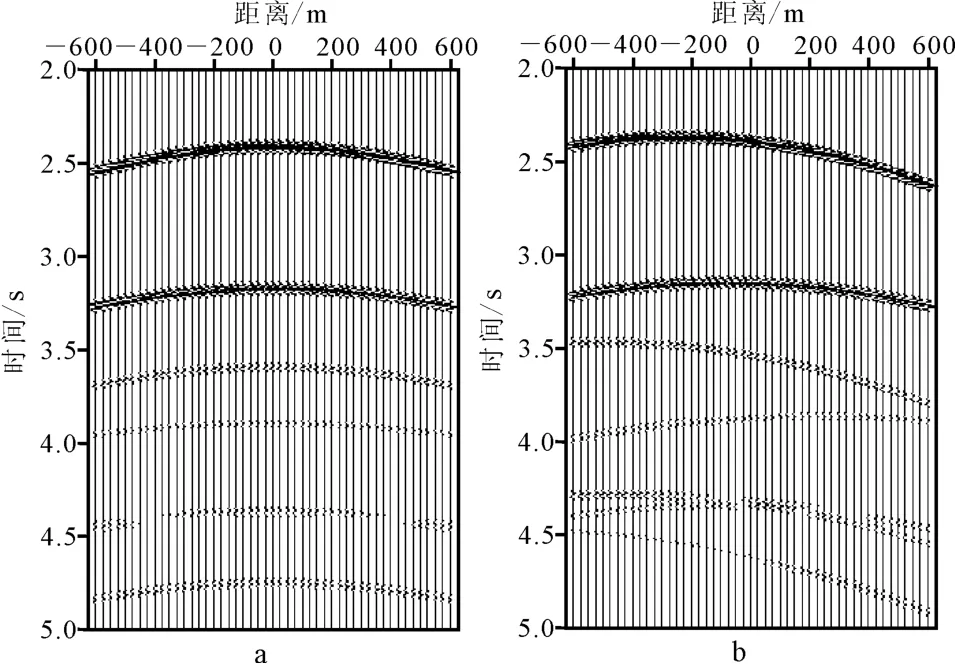
图2 横测线多次波贡献对比Fig.2 Comparison of cross－line multiple contribution

对倾斜反射界面第1 000道数据进行2D、3D SRME多次波预测对比，结果如图3所示。从时间先后上可以明显地看出，对于这种倾斜界面的多次波数据，2DSRME预测的多次波出现的位置存在明显误差。这种错误的预测不但不能消除多次波，有时反而会带来负面影响，引入噪音或削弱一次波能量。而3DSRME预测的多次波在时间上和波形上都很准确，这时只需将预测的多次波数据与原始数据进行匹配减去就能达到压制多次波的目的。

2.3 最小平方匹配减去

由于多次波的预测过程中涉及道集的褶积与累加，这就导致预测出来的多次波在相位和振幅上存在差异，所以要通过匹配减去实现多次波的压制。最小平方匹配滤波是一种自适应的滤波方法，根据最小平方原理，实际处理可分为两步：

1）子波匹配。相当于一个全局滤波器，为每一炮记录求取一个全局逆子波，使原始地震记录与预测出的多次波相减后能量损失最小。预测的多次波和全局逆子波反褶积后，与原始数据就比较接近了。

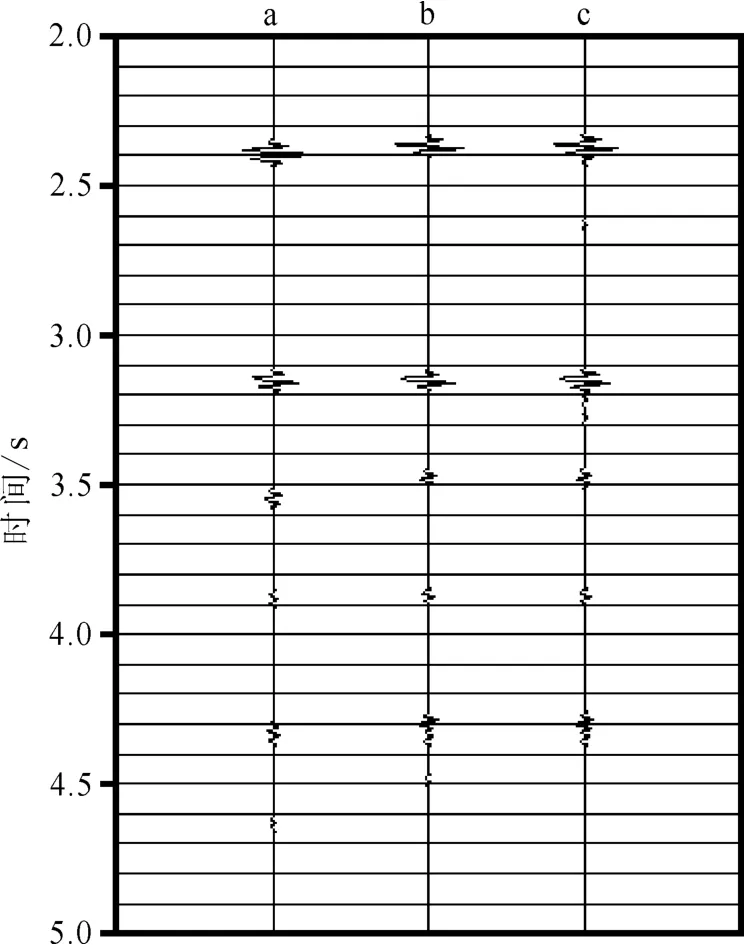
图3 2D、3DSRME方法预测多次波对比Fig.3 Comparison of predicted multiples by 2Dand 3D SRME

2）振幅匹配。相当于一个局部滤波器，通过开取小的时间－空间窗口，在每个窗口内估算一个滤波算子，然后将该滤波算子作用于预测的多次波，得到窗口内匹配的多次波。开取窗口过程中，各窗口间无论在时间上还是空间上都有重叠。经过局部匹配后，把所有窗口内的多次波数据进行整合，对数据边缘进行斜坡处理，得到一个完整的多次波数据。

减去的过程利用最小平方原理使得地震数据中减去多次波数据后一次波能量损失最小，且最大程度地压制多次波。

3 模型试算

3.1 多次波预测

本文利用一个简单的地震反射记录验证3D SRME在预测多次波方面较2DSRME的准确性。

速度模型包含3个反射层，每个反射界面都是倾斜的，模型参数如图4所示。利用射线追踪方法对该速度模型进行正演模拟。正演过程中对整个测区进行网格化，网格间距为10m×10m；每个节点都进行放炮接收，得到全测区的三维地震观测数据。

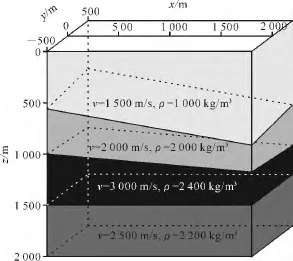
图4 正演中所用的速度模型Fig.4 Velocity model used in the forward modeling

抽取0测线1 000m处（1 000，0，0）放炮数据作为要预测的目标数据，截取多次波发育的部分，在地震剖面（图5a）上主要出现在1.7s后。首先，利用0测线数据自身褶积实现2DSRME多次波预测，如图5b所示。然后，对全测区数据进行整理形成一个三维数据矩阵，三维矩阵自身褶积实现3D SRME多次波预测，抽取0测线1 000m处炮点数据如图5c所示。对比图5a、b、c可以看出，3D SRME预测的多次波（图5c）从直观上就与原始地震记录（图5a非常吻合）。图5c中多次波的波至时间预测准确，没有出现图5b中多次波波至时间整体延后的现象。这是由于三维的多次波预测准确拾取了多次波贡献道集上能量聚集点，未受单条测线内假能量顶点的干扰，确保了预测的准确性。再看能量轴间的交叉关系，图5a与图5c完全相同，未出现图5b中错误的交叉点，基本达到准确的多次波预测。

为更加明了地显示预测结果上的差异，将图5中差别明显的局部（箭头处）进行截取、放大，呈现在图6中。通过局部对比更加明显地看出2DSRME方法在地层倾斜的情况下预测多次波存在的问题，相比于此，3DSRME算法可以给出更加准确的波至时间和相位振幅。对比图6a1、a3可以发现，在测线的边缘处，3DSRME方法同样会出现多次波振幅不足的情况，这是由于数据边缘化引起的，对整体方法的可靠性不构成影响。

3.2 多次波匹配减去

对上面预测的多次波数据采取最小平方匹配减去法进行多次波去除，减去效果如图7所示。图7中上方的3条同相轴代表地下的3个反射界面，下方代表多次波的去除结果。从图7中可以看出，2D SRME匹配减去结果（图7a）下方残留着较多的多次波信息，而3DSRME匹配减去结果（图7b）多次波基本被去除干净。截取图7a、b相同位置进行放大，提高幅度对比（图8）。从图8中可以发现，在2DSRME匹配减去结果中多次波残留较为严重的箭头处，并未在3DSRME匹配减去结果相同位置出现残留。究其原因，由于最小平方匹配减去的第二步是在小的时空窗口匹配的，而2DSRME预测的多次波在时间－空间位置上出现错动，无法实现窗口内的匹配，所以在匹配减去中无法有效地压制原始数据中的多次波，甚至带来干扰信息或损伤一次波。反观3DSRME预测结果的匹配相减，准确的多次波预测使得匹配减去过程中原数据中多次波部分基本消除干净。这也说明在准确的预测下匹配相减才能带来更好的结果。

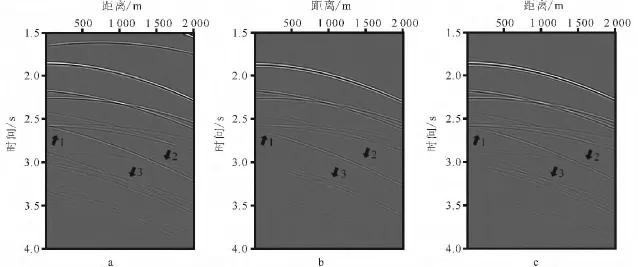
图5 多次波预测结果对比Fig.5 Comparison of multiple predictingresults

图6 多次波预测局部对比Fig.6 Local comparison of multiple predicting

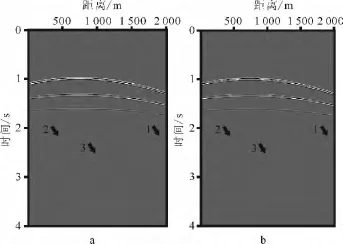
图7 多次波预测匹配减去结果对比Fig.7 Comparison of results by multiple subtraction method

4 结论与展望

1）从地震波的波场传播方式来看，2DSRME算法从根本上就把地下介质考虑成了二维介质，这与实际情况不相符，不适合于3D海洋地震数据的多次波预测。

2）3 DSRME方法是数据驱动的，在进行模型正演数据试算过程中，没有涉及到地下介质的任何信息，只利用地震数据本身即可有效地预测出多次波。

3）3 DSRME方法在考虑多次波的贡献方面是很完善的，该方法可以对接收测区内所有可能的多次波路径进行计算，并给出其相应的贡献值。

图8 匹配减去结果局部对比Fig.8 Local comparison of results by multiple subtraction method

4）通过对复杂模型的模拟数据的处理发现，3D SRME技术能够准确预测多次波信息，对多次波的压制工作提供坚实的理论基础。然而笔者在模型正演地震数据过程中，对于地震数据的采集是浓密的，这种对数据过高的要求在实际生产中难以满足，在稀疏情况下3DSRME方法的应用还有待于提高和完善。目前已有一些较好的应对稀疏数据的方法，如实时插值法和稀疏反演方法预测多次波。

（References）：

［1］沈操.基于波动方程的自由表面多次波压制［D］.北京：中国地质大学，2002.Shen Cao.The Suppression of Free Surface Multiples Based on the Wave Equation［D］.Beijing：China University of Geosciences，2002.

［2］冯飞，王德利，张亚红，等.结合曲波变换的焦点变换在地震数据去噪和插值中的应用［J］.物探与化探，2013，37（3）：480－487.Feng Fei，Wang Deli，Zhang Yahong，et al.The Application of Focal Transform in Combination with Curvelet Transform to Seismic Data Denoising and Interpolation［J］.Geophysical and Geochemical Exploration，2013，37（3）：480－487.

［3］刘建辉.基于波动理论压制多次波方法研究［D］.北京：中国石油大学，2010.Liu Jianhui.Research of Multiple Suppression Method Based on Wave Theory［D］.Beijing：China University of Petroleum，2010.

［4］王德利，党丹，刘伟明，等.CFP技术层间多次波预测及Curvelet域相减方法［J］.吉林大学学报：地球科学版，2011，41（3）：908－914.Wang Deli，Dang Dan，Liu Weiming，et al.Internal Multiples Prediction Based on CFP Approach and Curvelet Domain Subtraction［J］.Journal of Jilin University：Earth Science Edition，2011，41（3）：908－914.

［5］胡天跃.地震资料叠前去噪技术的现状与未来［J］.地球物理学进展，2002，17（2）：218－223.Hu Tianyue.The Current Situation and Future of Seismic Data Prestack Noise Attenuation［J］.Progress in Geophysics，2002，17（2）：218－223.

［6］张旭东.几种多次波压制方法讨论［J］.内蒙古石油化工，2011（1）：84－85.Zhang Xudong.Discuss on Several Multiple Wave Suppression Method［J］.Inner Mongulia Petrochemical Industry，2011（1）：84－85.

［7］李东升，帕提幔.利用波动方程预测减去法压制海洋地震资料中的多次波［J］.石油地球物理勘探，2007，42（8）：57－60.Li Dongsheng，Pa Timan.Using the Method of Wave Equation to Predict Minus Suppress Multiples in Marine Seismic Data［J］.Oil Geophysical Prospecting，2007，42（8）：57－60.

［8］Feng Fei，Wang Deli，Zhu Heng，et al.Estimating Primaries by Sparse Inversion of the 3DCurvelet Transform and the L1－Norm Constraint［J］.Applied Geophysics，2013，10（2）：201－209.

［9］Dragoset B，Verschuur D J，Moore I，et al.A Perspective on 3DSurface－Related Multiple Elimination［J］.Geophysics，2010，75（5）：245－261.

［10］Robinson E A.Predictive Decomposition of Seismic Trace［J］.Geophysics，1957，22：767－779.

［11］Verschuur D J，Berkhout A J.Removal of Internal Multiples with the Common－Focus－Point（CFP）Approach［J］.Geophysics，2005，70（3）：61－72.

［12］党丹.CFP层算法及Curvelet变换层间多次波压制方法研究［D］.长春：吉林大学，2012.Dang Dan.The Study on Removing Internal Multiples with CFP Layer［D］.Changchun：Jilin University，2012.

［13］刘伟明，王德利，张亚红.CFP方法衰减层间多次波研究［C］//中国地球物理·2009.北京：中国地球物理学会，2009.Liu Weiming，Wang Deli，Zhang Yahong.The Study on Removal of Internal Multiples with the Common－Focus－Point（CFP）Approach［C］//The Chinese Geophysics·2009.Beijing：Chinese Geophysical Society，2009.

［14］Herrmann F J，Wang Deli，Hennenfent G，et al.Multiple Prediction from Incomplete Data with the Focused Curvelet Transform［C］//Society of Exploration Geophysicists 77th Annual International Meeting.San Antonlo：Society of Exploration Geophysicists，2007.

［15］Verschuur D J，Wang Deli，Herrmann F J.Multiterm Multiple Prediction Using Separated Reflections and Diffractions Combined with Curvelet－Based Subtraction［C］//Society of Exploration Geophysicists 77th Annual International Meeting.San Antonlo：Society of Exploration Geophysicists，2007.

［］， ˇ＇

16 Dragoset W HJericevicŽeljko.Some Remarks on Surface Multiple Attenuation［J］.Geophysics，1998，63（2）：772－789

［17］Van Dedem E J，Verschuur D J.Analysis of Surface－Related Multiples in 3－D Media［C］//Society of Exploration Geophysicists 67th Annual International Meeting.［S.l.］： Society of Exploration Geophysicists，1997：1180－1183.

［18］Levin S A.Prestackpoststack 3DMultiple Prediction［C］//Society of Exploration Geophysicists 72th Annual International Meeting.［S.l.］：Society of Exploration Geophysicists，2002：2110－2113.

［19］Van Dedem E J，Verschuur D J.3DSurface－Related Multiple Prediction Using Sparse Inversion：Experience with Field Data［C］//Society of Exploration Geophysicists 72th Annual International Meeting.［S.l.］： Society of Exploration Geophysicists，2002：2094－2097.

［20］Baumstein A，Hadidi M T.3DSurface－Related Multiple Elimination：Data Reconstruction and Application to Field Data［J］.Geophysics，2006，71（3）：25－33.

［21］Dragoset B，Verschuur E，Moore L，et al.A Perspective on 3DSurface－Related Multiple Elimination［J］.Geophysics，2010，75（5）：245－261.