船舶横甩的运动状态研究
2014-12-25张盛龙
张盛龙
(1.上海海事大学,上海201306;2.渤海船舶职业学院,辽宁葫芦岛125105)
0 引言
船舶横甩是随浪航行中的船舶由于某种原因突然失去保持既定航向的能力而发生急速的转向,由于人为无法控制而产生大角度的横倾,使船舶处于极度危险的境况,有统计表明65%的船舶倾覆事故大多数与船舶的随浪现象有关系,且随浪中骑浪运动的发生是从周期运动到骑浪运动的转变,而且骑浪运动是横甩发生的前兆,因此船舶的横甩现象研究显得更加迫切。但是在国内横甩研究并不深入,而且没有一个统一的规范准则可以用来预报和估算船舶的横甩,由于横甩是高度的非线性,船舶试验比理论推导更加适合,闫美松、丁勇根据自航模试验结果,分析了船舶发生横甩的根本原因是由于作用在船体上的波浪艏摇力矩大于舵的稳性力矩,提出船舶横甩除了与有关系,还与波陡、船所处的波面位置和船体型线形状有关。但是没有具体对波浪力进行分析计算;Seizo Motora认为当船长约为波长的二分之一、船速约等于波速时,船舶易发生横甩;范佘明通过建立六自由度操纵运动方程,进行船舶在波浪中的回转运动和Z型操纵运动舵试验,认为在波长约为2倍船长,波速接近航速时,船舶比较容易发生横甩;唐友刚利用自动驾驶仪操纵的自航船模,通过对四个自由度耦合,应用非线性动力学系统研究固定点及局部稳定性,提出船舶在低速时呈现一种周期运动,随着船速的增加出现了航向不稳定性和倾覆现象。本文在总结了前人经验的基础上,将对某渔政船在不规则波浪中的运动模拟进行分析,通过maxsurf中的strip薄片理论对船舶摇荡运动响应进行科学的预报,来估算出船舶发生横甩的范围。
1 建立数学模型
切片理论(strip theory),也叫做薄片理论,起初由Korvin-Kroukovsky提出,之后由Salvensen、Tuck、Faltinsen做了完善。该理论适合于细长体的船舶,因为船舶细长的特点,当有规则或者不规则的波浪经过船舶时,引起了船舶的运动,船体附近的水流中起主要作用的是在船舶轴线与垂直于水平面的流动,但是沿轴向的水流由于船体表面纵向曲率小,影响变得很小,可以忽略不计,这样便可以将三元复杂的流动问题转化为二元流动。这样作用在船体上的流体运动可以由沿船长将这些剖面上的力叠加得到二元剖面的流体动力系数,附加质量及阻尼系数用不同的方法计算。
对于具有较为稳定航速的细长体船舶,经常使用三维纽曼—开尔文方程(N-K方程)加以描述。而所谓切片理论,只是一种被广泛应用的求解该方程的近似方法。切片理论示意图如图1所示,其主要的假设认为波浪辐射与衍射沿船长方向的变化极其缓慢,而这一观点使得对N-K方程可以进行合理的简化。
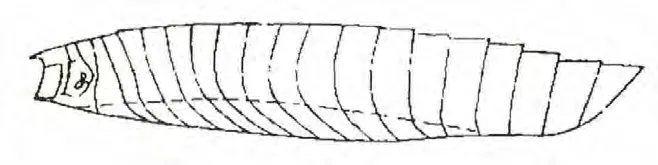
图1 切片理论示意图
将船体各“切片”的流体分为静水回复力、辐射力、绕射力、F-K力,取两个坐标系,一是空间固定坐标O-XYZ,原点在水平面上,OX轴正向与入射波的船舶方向相反。二是随船坐标系o-xyz,原点o在静水中的船舶水线面上且初始时与重心G位于同一铅垂线上,ox轴正方向与航向一致。则入射波的波面方程和遭遇频率如下:
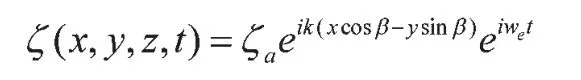
ω——波频;
k——深水波数;
U——船舶航速;
β——浪向角。
将船体周围流场的速度势Ф(x,y,z,t)分解为定常流动和非定常流动两部分:
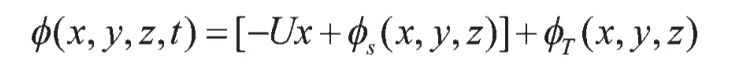
根据伯努利方程,船体表面一点的脉动压力p(x,y,z,t)为:
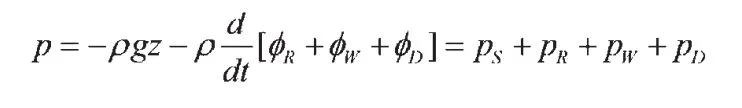
2 计算实例

图2 某渔政船模型

图3 船体剖面划分
本文根据某渔政船为例,利用maxsurf进行建模,其模型如图2所示。船舶基本参数为船长49 m,设计水线长46 m,型宽7.6 m,型深3.9 m,设计吃水2.7 m,设计排水量461.26 t,方形系数0.483。把模型导入seakeeper中进行了在波浪参数为北大西洋波浪谱的模拟计算,那么在规定了波浪的条件之后,傅汝德数Fn便是该系统唯一确定的控制参数。采用strip切片理论计算,船体共划分20个剖面如图3所示,纵摇惯性半径为总长的25%,横摇惯性半径为船宽的35%。利用Gerritsma and Beukelman I算法,因为该算法适合于快速船舶,估算该船散发出的能量为基础。所以用这个方法算某渔政船是可行的。浪的方向定义为任意方向,进行91次迭代计算后,对傅汝德数分别为Fn=0.2;Fn=0.53;Fn=0.8三个不同航速计算进行比较,计算结果如图4所示。
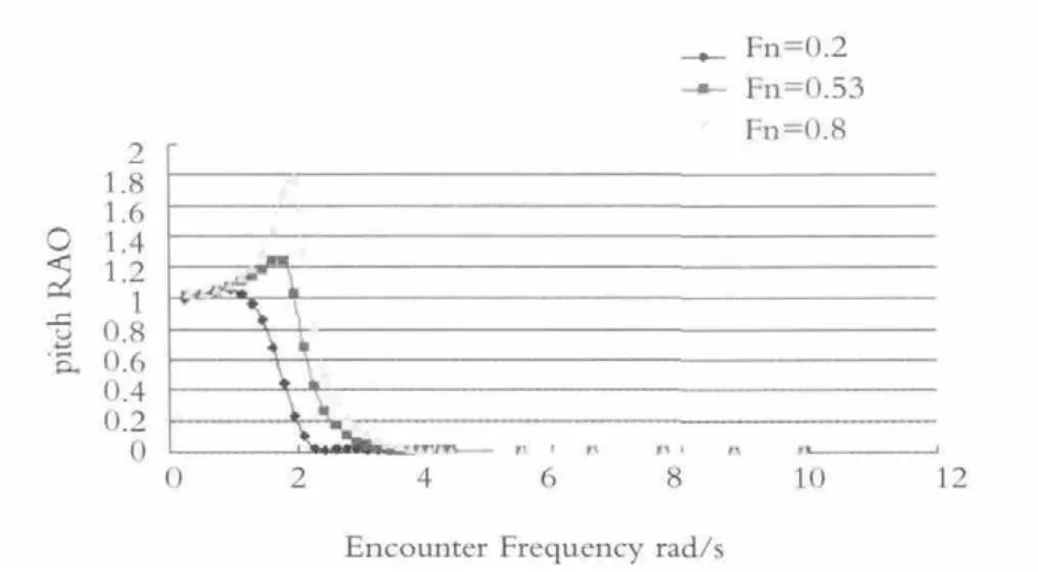
图4 纵摇RAO随遭遇频率的变化曲线
由图4可知,随着傅汝德数的增加,船舶的纵摇幅值响应算子RAO也依次增加,表明当船速越大时,船舶越不稳定,也越容易发生横甩现象。
当0<ω<2时,该船的纵摇幅值响应算子RAO随船舶遭遇频率的变大而变大,但是当ω>2时,纵摇幅值响应算子RAO随船舶遭遇频率的变大而变小,峰值点在频率ω=0.2 rad/s附近,该数据表明当遭遇频率在很小的时候纵摇幅值响应算子RAO很大,在接近于2的时候达到极限。
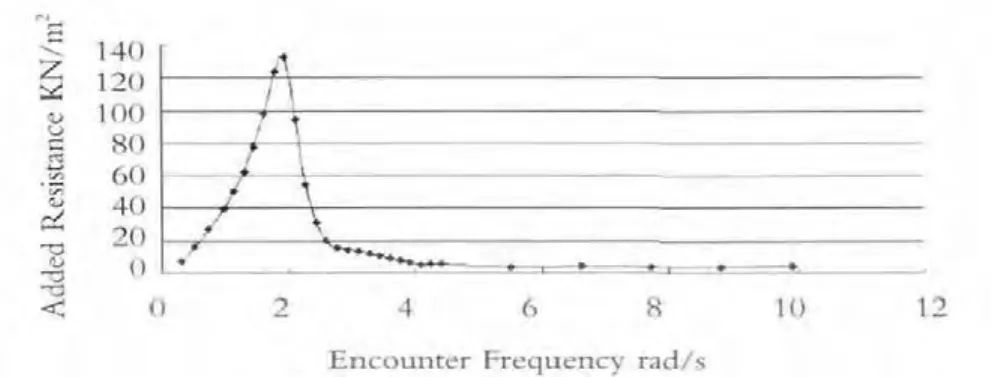
图5 附加阻力随遭遇频率的变化曲线
图5为附加阻力随船舶遭遇频率的变化情况,该阻力不包括由风引起的速度损失。从图中曲线可以看出,在遭遇频率接近2的时候,附近阻力也达到最大值,此时波浪的纵向阻力大于舵的推力,此时首部的力矩不平衡,可以判定船舶容易发生横甩。
3 结语
本文以某渔政船为例,利用seakeeper软件中的Gerritsma and Beukelman I算法对其进行计算,得出该船在遭遇频率峰值点在频率ω=0.2 rad/s附近,纵摇RAO和附加阻力达到极限值,容易发生横甩。
船舶航速越高,发生横甩的几率越大,因此为确保安全航行,尽量减小航速。
[1]陶醉,张纬康.随浪中骑浪现象数值研究[J].武汉理工大学学报(交通科学与工程版),2001(4):447-450.
[2]陶醉,张纬康.操纵性方程在船舶横甩研究中的应用[J].船舶工程,2002(3):23-27.
[3]闵美松,丁勇,赵晓东.随浪中船舶横甩试验研究[J].哈尔滨船舶工程学院学报,1993(3):12-18.
[4]范佘明.船舶在随浪中的运动与横甩预报[J].船舶,2001(1):38-42.
[5]陶醉,张纬康.船舶骑浪运动的分叉研究[J].船舶力学,2004(2):29-33.
[6]陶醉,张纬康.船舶横甩及随浪操纵对策研究综述[J].海军工程大学学报,2001(1):28-34.
