安徽省市域经济增长质量动态模糊综合评价＊——基于改进的AHP－FCE 集成模型

李荣富，傅懿兵，王 萍

（1.池州学院 经济贸易系，安徽 池州247100；2.烟台职业学院 会计系，山东 烟台264000；3.东北财经大学 经济学院，辽宁 大连116025）

在经济体制改革进入“完善社会主义市场经济体制阶段”［4］（2002年至现在），安徽省作为国家实施中部崛起战略的重要区域以及与长三角无缝对接的纵深腹地，实施了一系列的规划与战略，积极推进经济发展，其所辖各地级市亦因地制宜地采取了差异化的区域发展政策。促进经济发展的战略、政策的绩效不仅体现在速度的快慢、数量的扩张方面，更体现在经济增长质量的差异方面。如何判断和分析这一历史阶段安徽各市域经济增长的优劣，以真实有效地总结经济发展的成果，适时地理性反思经济建设实践，纠正不合理的政绩考核观和单纯追逐GDP数量增长的评价机制，有着重要的现实意义，这也正是本文研究的切入点。

本文在经济增长质量内涵基础上，根据安徽省2002—2011年间各市域经济增长的现实情况，综合课题组研究分析和专家咨询结果，构建了多维评价指标体系，运用模糊统计方法采用改进的AHP－FCE集成模型和权威数据进行实证研究，以客观有效地评价分析各市域经济增长质量。

一、经济增长质量评价指标的构建

经济增长质量内涵丰富而且影响因素复杂，需要克服单一指标信息不足的缺限，采用多维度的度量指标。本文遵循科学性、系统性和可操作性的指标设置原则，借鉴学者的前期研究成果［5－8］，从反映经济增长质量的5个维度：经济增长的稳定性、协调性、持续性、潜力和福利性等方面遴选和建立了三层评价指标体系（结果见表1）。其中，一层（或顶层）的经济增长质量是综合评价系统的终级评价目标；稳定性、协调性、持续性、潜力和福利性是系统的二层评价项，以此多维度反映区域经济增长过程中质量的差异；三层为指标体系中的具体20个指标，用以解释对应的二层综合评价项。

二、综合评价集成模型

构建的评价指标（无论是定性的还是定量的指标）只能近似地反映经济增长质量状况，这使得综合评价具有一定的模糊性，同时各评价指标的权重又是影响综合评价的关键因素，因此，如何通过评价指标刻画模糊关系并客观地确定各评价指标权重是解决综合评价问题的根本。根据这一思路，本研究采用 AHP－FCE综合评价模型［9］，即将模糊综合评价法（Fuzzy Comprehnsive Evaluation，FCE）和改进的层次分析法（Adjusted Analytic Hierarchy Process，AHP）进行集成，其基本思想是：模糊关系由各评价指标的相对隶属度表达得到模糊关系矩阵；指标权重是根据AHP原理构造出与模糊关系矩阵具有满意一致性的、改进的AHP判断矩阵通过寻优运算产生的；将模糊关系与权重合成得到模糊综合评价值。下面列出具体的建模步骤［10］。

（一）建立模糊关系矩阵

设各评价指标 的论域U＝｛x1，x2，…，xj，…，xm｝为评价对象或区域所组成的方案集，其中xj表示j市即第j个方案，j＝1，2，…，m。每个方案用i个指标（i＝1，2，…，n）进行评价，则xj＝ ｛xij｜i＝1，2，…n，j＝1，2，…，m｝ 组成对m个方案的评价指标集。则原始数据矩阵表示为：其中xij表示第j个方案的第i个评价指标数据。

根据各评价指标特性（正向型指标、逆向型指标和中间型指标）和数据矩阵X分别计算出单个评价指标对每个方案的相对隶属度rij，i＝1，2，…，n，j＝1，2，…，m 。具体计算方法可以参考文献［9］和［10］。

由各评价指标相对隶属度形成模糊关系矩阵即模糊综合评价矩阵R＝ （rij）nxm，即

EGFR-TKI联合化疗对比EGFR-TKI单药一线治疗EGFR敏感突变晚期非小细胞肺癌患者疗效的Meta分析(柳菁菁)(4):362

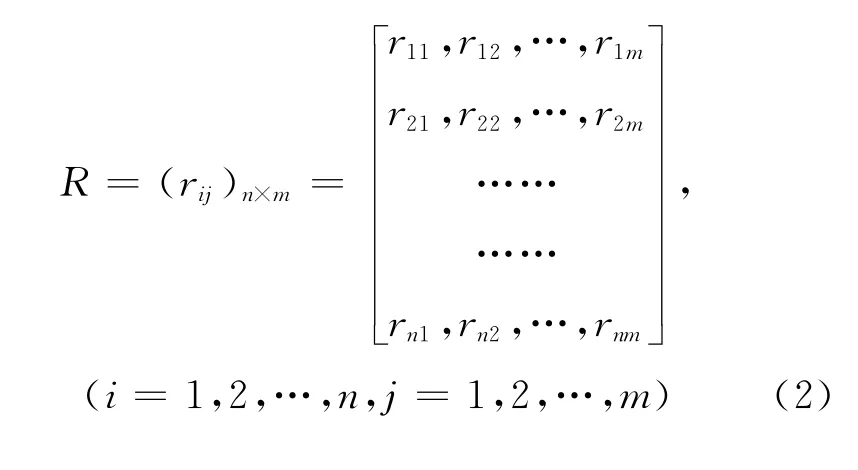
（二）构造AHP判断矩阵

由模糊评综合价矩阵R和层次分析法（AHP）原理构造1—9级AHP判断矩阵B＝（bij）nxn，其中：

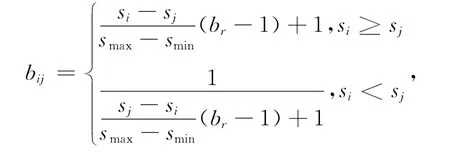
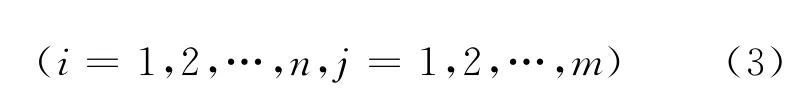
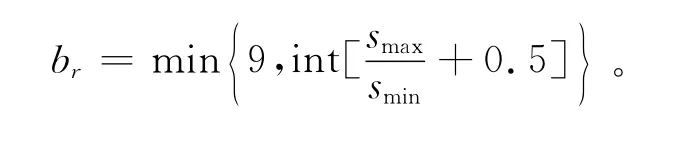
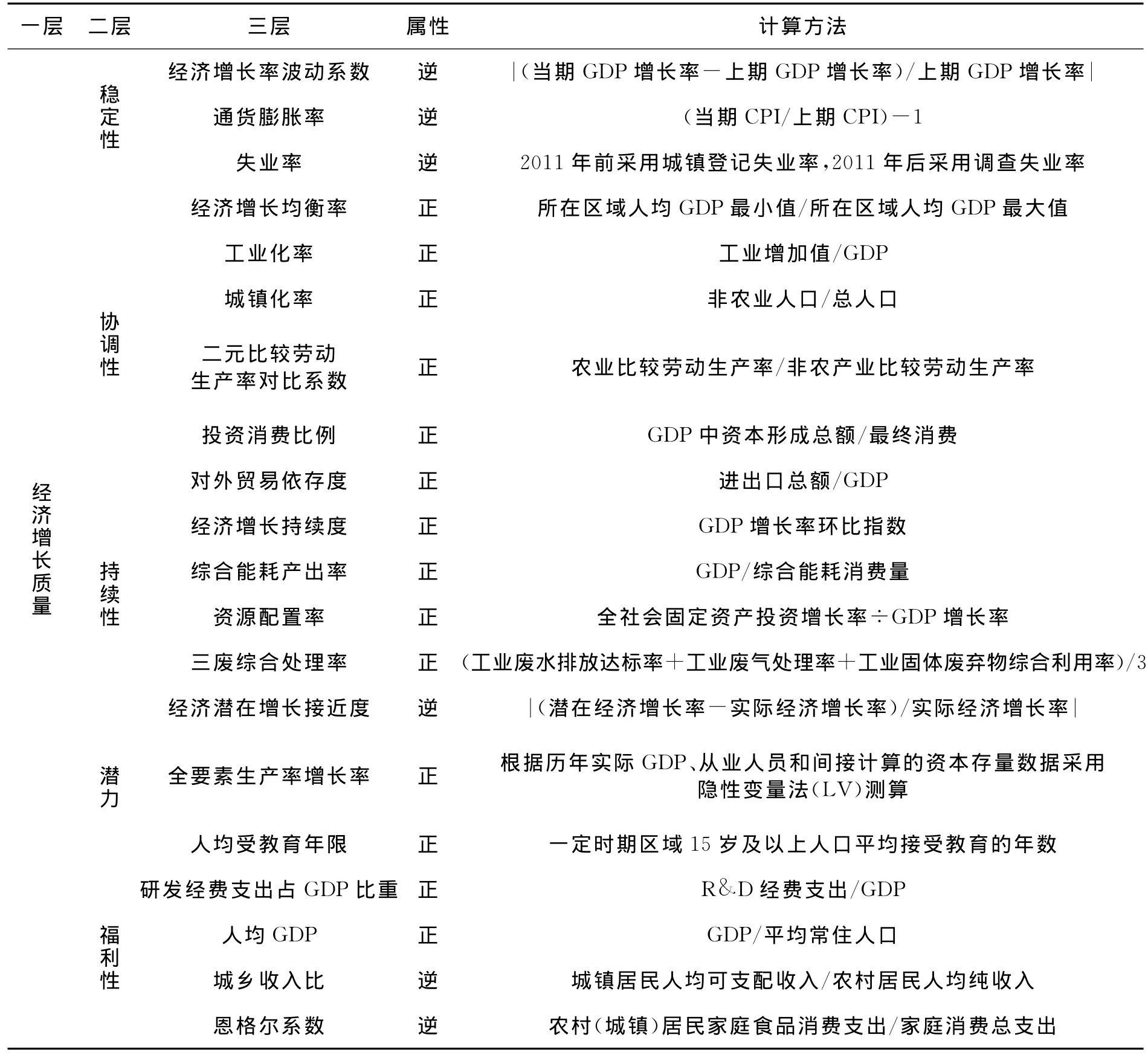
表1 区域经济增长质量综合分层评价指标体系

（三）寻优获得各评价指标权重

设判断矩阵B的修正判断矩阵为Y＝｛yij｝nxn，Y各要素的权重值为｛wi｜i＝1，2，…，n｝，则根据文献［9］的思想，使下式带约束的复杂多变量的目标函数达到最小的Y矩阵为B的最优一致性判断矩阵：

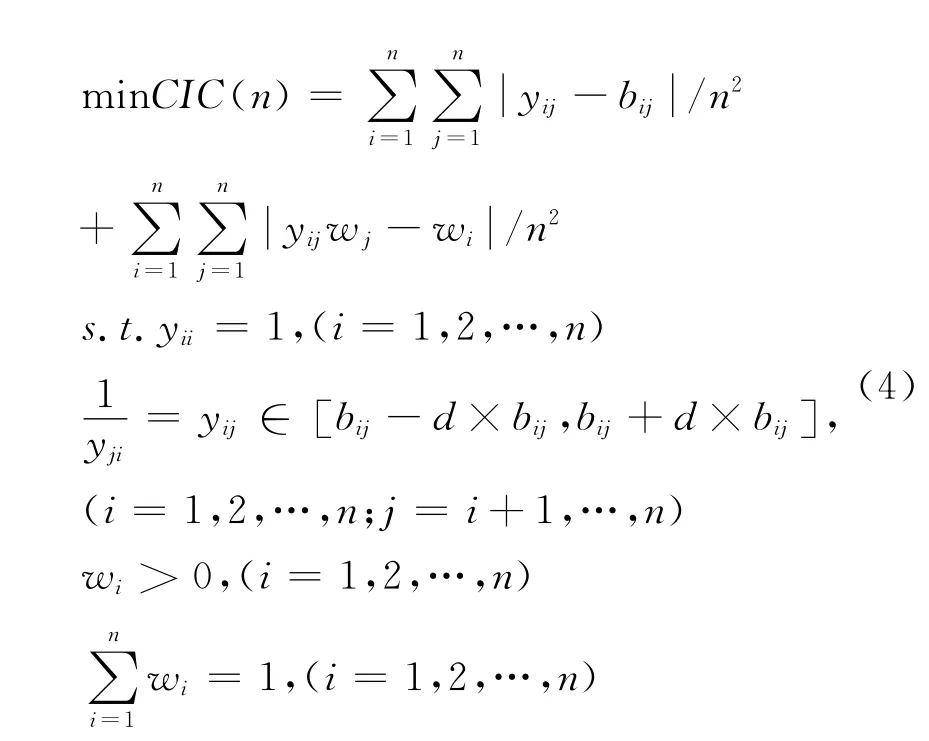
由计算实践可知，当满足Y为B的最优一致性判断矩阵时，也就是目标函数值（或者称为“一致性指标系数”）CIC（n）小于0.10时，会得到各评价指标的可以接受的权重值wi；0≤d≤0.5，一般取d值 为0.2，具体取值根据CIC（n）的大小进行调整。

（四）模糊综合评价值

由模糊综合评价矩阵R和优化运算算得到的各评价指标权重矩阵W＝（wi）n×1即可计算出各方案的模糊综合评价值：

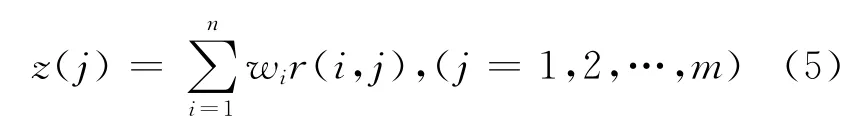
三、经济增长质量的实证分析

（一）数据来源及说明

以安徽省各地级市（因原巢湖市在2011年8月进行了规划调整，2002—2010年为17个地级市，2011年为16个地级市）为评价区域；样本时间为2002—2011年。

由于基础统计数据的连续性和可获得性原因，本文从构建的指标体系中选取了具有代表性的8个评价指标：经济增长率波动系数；城市化率（%）；二元比较劳动生产率对比系数；对外贸易依存度（%）；经济增长持续度；三废综合处理率（%）；经济潜在增长接近度；人均GDP（元/人），并分别以X1—X8为代码。

除X1和X7为逆指标外，其他6个指标均为正指标。原始统计数据选自安徽省统计局2003—2012年度的《安徽统计年鉴》。根据需要对相关基础数据经过了计算整理，其中潜在经济增长率是利用HP滤波法（平滑参数λ＝100）对各市现价GDP测算得到的。限于篇幅，在此略去各评价指标数据。

（二）综合评价集成模型运算

运用改进的AHP－FCE集成模型分别对论域进行综合评价的相关运算。在Matlab软件环境中，通过编程运算得到模糊综合评价矩阵R，据此构造改进的AHP判断矩阵B以优化获取各评价指标权重。优化方法采用模拟生物优胜劣汰机制的基于实数编码的加速遗传算法（Real coded based on Accelerating Genetic Algorithm，简称“RAGA”）程序，交叉概率取0.8，变异概率取0.2，种群规模为10，加速遗传运算次数为20次。由RAGA获得可以接受的各评价指标的权重值w后，通过R和w计算出样本时间内各区域的经济增长质量综合评价值z（j），结果见表2和表3。

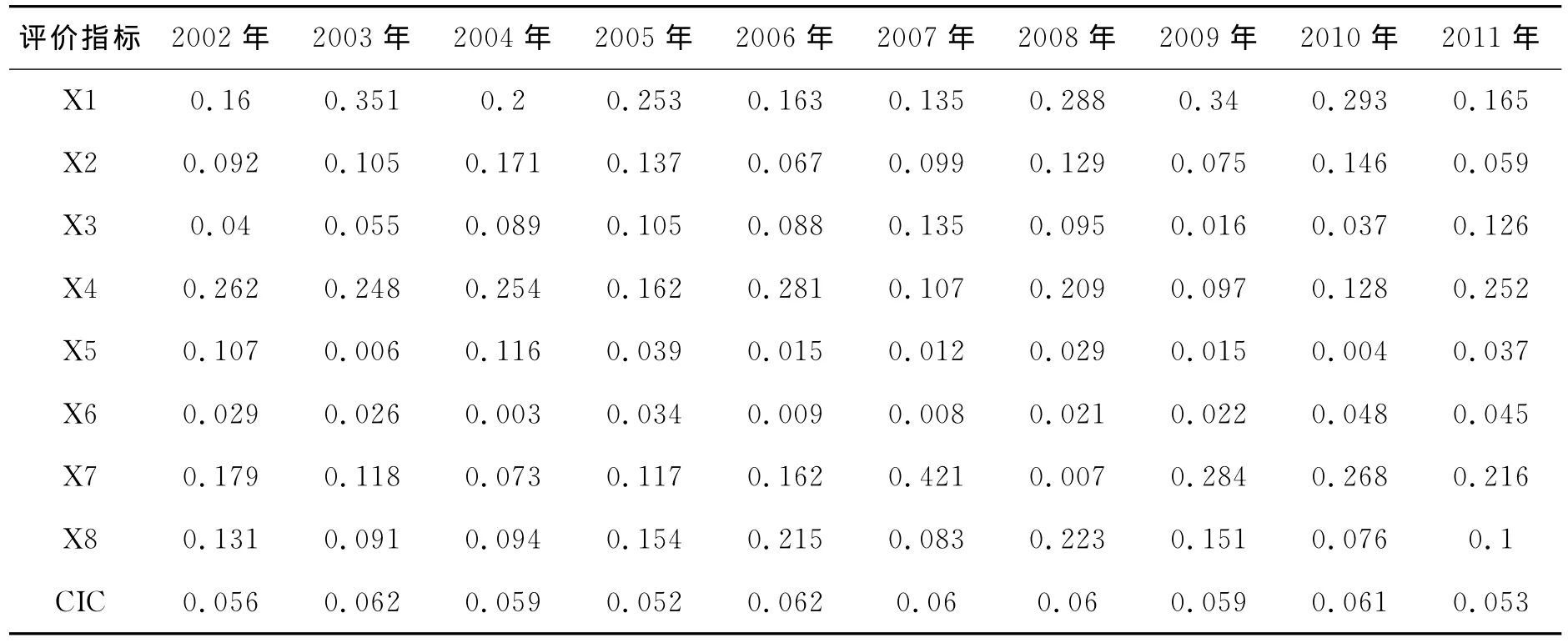
表2 2002—2011年各指标优化权重和判断一致性系数CIC

表3 2002—2011年安徽各市经济增长质量模糊综合评价值及排序

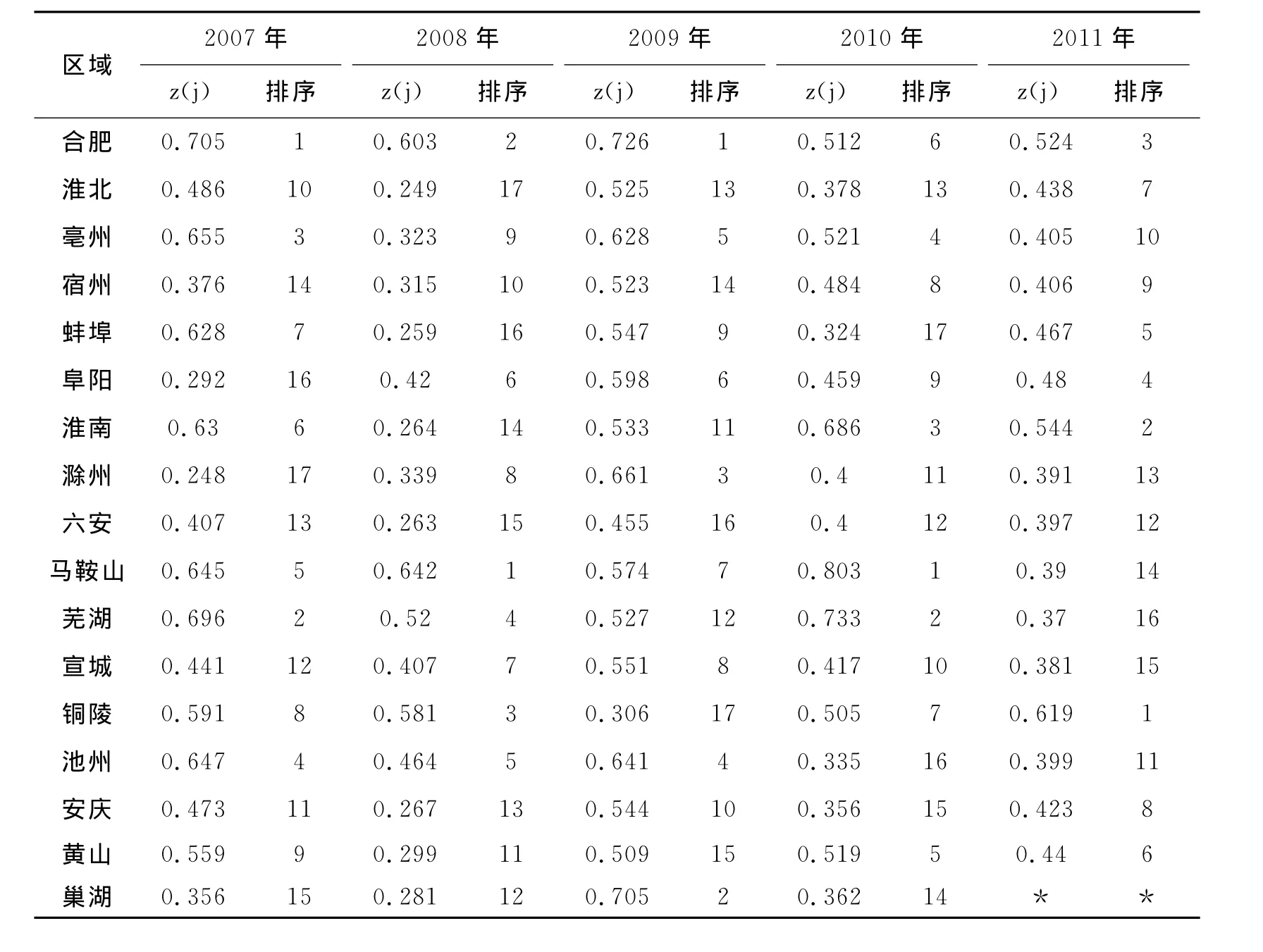
续表3

（三）结果分析

1.AHP判断矩阵一致性分析

由表2可知，安徽省各市由每年改进的AHP判断矩阵B而优化的目标函数值或判断一致性系数CIC（n）最小值：2002—2010年17市的CIC（8）分别为0.056，0.062，0.059，0.052，0.062，0.060，0.060，0.059，0.061；2011年16市的 CIC（8）为0.053，均小于0.10，表明样本期各年改进的AHP判断矩阵满足一致性要求，8个评价指标的权重是有效的。

2.市域经济增长质量综合评价值分析

由表3可知，2002—2011年安徽省各市经济增长质量综合评价值差异明显，这种波动特征由图1也可以直观看出。同时，从反映综合评价值变异程度的离散系数来看，样本期间内各年综合评价值的离散系数分别为 0.26，0.53，0.35，0.23，0.33，0.28，0.35，0.17，0.29，0.16，各年之间波动显著，其中2011年各市经济增长质量综合评价值变化幅度最小，离散系数只有0.16，而2003年各市变化幅度最大，离散系数为0.53；样本期间内各市（合肥、淮北、亳州、宿州、蚌埠、阜阳、淮南、滁州、六安、马鞍山、芜湖、宣城、铜陵、池州、安庆、黄山、巢湖）综合评价值的离散系数分别为0.13，0.23，0.41，0.33，0.28，0.34，0.29，0.29，0.24，0.19，0.19，0.16，0.24，0.32，0.21，0.18，0.29，各市之间变动幅度也存在显著差异，其中合肥市经济增长质量综合评价值变化程度最小，离散系数为0.13，而变化最大的是亳州市，离散系数为0.41。因此，样本期间各市经济增长质量综合评价值无论从横截面还从纵剖面来分析，均说明了8个指标测度的安徽省区域经济增长质量在10年间的动态变化轨迹和区域性差异。

图1 2002—2011年安徽市域经济增长质量综合评价值分布图

3.市域经济增长质量最大序差分析

为进一步分析安徽省各市样本期间经济增长质量综合评价值的差异，从评价结果排序角度引入“最大序差”［11］这一测度量来进行深入分析。

设ψjt为j市t年的经济增长质量综合评价结果的序次，于是该市最大序差ψmaxj为各年最大序次与最小序次之差，即：

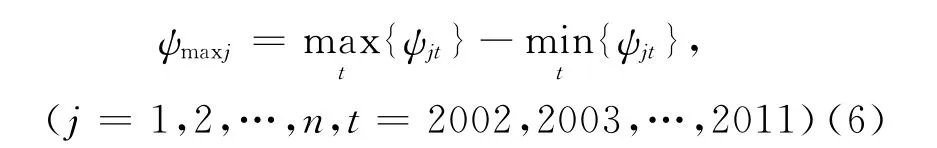
根据表3和式（6）计算出安徽省各市经济增长质量综合评价值的最大序差（表4）。数据表明，安徽省各市样本期间经济增长质量综合评价结果的最大序差相互之间变化较大，也印证了前述综合评价值的差异。

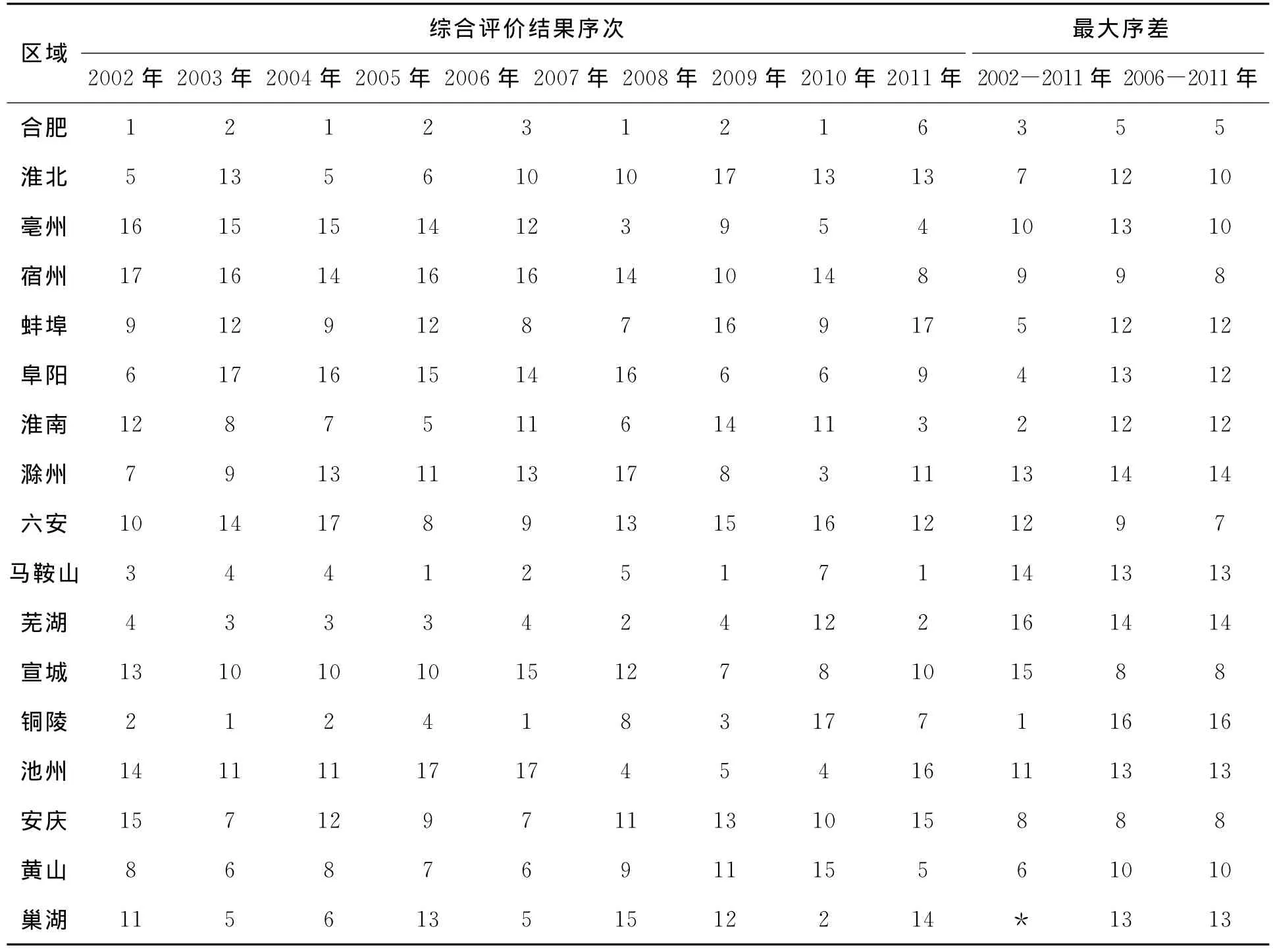
表4 2002—2011年安徽市域经济增长质量综合评价值序次和最大序差

若按最大序差的变化范围，可分成三类：稳定类（即ψmax≤5）、亚稳定类（即6≤ψmax≤8）和“跳跃”类。按此分类，得出各市的经济增长质量状况分类结果（表5和表6）。

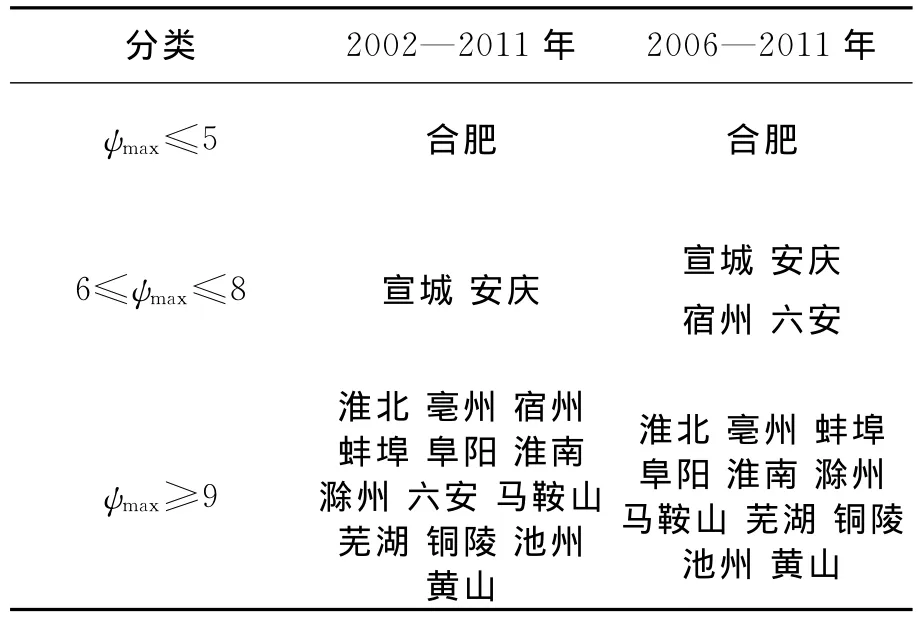
表5 安徽各市经济增长质量状况最大序差分类

4.市域经济增长质量影响因素分析

由表2可以看出，对安徽各市经济增长质量进行模糊描述的8个指标中，X1（经济增长率波动系数）和X4（对外贸易依存度）在样本期间的权重较大，因而对经济增长质量模糊综合评价值有较大的影响，也可以说明代表经济增长质量的稳定性和持续性是影响质量的主要因素。从代表经济增长质量五个维度（稳定性、协调性、持续性、潜力和福利性）的各个指标原始数据分析，各市经济增长率波动系数在样本期间有明显的周期性和差异性，在2006年前振幅较大，此后变化比较平稳，表明经济资源（劳动力、技术、投资等）周期性的变化发展导致了经济增长的波动，波动系数越小，经济越安全，而经济资源的效率逐步增强使得经济增长的质量有所提高；各市的城市化水平参差不齐，最高的铜陵市平均达到56.69%，而最低的亳州市平均只有10.86%，这意味着安徽城市化的发展空间巨大；各市的二元比较劳动生产率对比系数均在1.0以下，而且极差达到0.57，表明二元经济结构在生产率上偏差较大，相应地对经济增长质量的贡献较小，同时也证明城乡二元经济结构将在一定时期内继续存在，城乡统筹发展的任务紧迫；由于各市的资源禀赋、区位条件及经济发展水平的差异，其对外贸易依存度在各年间高低不同（如合肥市2003年高达51.51%，亳州市2004年只有0.59%），经济对外辐射能力存在强弱区别，因而对当地经济增长的贡献程度不一；2005年之前各市经济增长持续度变化较大且差异明显，此后差距缩小并渐趋平稳，表明经济增长的持续程度有所改善；各市彼此之间各年的三废综合处理率存在差幅，但每个城市的变化较为稳定，说明各市经济活动中污染产生的主要部门——工业部门处理三大污染的强度和综合利用水平有所加强；各市经济潜在增长接近度虽然波幅差异显著，但均处于经验值±50%范围内，可以认为现实经济增长既没有超出潜在经济增长一定程度而造成经济资源的效率损失，也未过低于潜在经济增长而造成经济资源的浪费，因而一定范围内经济增长的潜力对保持经济增长质量至为重要，也有利于降低经济运行的风险；人均GDP是反映经济增长福利性水平的主要测度指标，各市的具体数据显示：2002年最高人均GDP是最低的5倍，而2011年则不到5倍，样本期间年均人均GDP增长速度最高的达22.70%，最低的也有16.56%，因而可以说明各市经济增长的福利水平有一定的距离，但差距有逐渐缩小的趋势。从各个测度指标的分析可以得出，虽然其承载的信息各有不同、影响有大小之别，但综合起来对各维度经济增长质量的反映中，经济增长的稳定性和潜力较好而福利性、协调性和持续性较弱，具有一定的客观性和代表性，同时也有着很好的区分性。

表6 安徽各市经济增长质量状况最大序差区域分类

本文的综合评价是根据评价指标所提供的信息以及科学合理的集成模型进行的，各指标的赋权具有客观性，因而对安徽省各市经济增长质量的动态模糊综合评价结果是客观而可信的，总体上反映了“完善社会主义市场经济体制阶段”中10年（2002—2011年）的经济增长质量状况。从评价结果的分析中，我们可以得出两点结论：一是各市经济增长质量具有动态的区域性差异，经济增长质量稳定的核心区域较少，而皖北和皖南更多的城市则处于经济增长质量的“跳跃”状态；二是现有数据表明各市经济增长质量各维度发展程度不均衡：经济增长的稳定性和潜力要优于经济增长的福利性、协调性和持续性。因此，在安徽省后续的社会经济发展中，如何让更多的城市发挥后发优势进入到经济增长质量的核心区域、提升经济增长的福利性、持续性和缩小区域差距以整体提高经济增长质量并逐步实现经济强省目标是值得进一步认真思考的问题。

［1］毛健.经济增长理论探索［M］.北京：商务印书馆出版社，2009：86－98.

［2］陈海梁.论经济增长质量的内涵［J］.中国统计，2006（8）：56－57.

［3］任保平.以质量看待增长：对新中国经济增长质量的评价与反思［M］.北京：中国经济出版社，2010：55－62.

［4］张平.改革开放以来中国经济增长与结构变革［M］∥张平，王霞辉，王宏淼.中国经济增长前沿——转向结构均衡增长的理论和政策研究［M］.北京：中国社会科学出版社，2011：59.

［5］康英.青海省经济增长质量的评价与分析［J］.统计与决策，2009（15）：127－120.

［6］丁岳维，朱维敏，陈小霞，等.转型期西北地区经济增长质量评价研究［J］.河南社会科学，2011，19（1）：127－130.

［7］万力.关于贵州省经济增长质量的评价［J］.统计与决策，2008（8）：127－129.

［8］徐辉，杨志辉.密切值模型在经济增长质量综合评价计算中的应用［J］.统计与决策，2005（12）：22－23.

［9］金菊良，魏一鸣，丁晶.基于改进层次分析法的模糊综合评价模型［J］.水利学报，2004（3）：65－69.

［10］李荣富，傅懿兵，康乐.区域主导产业发展绩效的综合评价［J］.池州学院学报，2012（1）：65－70.

［11］郭亚军.综合评价理论、方法及应用［M］.北京：科学出版社，2007：126－129.