基于统计回归模型的突发事件网络舆情研究

●杨 畅，苏国强，兰月新，何永红

(武警学院，河北廊坊 065000)

(本栏责任编辑、校对 刘彦超)

1 现状分析

据CNNIC发布的《第33次中国互联网络发展状况统计报告》显示，截至2013年12月底，我国网民规模达6．18亿，全年共计新增网民5 358万人，互联网普及率为45．8%，较2012年底提升了3．7个百分点。与此同时，手机网民继续保持良好的增长态势，规模达到5亿，年增长率为19．1%，手机继续保持第一大上网终端的地位。［1］突发事件网络舆情，是指突发事件发生后，网民对于突发事件的意见、情绪和态度的总和。［2］突发事件发生后，人们通过互联网、新闻媒体报道、即时通讯工具等渠道能够在第一时间获取相关信息，并且利用网络这个平台表达各自的观点。由于突发事件的影响大，给人反应的时间短，容易滋生各种“小道消息”。如果不及时掌控突发事件网络舆情发展态势，并在适当时间进行有效干预，则可能造成突发事件事态扩大。例如，2011年初的日本核泄漏发生后，网络上就流传着核泄漏污染海洋影响食盐的消息，引发了国人的恐慌，导致各地市民疯狂抢盐。

近年来，国内外学者对突发事件舆情及其相关内容进行了研究。霍良安等以日本大地震为例，分析在突发事件中谣言的传播机理，探讨谣言传播的影响因素，寻找谣言泛滥的原因，剖析谣言传播的新特点。［3］张一文等在《网络舆情与非常规突发事件作用机制》中，利用系统动力学建模探究事物自身演化机理，为控制非常规突发事件网络舆情扩散，引导非常规突发事件舆情传播提供有力依据。［4］兰月新等在《突发事件网络舆情演进规律模型研究》中通过研究突发事件网络舆情形成过程及其影响因素，建立突发事件网络舆情演进规律的微分方程模型，确定舆情扩散过程中的三个特征时间点和舆情发展的四个时段，研究不同时段政府的应对策略。［5］研究网络舆情的发展动态，探索网络舆情的发展规律，有利于提升政府管理部门应对突发事件网络舆情的能力。本文在研究网络舆情传播特点的基础上，通过数学统计回归模型研究网络舆情的演化规律，以期为政府应对突发事件网络舆情提供思路。

2 突发事件网络舆情传播规律分析

2006年1月国务院颁布的《国家突发公共事件总体应急预案》规定:“根据突发公共事件的发生过程、性质和机理，突发公共事件主要分为自然灾害、事故灾难、公共卫生事件和社会安全事件。”突发事件发生的时间、规模及其发展趋势往往难以预测，并且带来较大的社会影响，突发事件网络舆情具有突发性、连锁性、关注性等特点。突发事件网络舆情传播阶段一般包括形成期、高潮期和消退期［6］，传播模式如图1所示。

由图1可知，突发事件网络舆情形成期的时间较短，事件发生后迅速攀升并达到舆情高潮，而消退阶段经历的时间比较长。突发事件发生后的第一时间里，网民通过新闻媒体、网络、即时通讯等媒介获得有关事件的文字、图片、音频、视频，并对事件进行讨论传播，投以自己的态度、情感、认知、观点、误解、猜疑。如果突发事件的真相得不到证实，网民就会有意无意地进行渲染甚至恶意炒作，使事情真相被歪曲。例如，湖北“石首事件”原本是一个青年厨师坠亡事件。然而，当地政府和相关部门消极应对，极力隐瞒真相、封锁消息。与此同时，网络上对该事件进行了失实“报道”。在这种情况下，当地政府仍然没有直面网民、平息民愤，导致网上舆论转化为网下行动，在短短一天时间内，引发了后果严重的群体性事件，致使事件处置起来更加棘手。因此，突发事件发生后，政府应该第一时间向公众公布事实真相，解除民众的疑惑，并对网络上的流言蜚语进行辟谣，控制舆情的走向，降低舆情高潮点。

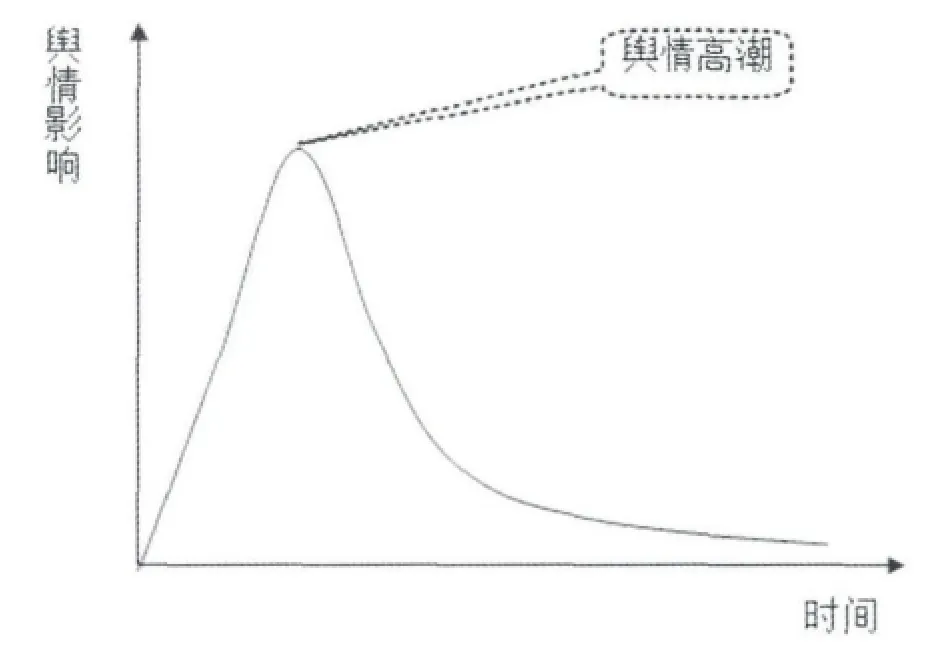
图1 突发事件网络舆情传播规律图

3 突发事件网络舆情传播模型

突发事件网络舆情从事件开始后迅速发展达到高潮，单纯从突发事件网络舆情影响与时间的传播规律来看，很难对其各个时间段的舆情增长情况进行研究。通过对舆情的新闻词频进行累加，可以引入统计回归模型来分析突发事件网络舆情的传播规律，如图2所示。

图2 新闻词频累加量与时间关系图

3．1 模型假设

设网络新闻词频累加量为y，传播的时间为x，二者之间的关系为y=f(x，β)，其中β为参数。由突发事件网络舆情的基本性质可知，新闻词频累加量与时间成正比;当时间较长时，新闻词频累加量渐进饱和，将趋于一个固定值。下面的模型具有这种性质:

Michaelis-Menten模型

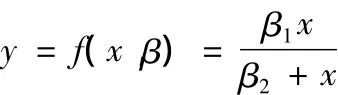
指数增长模型

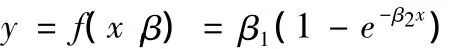
3．2 Michaelis-Menten 模型

上述模型对于参数β=(β1，β2)是非线性的，但是可以通过下面的变量代换化为线性模型

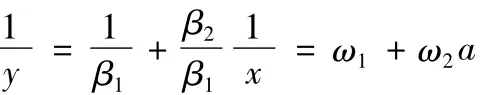
突发事件的网络舆情传播规律告诉我们，新闻词频最终累加量会受到各种因素的影响，比如政府对事件做出的回应、新闻媒体的报道、意见领袖的看法、网络炒作、网络谣言、网络推手等，都会影响舆情新闻词频的最终累加量，如图3所示。

图3 受影响的新闻词频累加量与时间关系图

为了考虑其他因素对突发事件网络舆情的影响，以下采用对原有模型附加增量的方法，来考察舆情的反应模型

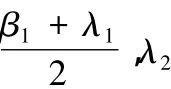
3．3 指数增长模型

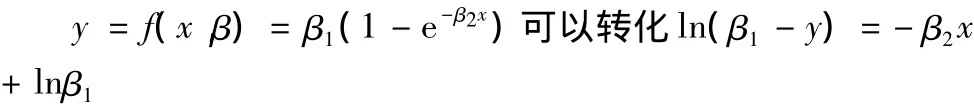
上述公式可以以时间x为横坐标，以ln(β1-y)为纵坐标，β1表示新闻词频最终累加量，当β1取不同值时有不同的拟合系数R，R越接近1，β1越接近实际值。

4 实证分析

笔者选取哈尔滨阳明滩大桥坍塌后的网络舆情作为研究对象，从而尝试验证突发事件网络舆情的传播规律。2012年8月24日早上5点30分左右，哈尔滨市阳明滩大桥一引桥发生坍塌，事发时有4辆货车停放在桥上。事故致使3人死亡，5人受伤。该桥总投资18．82亿元，原计划3年建成但仅耗时18个月。大桥于2011年11月6日竣工，距此次坍塌事故发生，通车时间仅9个月。就在事发当天，有媒体曝出“哈尔滨市建委有人说大桥指挥部解散了，找不到施工单位”。一时间舆论哗然，网上一片批评声。针对网民质疑，哈尔滨市25日召开新闻发布会回应“此事并不存在”。随后两天又对该事件进行回应，宣称该事故是由货车超重引起的，不属于施工质量问题。［7］来自网眼舆情研究中心的数据显示，之所以在8月24日出现舆情高潮是因为哈尔滨市政府没有在第一时间对该事件进行回应，8月25日民众初步了解该事件后，舆情呈下降趋势，如表1所示。

表1 哈尔滨阳明滩大桥坍塌事故中时间与新闻词频统计表

图4是经过累加后的哈尔滨阳明滩大桥坍塌新闻词频累加量与时间的关系。下面，笔者首先对该模型进行分析，然后探讨是否有更一般的模型来统一刻画该类事件，进而揭示其中的联系。

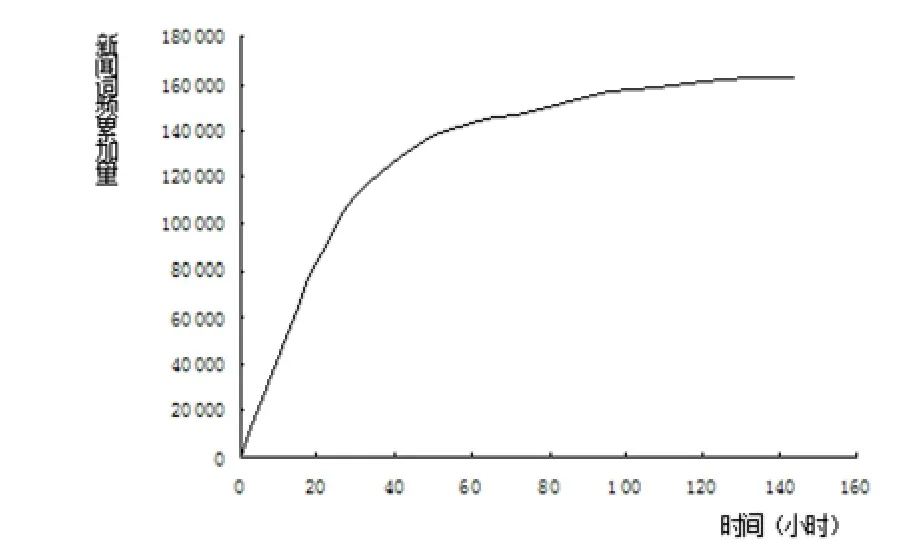
图4 哈尔滨阳明滩大桥坍塌事故新闻词频累加量图

4．1 Michaelis-Menten模型

上述模型对于参数β=(β1+λ1，β2+λ2)是非线性的，但是可以通过下面的变量代换化为线性模型

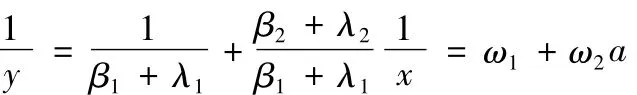
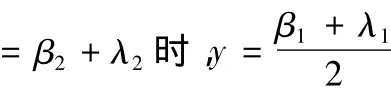
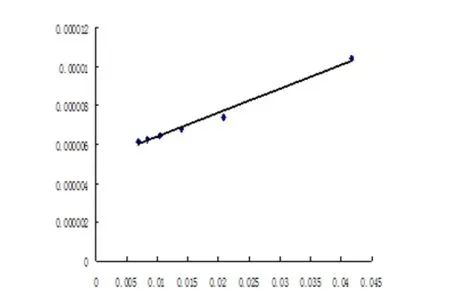
图5 的散点图和回归直线

表2 线性化模型参数的估计结果

4．2 指数增长模型

当β1取不同值时有不同的拟合系数R2，如表3所示。

表3 β1与R2的对应关系

取β1的值为β1≈165 350时，R2=0．994 7具有较高的拟合度，上述公式可简化为

以时间x为横坐标，以ln(165 350-y)为纵坐标，如图6所示。

图6 x与ln(165 350-y)的回归直线图

得出β2=0．029 2，利用指数增长模型对哈尔滨阳明滩大桥坍塌事件新闻词频累加量的数学模型可规划为

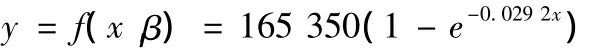
对y进行求导，可得y=165 350，所以该事件的新闻词频最大的累加量接近于165 350。

5 应对策略

无论是从突发事件传播规律还是从获得数据的分析来看，突发事件舆情与时间之间的关系都是非线性的，本文利用线性模型来简化参数估计。通过对哈尔滨阳明滩大桥坍塌事件舆情传播规律的分析研究，笔者认为对于突发事件网络舆情可采取以下应对策略。

5．1 公布权威信息

由上述模型可知，突发事件网络舆情发展期阶段时间短。据研究，社会上的突发事件一旦发生，一般2至3小时后就会在网络上出现，6小时后便会被多家网站转载，24小时后网上的跟帖和讨论就可以达到高潮。［8］可见，突发事件发生后，政府需要跟网络上的谣言进行竞争，要抢在谣言之前及时公布权威信息。政府公布的信息应该是比较全面的，能够客观地反映事实真相。如果政府公布的信息不完整，就容易被媒体和网民进行恶意串联，而引发更大的舆情，反而起到适得其反的效果。因此，政府应该建立一个快速高效的突发事件网络舆情反应机制，突发事件发生后能够适时恰当地公布权威信息，增强信息的公信力，避免信息媒体或网民歪曲地解读信息。

5．2 分析影响舆情的参数

在上述模型中，笔者重点分析了各个参数对舆情发展的影响。政府部门通过对突发事件舆情的参数作出相应的分析，就能提前获知突发事件舆情发展的规律，就能尽早地采取应对措施。由上述的舆情传播数学模型可知，突发事件舆情的最终累计量为β1，降低舆情影响的关键在于降低β1。采用Michaelis-Menten的混合模型时关键是要把握住λ1，如果λ1为负数，则舆情有所降低;如果λ1为正数，则舆情有所上升。在对突发事件舆情进行研判时要注意这几个参数，尽早采取措施来降低其对舆情的影响。

5．3 完善监测系统

舆情的监测是利用计算机软件，采用网络数据信息挖掘、网络内容动态分析等方法，对网络上出现的网民关于事件的一些态度和讨论进行监测。在突发事件发生后，可以通过对该事件在网络上引发的舆情进行分析，建立起上述的数学模型。这个数学模型是对舆情的一种预测，当将监测到的舆情与构建的数学模型进行对比时就可以发现差异。这样就能制定更好的策略来缩小之间的差异，使舆情的发展始终处于可控范围内。与此同时，通过对突发事件网络舆情的监测，还可对网络舆情的整体发展趋势作出预先的判断。舆情监测要运用具体可行的方法来量化和分析，最终做到指标体系完整，内容准确有效，设计合理科学。

［1］中国互联网络信息中心．第33次中国互联网络发展状况调查统计报告［EB/OL］．(2014-03-02)．http://www．cnnic．net．cn/hlwfzyj/hlwxzbg/hlwtjbg/201403/t20140305_46240．htm．

［2］喻发胜，王晓红，陈波．网络传播的衍生效应与网络舆论［J］．湖北社会科学，2010，(5):179-181．

［3］霍良安，黄培清．突发事件中的谣言传播问题研究［J］．情报杂志，2011，(10):77-81．

［4］朱恒民，李青．面向话题衍生性的微博网络舆情传播模型研究［J］．现代图书情报技术，2012，(5):60-64．

［5］兰月新，邓新元．突发事件网络舆情演进规律模型研究［J］．情报杂志，2011，(8):47-50．

［6］陈烨．突发事件中的网络谣言传播研究［D］．武汉:华中师范大学，2010．

［7］8·24哈尔滨阳明滩大桥坍塌事故［EB/OL］．(2013-06-24)．http://baike．baidu．com/link?url=gJ_1ivQtl3iCU7IPb04srg7rq 6j3zWDKElV5D7ykewGeNnK-EshpZpX95laXbTaAlY_3R5VySj18 k7ovMopzNK#1．

［8］姜胜洪．网络舆情热点的形成与发展、现状及舆论引导［J］．理论月刊，2008，(4):34-36．