基于替代路径的军事物流运输网络连通可靠性评价

缪子山

(驻南昌铁路局福州军代处，福州355013)

军事物流是指军事物资经由采购、运输、储存、包装、维修保养、配送等环节，最终抵达部队用户而被消耗，从而实现空间转移的全过程［1］。军事物流是将国民经济转化为军事战斗力的桥梁和纽带，是保障战争胜利的主力军。现代军事物流的基本要求是“快速、可靠、安全、高效、经济”，而可靠性是最直接的影响因素。战争中的不确定因素难以预计，作为直接维持战争持续的军事物流系统，其面临多变战况时运转的可靠性也成为决定战局成败的关键因素之一。因此，只有保证运输网络的可靠性才能为军队建设和作战提供有力的运输保障，才能保障军事物流安全、准确、及时、高效地运行。

对军事物流运输网络可能造成干扰或破坏的因素很多，包括自然、人为灾害或事件，如地震、洪水、恐怖袭击、军事打击、异常天气等。虽然发生这些事件的规模、影响范围、频率、可预见性各有不同，也是不能完全避免的，但通过对军事物流运输网络的可靠性进行评价并以此为基础采取相应的应对措施，可以降低事件对军事物流运输网络造成干扰和破坏的程度。

1 军事物流运输网络连通可靠性的定义

可靠性是一种概率型测度指标，它反映的是各种自然灾害和人为事件带来的网络不确定性，反映了军事物流运输网络状态的波动程度和处理该波动性的能力。军事物流对可靠性的要求很高，而运输是军事物流活动的核心内容，运输网络的可靠性直接决定了军事物流的可靠性。军事物流运输网络的可靠性包含连通可靠性、流量可靠性、时间可靠性、成本可靠性、遭遇可靠性等。在战争时期或遇到灾害时，人们关心的往往是军事物资是否可以顺利抵达目的地，连通性是最基本也是最重要的要求，即网络的连通性指标是可靠性研究的基础。

连通可靠性本质是反映物流运输网络在灾害或战争等突发事件导致部分路径断开或容量衰退的情况下剩余网络继续承担物流运输功能的能力，它着重反映物流运输网络在拓扑结构或者是供给上承受冲击、破坏的能力。军事物流中对运输网络的抗破坏能力要求更高，在战争条件下必须保障军事物流运输网络的畅通，保证运输网络的连通可靠性。因此，连通可靠性是军事运输网络可靠性的首要评价指标，具有不可替代的地位。

连通可靠性描述了网络节点之间是否连通，即是否至少存在一条路径连通。对于军事物流运输网络而言，如果网络中的每一对OD 之间都存在一条路径连通，那么整个军事物流运输网络就是连通的。军事物流运输网络连通可靠性描述了军事物流运输网络节点之间保持连通的概率，它可以定义为在现有军事物流运输网络的运行条件下，在军事运输条件和费用允许的基础上，军事物流运输网络中任意2 个节点之间至少存在一条路径连通的概率。它是最简单、最基础的军事物流运输网络可靠性评价指标，最能适应在战争、突发灾害等异常情况下对军事物流运输网络基本能力的评价。

目前，国内外评价可靠性的方法主要有终端可靠性评价方法［2］、博弈论技术［3］、蒙特卡罗方法［4］、吸收马尔科夫链方法［5］和微观交通仿真技术［6］5 种。基于这5 种方法，近年来又衍生出一些新的、具体的计算网络连通可靠性的方法，如基于替代路径的连通可靠性评价方法，基于关键点段的连通可靠性评价方法等。通过对大量资料的查询和各种可靠性评价方法的比较分析，本文采用基于替代路径的连通可靠性评价方法［7］，并结合军事物流运输网络的特征对军事物流运输网络的连通可靠性作出评价。

2 基于替代路径的连通可靠性评价方法

2.1 算法思路

基于替代路径的连通可靠性评价方法在对军事物流运输网络的某路段进行分析时，只考虑2种状态，即路段连通或者中断，不考虑路段通行能力的限制。对网络的连通性进行分析时，首先要识别每个路段的状态，给其赋值0 或1。例如，路段i连通则路段i的状态xi赋值为1，否则赋值为0，即

在对军事物流运输网络状态进行分析的基础上，可以计算运输网络的连通性ri，ri是运输网络状态xi的数学期望，即

计算军事物流运输网络连通性有2 种方法:一种是将军事物流运输网络看作是大量路段的结合，进行统计分析;另一种是将军事物流运输网络看作整体，不考虑路段状态，给出网络状态赋值。即

同理，可以计算出运输网络的连通性为

连通性是最简单、最基础的军事物流运输网络可靠性评价指标，连通性是网络可靠性研究的基础，它直观地反映了军事物流运输网络的拓扑结构。它的优点是计算简单，计算所需要的数据少，可以通过便捷的数学运算对整个军事物流运输网络的连通性进行直接计算。但是，连通性衡量方式存在本质上的不足，因为它只允许两种状态存在，要么连通要么中断。因此，对于军事物流运输网络上的运输状态处于连通或中断这2 种极端情况之间的状态无法描述。连通性比较适用于特殊情况下，如战争或地震等灾害发生时的军事物流运输网络状态评价。

伴随着我国军事物流的快速发展，传统的连通性评价方法己经很难准确评价军事物流运输网络的可靠性。在实际情况下，军事物流运输网络很少是由于拥堵、事故、施工等原因导致运输网络的破坏，而更多地是考虑遭受军事打击或其他自然灾害的破坏。因此，更实际地是判断在最理想出行路径被破坏时，是否存在合适的替代路径。而对于一个运输OD，如果替代路径与原路径的运输费用差别较大或者大于可以承受的能力和范围，那么这个运输网络是不能够满足军事物流需求的。另外，对于某一OD，虽然运输选择的路径很多，但大多数路径可能共用某一路段，当这一路段断开，则较多路径被破坏，或者某些路径有较多的重复路段，其中一个路段断开影响较多路径的概率更大，这样的军事物流运输网络在连通性上也是不可靠的。

基于以上的认识，本文采用这种基于替代路径的连通可靠性评价方法，其基本思路是:①替代路径与原始路径的运输费用差距越大，可靠性越低;②最优路径中，不可替代的路段越多，可靠性越低;③运输费用与原始路径相差较小的路径即次优路径，与原始路径共用的路段数越多，则可靠性越低。

2.2 计算公式

根据上述思路，得出针对任意一个OD 对之间连通性的算法为

式中:φ(ODi)为第i个OD 对之间的连通可靠性;f(l)为路径l的运输费用;lz、lt分别为该OD对间的最优路径和替代路径(替代路径是指在OD 对之间，排除最优路径所用路段以外其他路段组成的最优路径);nz为最优路径所覆盖的总路段数;nb为最优路径上不可替换的路段数;ng为运输费用与最优路径相差较小的路径与最优路径共用的路段数;α 为修正系数，它反映了替代路径和最优路径的出行费用对连通性的影响权重，本文推荐取值为1;β 为修正系数，它反映了最优路径中不可替换的路段数对连通性的影响权重，本文推荐取值为2;γ 为修正系数，它反映了出行费用增长最少的替代路径，即次优路径和最优路径共用的路段数对连通性的影响权重，本文推荐取值为0.5。

在军事物流运输网络中任意一个OD 对之间运输费用最少或选择可能性最大的路径为最优路径。运输费用是决定军事物流运输网络连通可靠性评价的决定因素。由于军事物流运输网络的连通性仅考虑运输网络的拓扑结构，因此运输费用函数可用路径的长度表示。

3 实例分析

3.1 物流运输网络的表示方法

以军事物流运输网络中的道路交通运输网络为例进行实例分析。道路运输网络由大量的街道和交叉口组成，将交通运输网络抽象和简化成图论中的网，是研究交通运输网络的基础和关键。图论中有关图的基本概念如下。

(1)图。一个图是由一些点及这些点之间的连线(不带箭头或带箭头)所组成的。为了区别，把两点之间不带箭头的连线称为边，带箭头的称为弧。如果一个图所有连线都是边，称为无向图;如果一个图所有连线都是弧，则称为有向图。

(2)连通图。若一个图中任何两点之间，至少有一条链(或路)，则为连通图。

(3)赋权图。如果图中的每一条边(或弧)都对应着一个数用于表示与这条边有关的数量指标，则这样的图为赋权图。

表示军事物流道路运输网络通常是用图论中的赋权图。节点一般代表路网中道路的交叉口或物流网络的重要节点，连线代表在两点之间存在一条路径。但需要注意的是，这种连线并不包含路径的通行能力或道路的形状、宽度等信息。实际道路运输网络中无论是路段的数目还是交叉口的数目都是巨大的，如果将这种实际道路一一对应地转换成计算网络，一方面收集整理相应的数据十分困难，另一方面计算时间将成倍增加。因此，根据需要对实际道路运输网络进行适当简化。

简化时考虑以下因素［8］:①窄而通行能力小的道路可以不予考虑，主要考虑通行能力较大的路段;②小的道路交叉口或物流节点可以不作节点考虑，主要考虑较大的道路交叉口或物流节点;③根据需要可将几条平行道路合并成一条道路，并修改这条道路的通行能力。军事物流运输网络图的表示方法并不是唯一的，对节点和路径的定义以及简化的原则不同所得的网络图也会不同。

3.2 连接两机场的道路运输网络描述

虹桥机场位于上海市西郊，距市中心仅13 km。浦东国际机场位于上海长江入海口南岸的滨海地带，占地50 多km2，距上海市中心约30 km，距虹桥机场约40 km。目前，虹桥机场主要负责国内航班而国际航班都在浦东机场。作为华东地区最大的两个机场，研究连接两机场的运输网络可靠性具有一定的军事意义。

根据3.1 图论中对路网的描述，需要将实际路网简化成图论中的网，并根据需要对实际的道路运输网络进行必要的简化。在计算连通可靠性时，不考虑路径的实际通行能力或道路的形状、宽度等信息，运输费用函数选用路径的长度来表示。

由于连接两个机场的道路运输网络无论是路段的数目还是交叉口的数目都十分巨大，根据需要对实际道路运输网络进行适当简化。根据上文提出的3 点简化原则，以道路的长度作为运输费用，可得到简化后的路网拓扑图(如图1 所示)。为使拓扑图更加形象，本文适当保持了实际路网的形状。

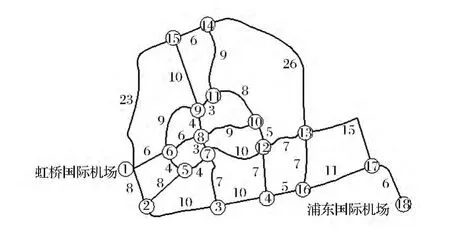
图1 连接两机场的道路交通网络拓扑图(km)

图1 中，节点1 代表虹桥国际机场，节点18 代表浦东国际机场，节点1 和节点18 构成一个OD对，相邻两节点间的数字表示该路段的长度即该路段的运输费用，下面根据该路网拓扑图进行连通可靠性计算。

3.3 网络连通可靠性计算

(1)寻找最优路径。按照有向图的搜索方法，根据各路段的出行费用，找出连接OD 的最优路径。如图1 所示，最优路径为“1—2—3—4—16—17—18”(称lz)，覆盖路段数nz=6，出行费用f(lz)=50。其余的路径为“1—6—5—7—12—13—17—18”“1—6—5—7—3—4—16—17—18”“1—2—5—7—12—13—17—18”，对应的出行费用分别为52、53、58。

(2)假设最优路径被破坏。假设最优路径所经过的路段均不可用，即令最优路径覆盖路段的出行费用均为正无穷大M。这里需要说明的是路径“17—18”为浦东机场与外界连通的主干道，通行能力较大，出现拥挤的可能性不大，因此将该路段继续作为可用路段。按照该方法对图1 进行修改，得到最优路径被破坏后的网络拓扑图(如图2所示)。

图2 最优路径破坏后的网络拓扑图(km)

(3)重新寻找新网络的最优路径，即原网络的替代路径。对照图2，寻找到最优替代路径为“1—6—5—7—12—13—17—18”，f(lt)=52。

(4)判断最优路径lz上的不可替换路段数。处理步骤:令lz所覆盖路段的出行费用为M。逐一判断lz所覆盖路段的可替代性。对于任意路段(如l2-3)，当其断开时，即l2-3的出行费用为M时，搜索网络上的新最优路径lz2-3，如果lz2-3的出行费用0 ＜f(lz(2-3))＜M，即可以找到一个替换路径，并且没有经过lz所覆盖的路段，则对于lz来说l2-3可被替换，例如图2 中的l1-2、l2-3、l3-4、l4-16和l16-17可被替换。如果lz(2-3)的出行费用f(lz(2-3))=M，即替代路径必须经过lz所覆盖的路段，则对于lz来说，l2-3不可以被替换，例如图2 中的l17-18。如此可以判断每个lz覆盖路段的可替换性，将所有不可被替换的路段数进行汇总，得不可替换路段数nb=1。

(5)寻找出行费用增长最少的替代路径，即次优路径。对照图2，寻找到次优路径为“1—6—5—7—12—13—17—18”，它与最优路径lz共用了路径“17—18”，可以得出共用路径数ng=1。按照式(3)计算OD1-18间连通性为

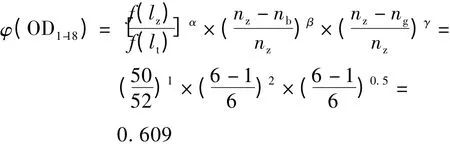
按照上述方法，利用基于替代路径的运输网络连通可靠性算法可以简便地计算出任意OD 对之间的连通可靠性，随之求出整个运输网络的连通可靠性。但是随着交通运输网络的增大，计算也越来越复杂，其难度也越来越高，相关参数和出行费用的确定仍需要进一步的探讨。

通过对路网具体数据的采集计算得连接虹桥机场与浦东机场路网的连通可靠性为0.609，具有较好的连通可靠性。由于影响军事物流运输网络连通可靠性的因素众多，网络的连通可靠性评价指标的算法和相关参数还有待进一步改进。另外，本文提出的算法，其可靠性评估是针对某一OD 对和运输路径，对实际的大规模军事物流运输网络整体进行可靠性评价还有待进一步研究。

4 结 语

本文在借鉴路网连通可靠性研究成果的基础上，结合军事物流的实际，对军事物流运输网络连通可靠性进行定义，给出了基于替代路径的军事物流运输网络连通可靠性算法，并以连接上海虹桥机场和浦东机场的交通运输网络进行实例分析，得出了该运输网络连通可靠性较好的结论。但是，对军事物流运输网络可靠性的研究是一个系统的过程，本文的研究还远不足以解决军事物流运输网络可靠性的众多问题。军事物流运输有待进一步研究的内容还有很多，如海陆空等多种运输方式在军事运输网络中的相互衔接，大规模军事运输网络可靠性的研究，整个军事物流运输系统的可靠性研究，不确定条件下的军事物流可靠性分析，军事物流与地方物流的有效结合等。

［1］ 王宗喜，徐东. 军事物流学［M］. 北京:清华大学出版社，2007.

［2］ 范海雁，吴志周，杨晓光. 基于道路交通网络拓扑结构的可靠性研究［J］.中国矿业大学学报，2005，34(4):482-485.

［3］ Bonsall P W.Travelers’response to uncertainty［G］//Bell M G H，Cassir C. Reliability of Transport Network. UK:Research Studies Press，2000:1-10.

［4］ Bell M G，Iida Y.Transportation Network Analysis［M］.Chichester:Wiley (John)＆ Sons，1997.

［5］ Bell M O. Computing network reliability［J］. Operation Research，1979，27(4):823-838.

［6］ National Research Council (U. S.). Transportation networks modeling［C］//Transportation Research Board Meeting. Washington D.C.:National Academy Press，1999:485-499.

［7］ 衡玉明.城市公交网络可靠性研究［D］. 北京:北京交通大学，2006.

［8］ 刘海旭.城市交通网络可靠性研究［D］. 西安:西南交通大学，2004.