基于集对势的车辆野战维修装备编配方案优选方法

王亚鹏，张巾帼，薛元飞，王春杰，李太慧

(1.军事交通学院 装备保障系，天津300161;2.军事交通学院 基础部，天津300161;3.军事交通学院 科研部，天津300161;4.71521 部队，河南 新乡453002;5.73055 部队，江苏 江阴214432)

为了保证车辆野战维修装备能与车辆装备整体配套、功能衔接、数量适当，切实发挥其维修保障效能，必须预先制订多套可选、合理完善、各有侧重的车辆野战维修装备编配应用方案。通过文献检索发现，目前对(车辆)野战维修装备编配方案优选或评价的研究相对较少，且都是运用熵权法、双基点法(TOPSIS 法)对战时车辆野战维修装备编配预案进行评价优选［1-3］，这些方法虽然预期效果比较理想，但其建模过程繁琐，公式计算复杂，操作使用不便。鉴于此，本文采用集对势理论［4］构建一个新的车辆野战维修装备编配方案优选模型，为车辆装备指挥员提供有价值的决策依据和参考指导。

1 战时车辆野战维修装备编配方案优选指标体系

为便于对比分析，主要借鉴文献［3］的研究成果构建指标体系(如图1 所示)。

图1 车辆野战维修装备编配方案优选指标体系

(1)维修作业能力。主要指各种野战维修装备维修作业能力的整体效能，它是应用方案中最重要的选优指标，是完成各种任务基本前提保证。维修能力性越强，应用方案可行性越高。

(2)功能衔接性。主要指为形成全过程的保障能力，将功能互补的维修装备进行联合使用的过程。通过各种不同功能的野战维修装备有效衔接，共同完成维修保障任务。在应用方案中，各种野战维修装备的功能要尽可能互补。

(3)保障经费合理性。不同的应用方案将导致部队保障费用不同，在保障完成任务的前提下，使用保障费用越少，方案合理性越好。

(4)种类配套性。主要是考虑各种野战维修装备的应用比例，应用方案必须做到整体配套合理，才能使部队的车辆野战维修装备综合保障能力提高。野战维修装备应用比例越合理，方案的配套性越高。

(5)战术性能先进性。不同的应用方案，野战维修装备总体的战术性能不同。车辆野战维修装备战场生存能力、隐蔽性能等战术性能越高，完成保障任务的能力越强。

(6)技术性能先进性。在执行保障任务时，机动性、可靠性和可操作性等越好，车辆野战维修装备的总体效能就越好。

显然，上述指标均为定性指标，量化数据获取较为困难，客观上增加了评价优选的难度和不确定性。为便于操作实施，拟先采用专家打分法对每个车辆野战维修装备编配方案各单项指标进行初步打分评判，在此基础上运用集对势模型对车辆野战维修装备编配方案进行综合评价优选。

2 车辆野战维修装备编配方案优选模型

2.1 集对分析及集对势

集对分析(set pair analysis，SPA)是我国学者赵克勤先生提出的，是研究2 个或多个事物同异反联系和转化的一种系统数学方法［4］，其核心是将系统内的确定性和不确定性予以辨证地分析和数学处理，并将不确定性和确定性作为一个系统进行综合考察。它将系统的确定性分为“同一”与“对立”两个方面，将不确定性定义为“差异”，三者相互联系、相互制约，并在一定条件下相互转化。

集对分析的基本概念是集对及其联系度。集对是指具有一定联系的2 个集合所组成的对子。联系度是对集对在某一特性的联系的定量刻画，其表达式为

式中:a、b、c为非负实数，依次为同一度、差异度和对立度，且a、b、c三者的统一形成两集合联系度的整体，即a+b+c=1;i、j分别为差异度和对立度的相应系数，一般规定i∈［-1，1］，j=-1［4］。

当c≠0 时，同一度a与对立度c的比值a/c称为所论集对在指定问题背景下的集对势，用“shi”表示［4］，记为

当c≠0 时，算得的集对势是相对确定的，若a/c＞1，称为集对的同势，若a/c＜1，称为集对的反势，若a/c=1，称为集对的均势;当c=0 时，式(1)的值变得无穷大，这时若b≠0，则可以考察a/b的值，并看作是c=0 情况下的集对势，由于b的相对不确定性，这时的集对势是相对不确定的。根据a、b、c的大小关系，集对势存在一定的次序关系［4］，见表1。

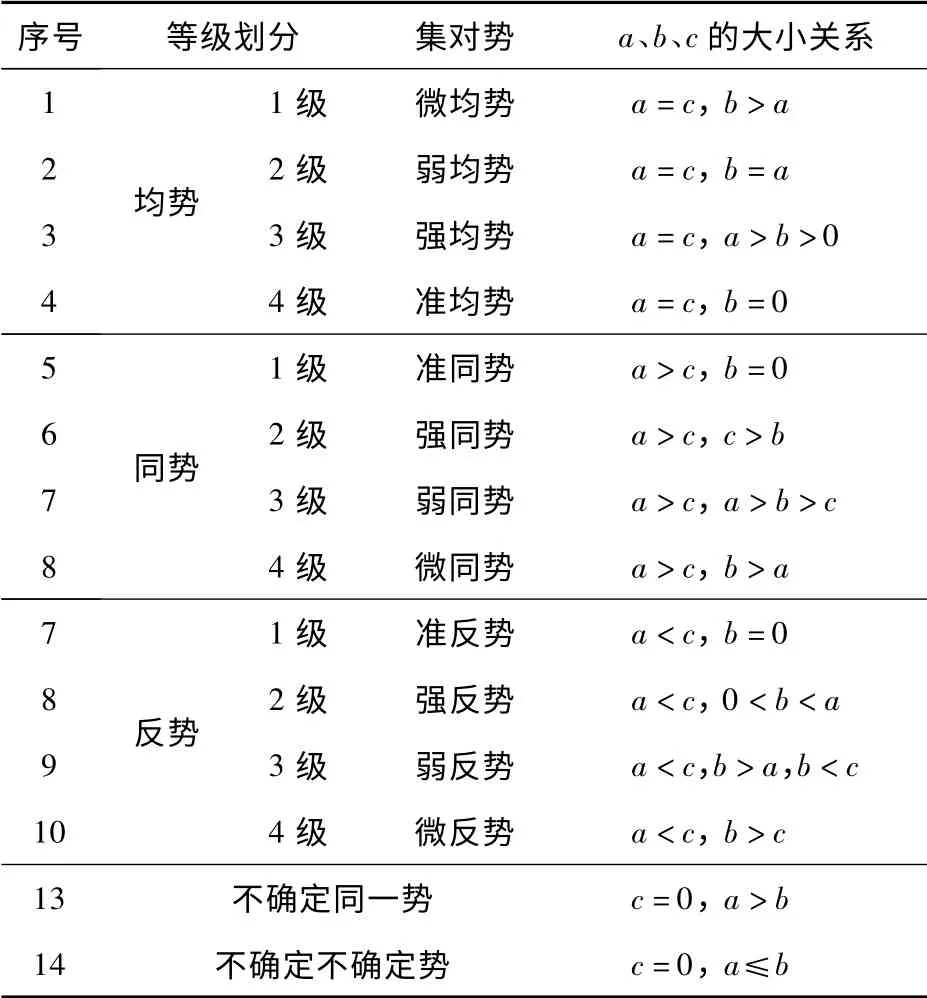
表1 集对势等级与次序关系

2.2 基于集对势的车辆野战维修装备编配方案优选模型

车辆野战维修装备编配方案优选可以看作是一个由决策者、优选方法和优选对象组成的系统。运用集对分析理论研究车辆野战维修装备编配方案优选过程，可以找出很多集对，如决策者和备选方案、评价者和评价对象、评价指标和评价标准等。

车辆野战维修装备编配应用方案优选本质上是决策者对多个备选方案横向对比择优而用的问题。其决策过程是决策者结合评价专家对各备选方案的评判分析，再通过对各备选方案中单项指标之间的对比分析，以及与客观评价标准的对照分析，综合考量最终得出最优方案。因此，决策者和备选方案所构成的集对是所要研究的核心集对，其他集对是辅助集对。

2.2.1 确定问题域

为了便于方法对比仍采用文献［3］中的问题背景。战时某摩步师执行跨区机动保障任务，战前制订N套车辆野战维修装备编配应用方案，其内容主要包括:该部队车辆野战维修装备的种类、数量、人员以及装备补充等，记为X=(X1，X2，…，Xn)，Xn为第n个待评价方案;评价指标集为U=(U1，U2，…，Um);指标权重为W= (W1，W2，…，

2.2.2 确定指标联系度

按照百分制标准，请车辆装备保障相关专家对车辆野战维修装备编配方案的各单项指标进行打分评判。假设某位专家对某方案的某个指标评判为65 分，根据集对分析理论，则可认为其余失掉的35 分处于对立趋势，其联系度可表示为μ =65 +35j(此时认为bi项中b=0)。根据专家打分情况［3］，可得车辆野战维修装备编配方案指标的联系度(见表2)。

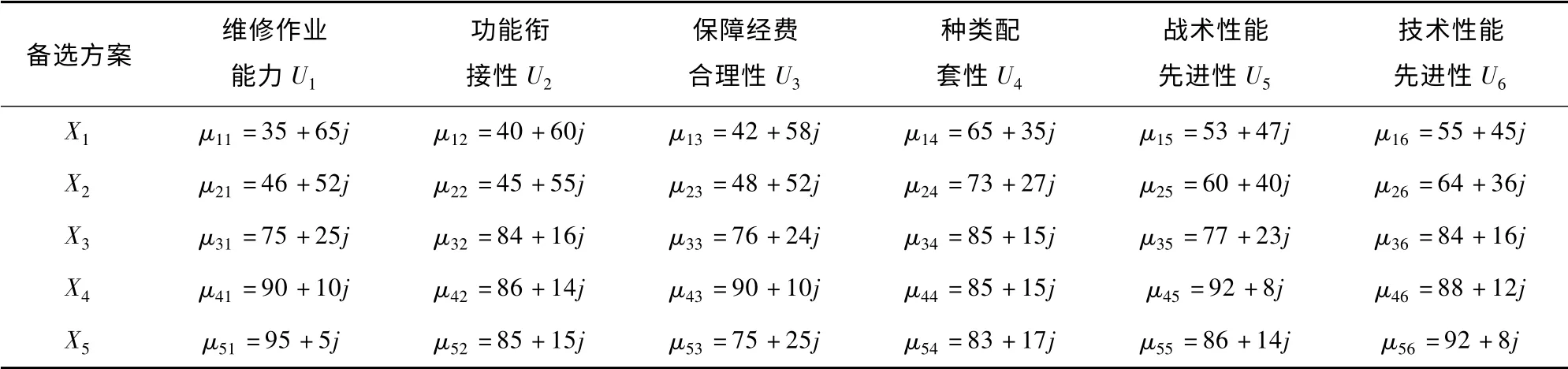
表2 车辆野战维修装备编配待选方案中各指标的联系度

2.2.3 确定指标权重

权重既是各因素本身物理属性的客观反映，又是决策者的客观评价，是主、客观综合量度的结果。确定指标权重的方法有很多，有德尔菲法、相对比较法、最小平方法、层次分析法、熵权法等［5］。为了确保数据统一，便于对比分析，本文仍沿用文献［3］中的熵权法确定各指标的权重，则W=(0.214，0.183，0.175，0.196，0.114，0.118)。

2.2.4 计算综合联系度，确定综合集对势

计算车辆野战维修装备编配方案的综合联系度为

由式(2)可求得整个方案的综合集对势，并根据综合集对势的大小结合表1 中的等级关系对方案进行排序，综合集对势shi(H)越大，方案整体评价越好。并且，还可根据单项指标的集对势对方案的单项指标进行比较，以便选出评价最好的指标，从而根据需要组合优化得出更好的新方案。

3 模型应用分析

把指标权重值和表2 中单项指标联系度代入式(3)，可计算得到车辆野战维修装备编配方案综合联系度;再运用式(2)可求得车辆野战维修装备编配方案的综合集对势;然后根据集对势shi(H)大小对各个待选方案进行排序，选出最优方案。计算结果见表3。

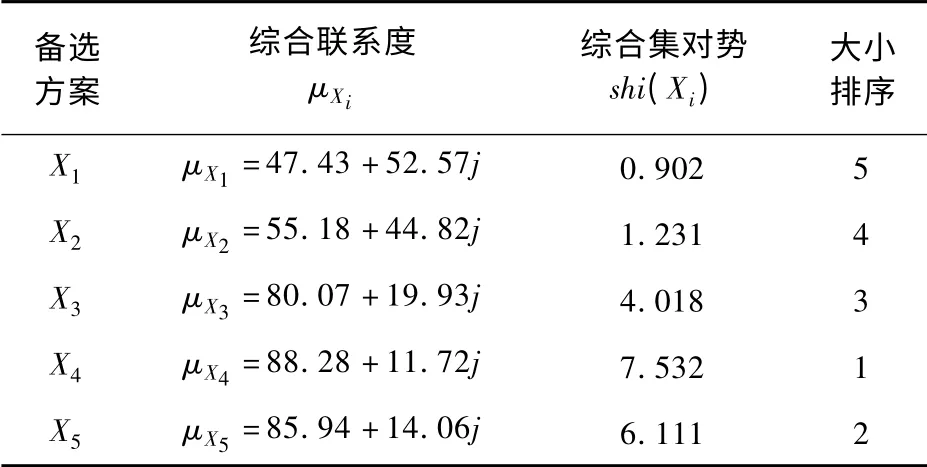
表3 综合联系度、集对势以及排序结果

根据表3 可知，车辆野战维修装备编配应用方案优劣排序依次为X4、X5、X3、X2、X1，X4方案为整体最优，可以优先被选用。

但是，通过计算表2 中各单项指标联系度的集对势不难发现，方案X5维修作业能力指标的集对势shi(μ51)=95/5 =19 ＞shi(μ41)=90/10 =9，技术性能先进性指标的集对势shi(μ56)=92/8 =11.5 ＞shi(μ46)=88/12 =7.33，方案X3种类配套性指标的集对势shi(μ34)=shi(μ44)=85/15 =5.67。也就是说，方案X5的维修作业能力和技术性能先进性2 项指标优于方案X4，可以认为是“局部最优”，方案X3的种类配套性指标与方案X4基本相当。因此，在方案实际应用过程中，可以根据实际需要以及综合考虑方案的实施条件，把各局部最优模块选取出来，重新组合生成一个新方案，从而达到真正最优的目标。

4 结 语

基于集对势理论的车辆野战维修装备编配方案优选模型，计算结果与文献［3］结果完全一致，说明模型比较可靠。但是，从模型构建与计算过程可以发现，本方法比文献［3］中的方法简便易算。重要的是，本方法能够进一步从微观分析各指标的优劣，从而为组合优化新方案提供了理论支撑。

借助于集对分析理论处理确定性与不确定性因素时辨证分析的优势，确保了评价决策的客观性，能够提高指挥决策的科学性。同时，为解决军事领域类似评价问题提供了一种新思路。由于车辆野战维修装备编配方案优选指标体系比较单一，只有一层指标，使利用集对势分析各指标优劣的价值没有完全显现出来。如果评价指标体系层级较多(3 层以上)，各层级中的指标权重又各不相同，就可以在利用综合集对势计算找出整体最优方案的基础上，采用逐级加权求集对势的方法找出局部最优的单项指标和层级指标模块，尔后组合优化得出最优方案。

［1］ 徐赤峰，赵劲松，张芳凌. 战时车辆野战维修装备编配方案优选研究［J］.装备学院学报，2013，24(2):131-133.

［2］ 赵劲松，康建设，张星辉，等.基于熵权-双基点法的战时野战维修装备编配方案优选研究［J］. 军械工程学院学报，2012，24(5):1-4.

［3］ 舒华，柴怡，赵劲松，等.基于熵权双基点法的车辆野战维修装备应用方案选优研究［J］. 军事交通学院学报，2011，13(9):33-36.

［4］ 赵克勤.集对分析及其初步应用［M］. 杭州:浙江科技出版社，2000:4-8，15-19，68-77.

［5］ 马亚龙，邵秋峰，孙明，等. 评估理论和方法及其军事应用［M］. 北京:国防工业出版社，2013:39-59.