双感应测井幅度差及“双轨”分析*
2014-12-24胡春桥谢伟彪殷秋丽刘迪仁
胡春桥 谢伟彪 殷秋丽 刘迪仁
(1.油气资源与勘探技术教育部重点实验室(长江大学) 湖北 武汉)
(2.长江大学地球物理与石油资源学院 湖北 武汉)
(3.冀东油田勘探开发研究院 河北 唐山)
0 引 言
在常规裸眼井测井中,双感应测井是很重要的测井方法。深、中感应测井曲线分别主要反应原状地层和侵入带的电阻率,它们结合能够很好的反应地层在径向上的电阻率的变化情况。理论上,在渗透性层段,由于泥浆侵入的存在,会使得侵入带电阻率不同于原状地层电阻率;在非渗透性层段,由于不存在泥浆侵入,侵入带电阻率与原状地层电阻率是相等的。基于这个原因,一般认为深、中感应测井曲线在渗透性层段会分离,即出现幅度差,而这两条曲线在非渗透性层段会重合。因此,根据幅度差就可以很好的识别渗透性层段和非渗透性层段,并且根据正、负幅度差异可以快速直观的识别油、水层段[1]。但是,测井工作者在实际测井资料中发现,有时候在非渗透性层段也会出现深、中感应测井曲线分离的情况,即所谓的“双轨”现象,这种现象给测井解释工作带来了一定的困难。
目前,关于“双轨”方面的研究主要是针对侧向测井的,针对感应测井的研究还比较少。1986 年赵良孝、补勇[2]研讨了在重泥浆钻井条件下地层中高角度缝形成双侧向“双轨”的原因。1999 年柯式镇、冯启宁等[3]对双侧向测井幅度差的影响因素进行了分析,并在此基础上分析了引起双侧向“双轨”的主要因素有仪器故障、仪器常数K 值变化和环境介质。
本文通过数值模拟的方法,对双感应测井幅度差的影响因素进行讨论,并在此基础上分析产生“双轨”现象的原因。
1 双感应测井正演计算
为了讨论深、中感应测井幅度差的影响因素,建立如图1 所示的典型的具有旋转对称性的三层介质地层模型[3]。其中,h 是目的层厚度,Rt是原状地层电阻率,Rs是围岩电阻率,Ri是侵入带电阻率,Rm是泥浆电阻率,di 是侵入深度,dm 是井眼半径。T1、T2、T3为深感应与中感应共用的发射线圈,R1、R2、R3为深感应接收线圈,r1~r5为中感应接收线圈。
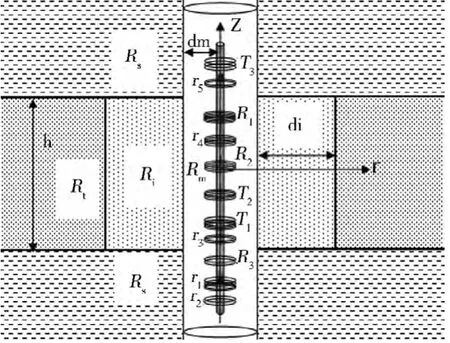
图1 地层模型
双感应测井仪器位于井眼中心,如图1 所示。根据Maxwell 方程组,电场→E 满足
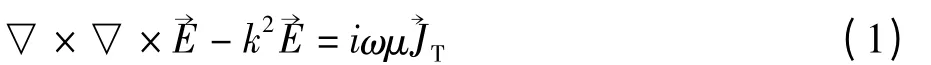
其中,k2=iωμσ(r,z),ω 是角频率,μ 是磁导率,→JT是发射线圈T 中的电流密度。在轴对称条件下,源在周围介质中产生的电场只有φ 方向分量[4]。因此,在柱坐标系下,由(1)式可得到在无源区域内,第S 层的电场满足如下关系[4]
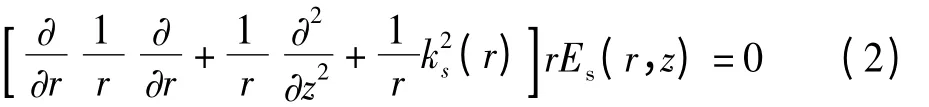
其中,k2S(r)=iωμσ(r)。基于分离变量法,将电场表示为[5、6]

将(3)式代入(2)式可以得到
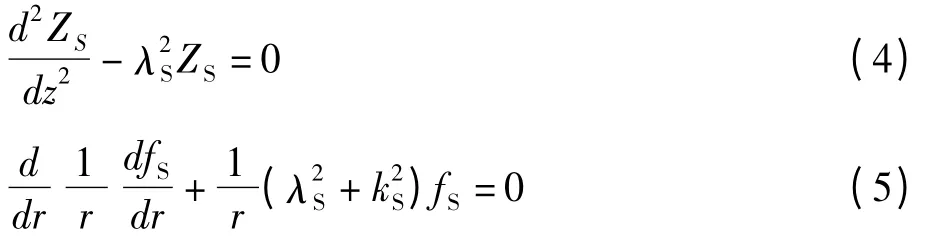
其中,λ2S是本征值。ZS(z)只与z 方向有关,可以得到解析解。fS(r)只与r 方向有关,求解(5)式等同于求使泛函数F(fS)达到极值时的fs(r)[5、6]

因此,可以得到fS(r)的数值解,再根据(3)式就可以得到每一层的电场,继而求得双感应测井的视电阻率。
在该地层模型下,以1503 双感应测井仪为例,忽略仪器自身影响,编程计算深、中感应测井响应在不同情况下的比值,用两者比值的变化来反应幅度差的变化情况。
2 双感应测井幅度差的影响因素
2.1 侵入带对双感应幅度差的影响分析
图2 给出的是有泥浆侵入(渗透层)时,深、中感应测井值的比值RILD/RILM在不同侵入带电阻率Ri情况下随侵入深度di 的变化曲线。其中,地层厚度h 为10m,井眼半径dm 为0. 1 m,原状地层电阻率Rt为100 Ω·m,泥浆电阻率Rm为2 Ω·m,围岩电阻率Rs为20Ω·m。
在图2 中,在泥浆低侵(Ri/Rt<1)情况下,由于中感应受泥浆侵入影响比深感应要大,使得中感应值相比深感应要小(RILD/RILM>1),测井曲线表现出正幅度差;随着侵入深度在一定范围内变大时会使得中感应的值进一步变小,因而RILD/RILM会在一定侵入深度内变大,当侵入深度继续增加到一定程度,侵入带也会对深感应产生较大影响,使得深感应的值有所下降,因而RILD/RILM又会随着di 的继续增大而减小,这样就出现了一个极大值点,此时测井曲线的正幅度差最大;当侵入深度再继续增加到一定程度(大于深感应的探测深度)后,泥浆侵入对两者的影响会相差不大,深、中感应测井曲线会趋于重合。
在泥浆高侵(Ri/Rt>1)情况下,由于侵入带电阻率高,使得中感应值相比深感应要大(RILD/RILM<1),测井曲线表现出负幅度差。随着侵入深度在一定范围内变大时会使得中感应的值进一步变大,因而RILD/RILM会在一定侵入深度内变小,当侵入深度继续增加到一定程度,深感应的值也会由于侵入带的影响而有所增加,因而RILD/RILM会随着di 的继续增大而增大,这样就出现了一个极小值点,此时测井曲线的负幅度差最大;当侵入深度再继续增加到一定程度后,泥浆侵入对两者的影响也会相差不大,深、中感应测井曲线也会趋于重合。
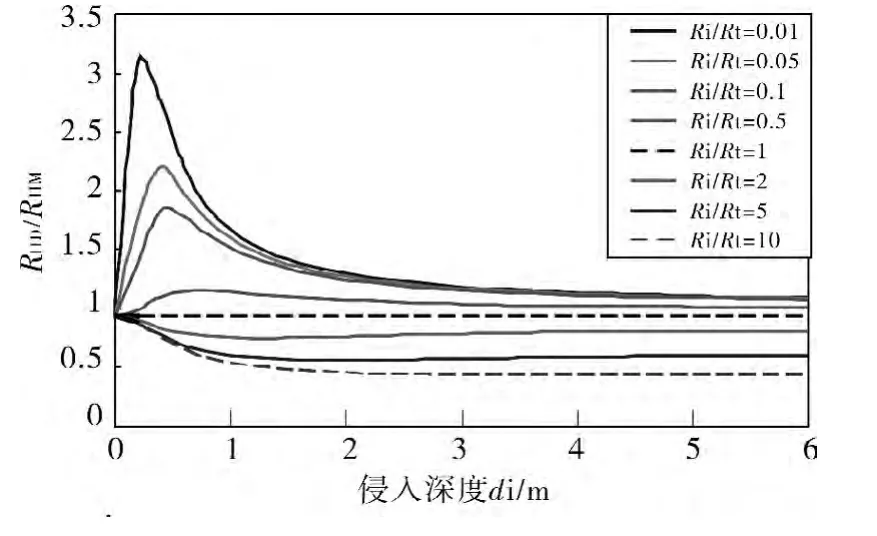
图2 不同Ri 情况下,di 对RILD/RILM的影响
图3 给出的也是有泥浆侵入时,RILD/RILM在不同侵入带电阻率Ri情况下随侵入深度di 的变化曲线。其中,地层厚度h=2 m,其他参数设置与图2 相同。从图中可以看出,图3 的变化趋势及出现幅度差的情况与图2 大致相同,但是在泥浆高侵时,RILD/RILM的变化曲线没有明显的极小值点;并且无论是在泥浆高侵时还是在低侵时,测井曲线都会显示出不同程度的幅度差。图3 与图2 之间的差异主要是由于地层厚度变薄时,双感应测井受较严重的围岩影响造成的。
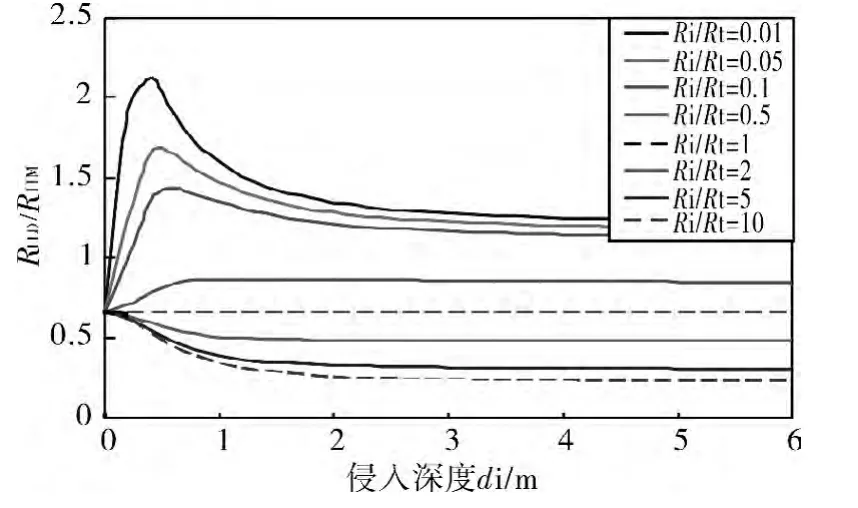
图3 不同Ri 情况下,di 对RILD/RILM的影响
图4 给出的是有泥浆侵入(渗透层)时,深、中感应测井值的比值RILD/RILM在不同侵入深度di 情况下随侵入带电阻率Ri的变化曲线。其中,参数设置与图2相同。从图中可以看出,当di=0(无侵入)时RILD/RILM趋近于1,深、中感应测井曲线是重合的;当di≠0(有侵入)时,由于中感应比深感应受侵入带影响大,在低阻侵入(Ri/Rt<1)时测井曲线会出现正幅度差,在高阻侵入(Ri/Rt>1)时会出现负幅度差;并且Ri与Rt的差别越小,深、中感应测井曲线之间的幅度差异越小。对于某一侵入深度,Ri/Rt>20 或Ri/Rt<0.01 时RILD/RILM基本上不再随Ri的变化而变化,此时幅度差主要受侵入深度的影响,而几乎不再受Ri的变化的影响。
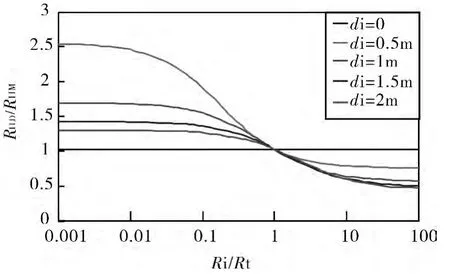
图4 不同di 情况下,Ri 对RILD/RILM的影响
由以上分析过程可以看出,侵入带电阻率和侵入深度都会对双感应测井的幅度差产生影响。一般情况下,低侵会出现正幅度差,侵入深度在0.5 m 左右时,幅度差最大;高侵会出现负幅度差。
2.2 围岩对双感应幅度差的影响分析
图5 给出的是在无侵入模型(非渗透层)下,深、中感应测井值的比值RILD/RILM在不同的地层厚度h 情况下随围岩电阻率Rs的变化曲线。其中,井眼半径dm为0.1 m,原状地层电阻率Rt、泥浆电阻率Rm以及侵入带电阻率Ri均为100 Ω·m。
从图中可以看出,当地层厚度较薄时,RILD/RILM随着Rs的增大先是变化比较平缓,接着随Rs的增大而增大,此时测井曲线一直存在负幅度差,这是由于深感应受围岩影响要比中感应大的原因,在低阻围岩(Rs<Rt)影响下使得深感应的值要比中感应的值小(RILD/RILM<1),所以会显示出负幅度差;随着Rs的继续增大,围岩电阻率逐渐接近并大于原状地层电阻率,使得深感应的值逐渐增大,当地层较薄(h =2 m)时表现出正幅度差,当地层较厚(h≥5 m)时,围岩对深感应影响会相对变弱RILD/RILM随着Rs的变化不是很明显,此时深、中感应测井曲线基本重合。
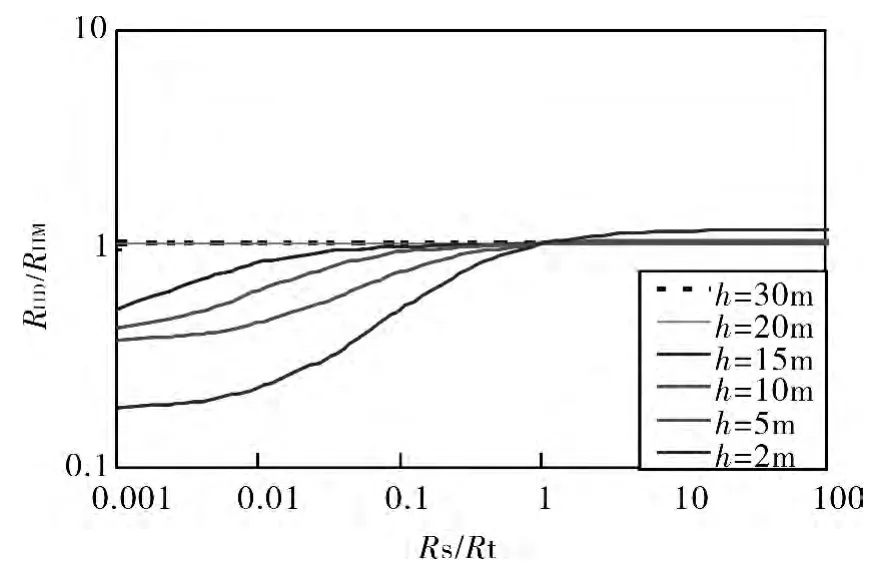
图5 不同h 情况下,Rs 对RILD/RILM的影响
图6 是在无侵入模型(非渗透层)下,深、中感应测井值的比值RILD/RILM在不同围岩电阻率Rs情况下随地层厚度h 的变化曲线。其中,地层参数设置与图5相同。
从图中可以看出RILD/RILM的变化曲线上有一个极值点,极值点的极性取决于Rs与Rt之间的大小关系。由于深感应受围岩影响比中感应要大,当Rs>Rt且地层厚度很薄时,高阻围岩使得深感应的值变大,随着厚度增加这种影响又会逐渐减弱,因而Rs/Rt>1 时RILD/RILM曲线上会出现极大值点,当h <10 m 时由于受高阻围岩影响使得RILD>RILM,测井曲线表现为正幅度差,当h >10m 时深、中感应几乎不受到围岩影响RILD/RILM趋近于1,测井曲线重合;当Rs<Rt且厚度很薄时,低阻围岩使得深感应的值变小,随着厚度增加这种影响会逐渐减弱,因而会出现极小值点,当h <15m 时由于受低阻围岩影响使得RILD<RILM,测井曲线表现为负幅度差,当h >15m 时深、中感应几乎不受到围岩影响RILD/RILM趋近于1,深、中感应测井曲线也会趋于重合。
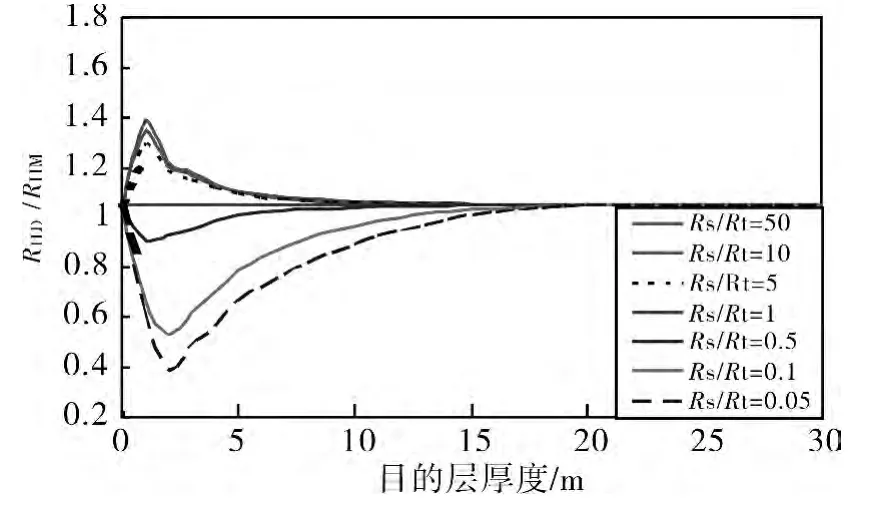
图6 不同Rs 情况下,h 对RILD/RILM的影响
由图5、图6 的分析可知,即使是非渗透层,由于目的层厚度和围岩的影响,也会使双感应测井曲线出现幅度差,也就是“双轨”现象。当地层厚度较薄时,高阻围岩会使双感应测井表现出正幅度差,低阻围岩时会出现负幅度差,而且围岩电阻率与目的层电阻率差异越大,幅度差越明显;当地层厚度较厚时,双感应测井曲线基本重合。
2.3 井眼泥浆对双感应幅度差的影响分析
图7 给出的是在无侵入模型(非渗透层)下,深、中感应测井值的比值RILD/RILM在不同泥浆电阻率Rm情况下随井眼半径dm 的变化曲线。其中,目的层厚度h为5 m,原状地层电阻率Rt、围岩电阻率Rs以及侵入带电阻率Ri均为100 Ω·m。
从图中可以看出,在泥浆电阻率较低(Rm/Rt<1)且井眼半径大于仪器半径(0.05 m)时,测井曲线会出现正幅度差,这是由于中感应受井眼影响比深感应大的原因,低阻钻井液会使中感应的值比深感应的值小(RILD/RILM>1),因此测井曲线会显示出正幅度差;在泥浆电阻率较高(Rm/Rt>1)时RILD/RILM基本上不会随着dm 的变化而变化,幅度差不明显,测井曲线基本上趋于重合。
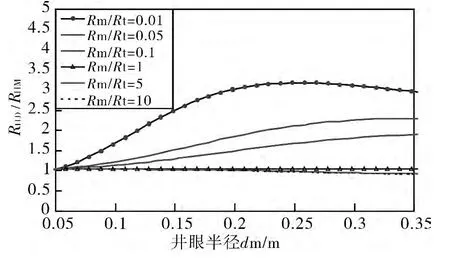
图7 不同Rm 情况下,dm 对RILD/RILM的影响
图8 给出的是在无侵入模型(非渗透层)下,深、中感应测井值的比值RILD/RILM在不同的井眼半径dm 情况下随泥浆电阻率Rm的变化曲线。其中,地层参数设置与图7 相同。从图中可以看出,当泥浆电阻率较低(Rm/Rt<1)时,测井曲线会出现明显的正幅度差,并且当Rm逐渐接近Rt时,幅度差在减小,这是由于Rm在逐渐变大的过程中对中感应的影响在逐渐减小的原因;在Rm/Rt>1 时,幅度差不明显,测井曲线基本保持重合,这与图7 反应的结果是一致的。

图8 在不同的dm 情况下,Rm 对RILD/RILM的影响
由图7、图8 的分析可知,即使是非渗透层,由于井眼和泥浆的影响,也会使双感应测井曲线出现幅度差,即“双轨”。当井眼存在扩径,泥浆电阻率较低的情况下会出现正幅度差,而且泥浆电阻率越低,井眼半径越大,幅度差越明显。
3 出现“双轨”现象的原因分析及处理
由以上分析可以发现,很多情况下都会造成双感应测井曲线的幅度差,不仅在渗透性层段会出现,在非渗透性层段(无侵入模型)也会出现,并且既有正幅度差,也有负幅度差。在实际测井过程中,由于偶尔的仪器故障有可能导致“双轨”现象[3]。从对双感应测井幅度差的影响因素的分析来看,由于仪器自身的探测特性,各地层环境因素对深、中感应的影响也不一样,因此即使是在非渗透层,复杂的地层环境因素会造成深、中感应在同一深度点所测值不一样,也就造成了“双轨”现象。
为了消除地层环境影响造成的“双轨”,可以利用传统的资料处理手段,比如围岩校正、井眼校正和反演[7、8]等方法来处理测井资料,从而获得更加准确的地层信息。
4 结 论
通过数值模拟的方法,分析了各因素对双感应测井幅度差的影响。根据以上分析可以总结出以下几点结论:
(1)由分析过程可以发现,围岩、侵入、井眼等复杂环境因素都会对幅度差产生影响。一般情况下,低侵会出现正幅度差,高侵会出现负幅度差;当地层较薄时,高阻围岩会产生正幅度差,低阻围岩会产生负幅度差,围岩与目的层电阻率差异越大,幅度差越明显;当井眼扩径,泥浆电阻率较低时会产生正幅度差,且泥浆电阻率越低,井眼半径越大,幅度差越明显。
(2)不仅在渗透性层段会产生深、中感应测井曲线分离现象,在非渗透性层段也会产生,也就是“双轨”。仪器故障和复杂的地层环境因素都有可能导致“双轨”。对于非渗透性层段,当目的层较薄,井眼扩径严重,泥浆电阻率非常低,围岩与目的层电阻率相差较大等,都有可能造成“双轨”。
(3)测井响应是地层中诸多因素的综合体现,不同的地层条件和井眼环境会产生不同的幅度差。利用双感应测井幅度差来评判地层特性时,需要综合考虑各方面因素变化。
[1]邓少贵,范宜仁,谢关宝,等. 泥浆侵入地层双感应测井曲线正负差异特性分析[J].测井技术,2004,28(6)
[2]赵良孝,补 勇.对双侧向测井“双轨”现象的认识和评价[J].天然气工业,1986,6(3)
[3]柯式镇,冯启宁,孙艳茹,等. 双侧向测井幅度差的影响因素与“双轨”现象[J].测井技术,1999,23(2)
[4]张庚骥,汪涵明,汪功礼. 成层介质中交流电测井响应[J].地球物理学报,1995,38(6)
[5]谭茂金,张庚骥,运华云,等. 非轴对称条件下用三维模式匹配法计算电阻率测井响应[J]. 地球物理学报,2007,50(3)
[6]谭茂金,张庚骥,谢关宝. 电阻率测井三维模式匹配法中的平面数值分析[J].中国石油大学学报(自然科学版),2007,30(2)
[7]汪宏年,陶宏根,王桂萍,等. 双感应测井资料的快速近似迭代反演[J].地球物理学报,2007,50(5)
[8]刘振华,成志刚,仵 杰. 高分辨率双侧向与双感应测井联合反演[J].西安石油大学学报(自然科学版),2010,25(6)
