MWD 随钻测井仪减振器结构设计与研究
2014-12-24闫麦奎卫一多赵常青颖梁羽佳王涯菲
闫麦奎 刘 枭、2 卫一多 赵常青、3 马 颖梁羽佳 徐 韧 王涯菲 奥 云
(1.中国石油集团测井有限公司随钻测井中心 陕西 西安)
(2.西安石油大学 陕西 西安)(3.西安理工大学 陕西 西安)
0 引 言
MWD 无线随钻测井仪作为随钻测井仪器的一个重要组成部分,在随钻测井仪器中发挥着不可替代的作用。MWD 随钻测井仪的主要功能包括测量井斜角、方位角、工具面角及辅助参数,如温度等[1],并将测量到的地层数据及时地通过无线传输的方式传递给测井的地面系统。地面系统通过相应的算法处理成相对应的地层物理信息,指导实时钻井作业和后期的油气开发。由于随钻测井仪器在测井过程中受钻铤振动、泥浆冲刷等影响,工作环境十分恶劣,而MWD 随钻测井仪作为连接转换短节,其可靠性直接决定着整套随钻测井仪的可靠性。随钻测井与传统的电缆测井不同,随钻测井仪器将测井探测仪器安装在钻铤上,随着钻杆在钻井的过程中实现测井。其测井的井况环境十分恶劣,相关的钻井实践和测量资料表明,随钻测井仪器在井下受到的振动量级在15 g ~20 g(g 为重力加速度,g=9.8 m/s2)之间,瞬间的冲击可达到50 g 左右,甚至更大的量级。而目前所用的MWD 随钻测井仪连接方式为刚性连接,此连接方式的优点是结构简单、连接方便;但是处在强振的井况环境下,极易受到钻柱振动和冲击的影响而造成MWD 测井仪器的损坏,从而降低MWD 仪器的测井可靠性。因此,从产品的可靠性、经济效益等方面考虑,急需研制一种新型的可有效减小和吸收钻杆冲击、振动,结构简单,可靠性高的随钻测井仪减振器来达到减小振动、吸收冲击的目的,从而提高MWD 测井仪器的可靠性。
1 随钻测井仪器减振器的设计
1.1 问题分析
随着MWD 仪器在国际、国内市场上的推广应用,仪器因振动与冲击而造成损坏的情况占很大一部分比例。为了更好地优化减振器的结构,对仪器的振动原因分析如下。
图1 为MWD 仪器结构连接示意图。沿圆周方向安装有翼型扶正器及O 型橡胶圈用来减小圆周方向的振动。由于在钻井施工过程中沿着仪器圆周方向的振动较轴线方向的振动小很多,所以沿圆周方向的振动不是仪器损坏的主要原因[2]。

图1 MWD 仪器结构连接示意图
在沿仪器轴线方向,MWD 仪器和翼型扶正器为刚性连接,使得钻井过程中钻头冲击振动直接传递到MWD 仪器上,由于此种连接没有缓冲减振的结构,从而导致MWD 仪器的损坏;另外,这种连接方式使得仪器长时间处于交替载荷冲击下,易导致螺纹松扣,最终损坏仪器。为使问题得到较好的解决,应用振动理论[3]对问题进行理论分析,为仪器优化改进提供指导和方向。
1.2 理论分析
图1 为MWD 仪器结构连接示意图,应用线性振动理论的集中质量法,将原有的结构简化为单自由度强迫振动的力学模型。简化建立在以下3 个假设之上:
①由于井下振动的激励力较为复杂,简化为一种简谐激励f0sinωt;
②仪器质量抽象为一个质量块m;
③弹簧、及摩擦力的阻尼忽略,故认为阻尼c=0。
图2 为仪器的振动力学简化模型。图2(a)为简化模型第一步,将刚性连接简化为弹簧,K1 和K2 分别为弹簧的弹性系数;由其等效模型可知弹簧K1 和弹簧K2 为并联,如图2(b)所示;系统等效的弹性系数为K=K1 +K2,如图2(c)。

图2 仪器的振动力学简化模型
单自由度系统无阻尼受迫振动的微分方程为:

当ω≠ωn时,微分方程(1)的解为:

当ω=ωn时,微分方程(1)的解为:


根据公式(3),当初始条件为u(t)= 0;u˙(t)=1 m/s时,通过Matlab 编程仿真,结果如图3 所示。

图3 无阻尼共振响应曲线
从图3 的无阻尼共振响应曲线可以看出,在无阻尼的情况下,当外界激励的频率与仪器的固有频率相同时,即会引发仪器的共振,形成能量的累积,以振动的形式释放出来,对仪器造成损坏。为消除系统的共振现象,吸收系统多余的振动能量,就需要更改仪器的结构,加入阻尼来吸收多余能量,达到减振的目的。为此,建立如图4 所示的有阻尼的单自由度受迫振动力学模型,探讨阻尼结构对系统振动响应的影响。
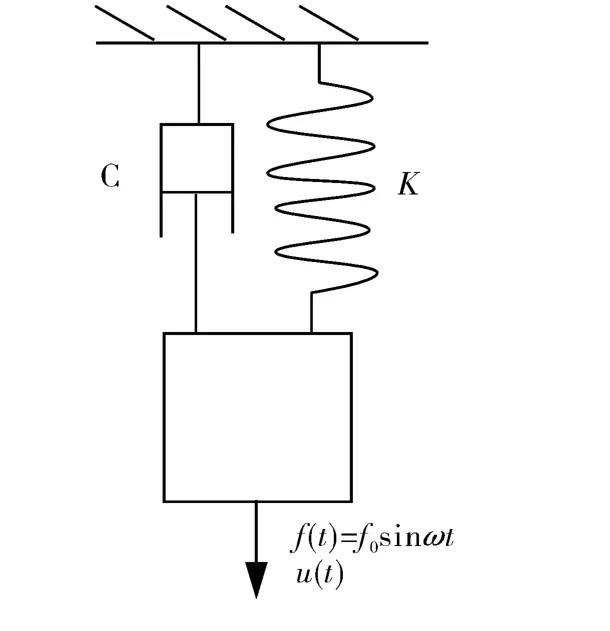
图4 有阻尼的单自由度受迫振动力学模型
单自由度有阻尼受迫振动系统的微分方程为:

微分方程(4)的解为:

式(5)中,e 为自然常数;c 为系统的阻尼;ψd为系统相位;Bd为微分方程解的常数,由系统的初始条件和约束条件决定;ζ 为相对阻尼系数。
对微分方程(4)的解(5)在初始条件u(t)=0.05 m,u˙(t)=1 m/s,进行Matlab 仿真,得出有阻尼的单自由度系统受迫振动的响应曲线,如图5 所示。
从图5 有阻尼的单自由度系统受迫振动的响应曲线可以看出,对于单自由度有阻尼系统的受迫振动而言,在外界周期性激励的作用下,尽管系统存在阻尼,但系统的振幅响应仍为周期性的,且振动幅度不会随着时间的推移而衰减。这说明在有外界能量持续输入的情况下,尽管系统存在阻尼,但不足以抵消外界输入的能量,系统的振动还会持续下去。

图5 有阻尼的单自由度系统受迫振动的响应曲线
以上的分析计算都是在振动系统的结构和参数确定的情况下进行的。为了使分析更具有普遍的意义,消除单位的影响,在这里引入无量纲参数[3]进行分析:
当系统在低频段时,振动参数为:λ <<1,βd≈1;
当系统在高频段时,振动参数为:λ >>1,βd≈0;
当系统在共振段时,振动参数为:
λ=1,βd=1/(2ζ);
从图6 单自由度振动系统的阻尼幅频特性可以看出,单自由度有阻尼受迫振动的阻尼在共振区,即ζ =0.1,λ =1 时,系统振幅的放大因子βd=5;而当ξ =0.01,λ=1 时,系统的振幅的放大因βd→∞,对减小系统的响应振幅有显著作用;在远离共振区,即ξ =0.707,λ=2 时,系统振幅的放大因子βd≈0.3,阻尼对减小系统的响应振幅的作用不大。共振时弹性力与惯性力相平衡,系统的响应由阻尼力与激振力之间的平衡关系确定,系统基本呈阻尼特性。即在共振区域,系统的响应幅值的大小由阻尼力与激振力之间的差值决定,要想获得较小的响应幅值,在外界激励力不变的情况下,就要加大系统的阻尼,在共振区域来抵消激振力对系统振幅响应的贡献。
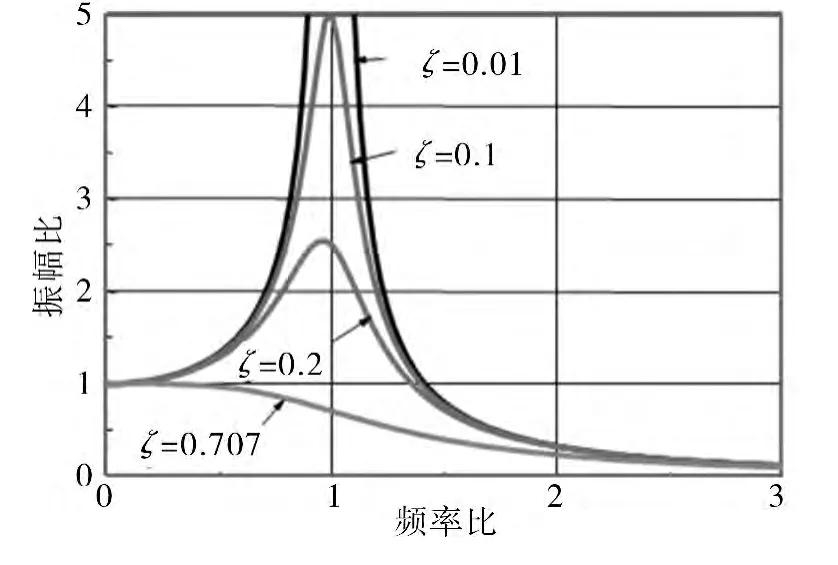
图6 单自由度振动系统的阻尼幅频特性
1.3 Simulink 仿真结果及分析
Simulink 基于Matlab 的仿真平台,可以调用Matlab集成的库函数,而且可以方便地修改仿真参数,考察各设计参数对系统振动响应的影响,为系统振动的优化设计提供很好的工具。利用Matlab 的Simulink 仿真平台对单自由度系统在周期性激励作用下无阻尼与有阻尼两种情况进行仿真,来考察系统参数对系统响应的影响。

无阻尼时:
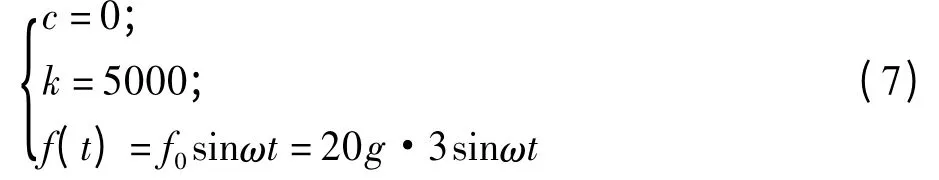
有阻尼时:
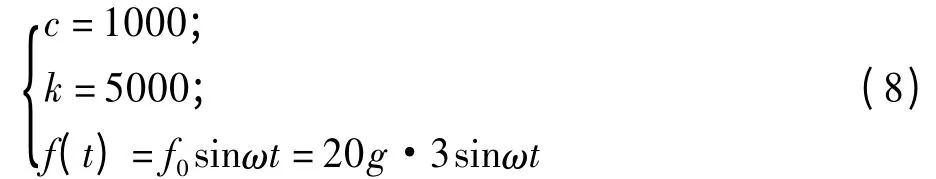
在初始条件u(t)=0.01 m,u˙(t)=1 m/s 时对方程(6)在无阻尼和有阻尼的情况下,考察系统的振幅和振动速度随时间的响应,响应曲线分别如图7、图8 所示。
从图7 无阻尼振幅响应曲线与有阻尼振幅响应曲线对比可以看出,加入阻尼后最大振幅由原来的0.05 m减小到0.013 m;从图8 无阻尼振动速度响应曲线与有阻尼振动速度响应曲线对比可以看出,加入阻尼后最大速度由原来的0.8 m/s 减小到0.06 m/s。仿真结果说明:加入阻尼后,系统的振动得到很好的抑制,可以有效地保护仪器。按照工程设计要求[3],在5个周期内阻尼的作用应该将最大振幅0. 05 m 降到0.013 m,可以得出:
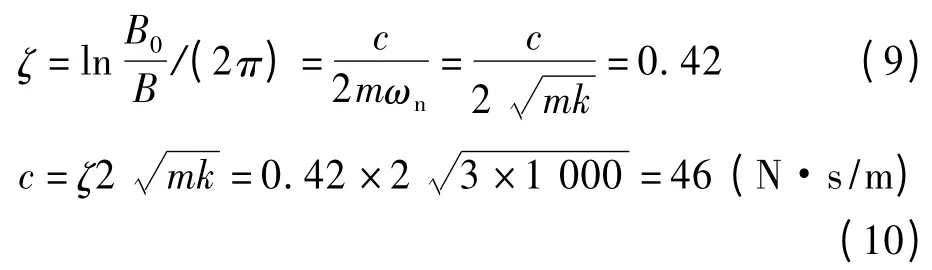
1.4 减振器的结构改进
根据理论分析的结论以及MWD 测井仪实际的使用条件,对减振器的结构进行改进。
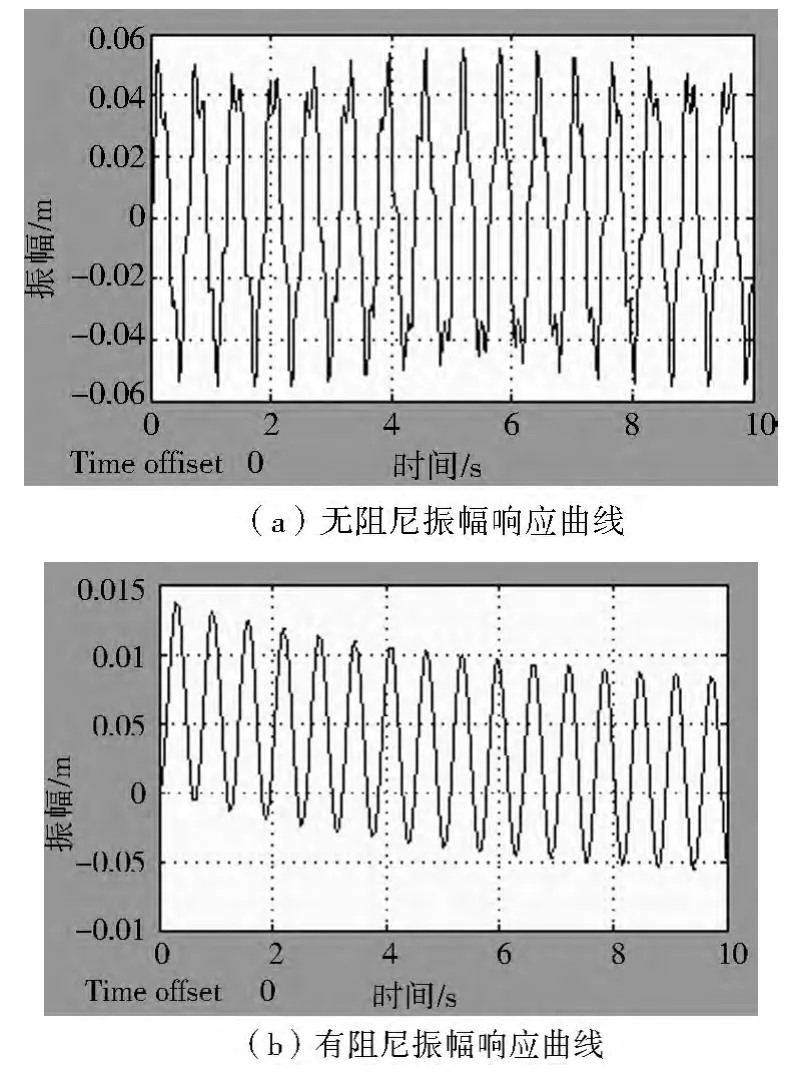
图7 系统的振幅响应曲线

图8 系统的速度响应曲线
1.4.1 阻尼选型
由于随钻石油测井仪器长时间工作在高温、高压和强的振动、冲击和泥浆腐蚀的井况下,工作环境十分恶劣。因此选用的阻尼材料需要耐高温、耐高压、抗腐蚀;具有良好的疲劳强度、良好的减振效果;具有粘性阻尼特性。
经综合考虑,阻尼材料选用氟橡胶。
1.4.2 阻尼结构设计
根据仪器安装需求,要求减振器既可以减振又要有一定的连接刚度,改进设计采用了接触面积大的双花键结构。图9 所示为改进设计的阻尼器结构。主要由定位销、外壳、氟橡胶、内壳组成。金属圆柱形的内、外壳主体内、外采用双花键结构,双花键结构增大了减振的阻尼橡胶材料的接触面积,满足了减振器具有一定连接刚度的要求,而且便于加工与拆装。减振材料选用氟橡胶夹在内、外壳体之间,可有效地缓冲系统的振动,吸收系统的冲击。改进的结构设计满足了随钻石油测井仪器可靠性高、操作简便的要求。
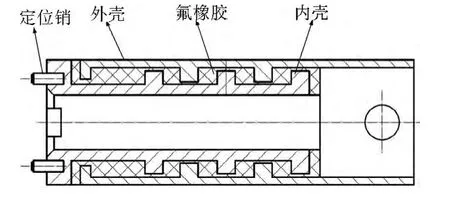
图9 改进设计后的阻尼器结构
1.4.3 结果分析
对改进设计后减振器结构进行仿真计算,改进设计后仪器的冲击稳定区域如图10 所示:双花键的氟橡胶减振器结构在仪器的外界振动强度为10 g ~30 g 的冲击力作用下,系统的振幅响应具有较好的稳定性和缓冲能力。而随钻测井仪器井下的振动强度范围大都分布在10 g ~20 g 之间。而在大于40 g 的冲击下,系统则处于不稳定的区域。由此可以看出,改进设计后减振器有效地减小了仪器的振动与冲击,提高了仪器的可靠性,达到了较好的改进目的。
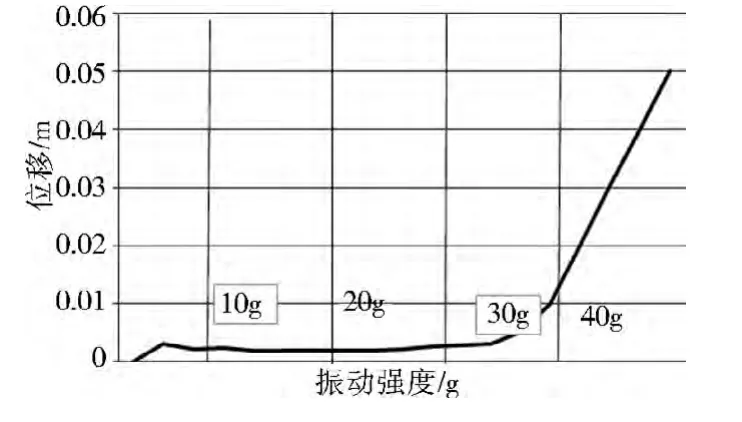
图10 改进设计后仪器的冲击稳定区域
2 结 论
1.建立了MWD 井下仪器的振动模型,在此基础上设计了适用于复杂井况的MWD 减振器;
2.降低了MWD 仪器因井下振动造成的损坏几率,提高了MWD 仪器应对复杂井况的能力,加大对深井开发的支持力度;
3.新型的结构振动减幅达80%,冲击力减幅达97%,有效地减小了振动对仪器的损害,基本达到了优化与改进的目的;
4.新型减振器结构简单、成本低、适用性高,性能好,可广泛地应用于随钻测井仪器。
[1]陈庭根,管志川,刘希圣. 钻井工程理论与技术[M]. 东营:石油大学出版社,1997
[2]陈理中,邹永言,蒋鼎铎,译. 美国钻井工程[M]. 北京:石油大学出版社,1974
[3]倪振华.振动力学[M].西安:西安交通大学出版社,1986
