特高含水期油田注水层段划分新方法

(中石油大庆油田有限责任公司勘探开发研究院，黑龙江 大庆 163712)

分层注水是缓解多层砂岩油田层间矛盾的有效途径。在油田开发初期，考虑水井单层厚度、渗透率及射开小层数，将渗透率相近的小层组合为一个注水层段，以达到注水层段内各小层均匀驱替的目的[1～3]，但是随着油田进入特高含水期以后，各小层含水率差异较大，渗流阻力大小不再只由静态因素(渗透率、有效厚度等)决定，相同渗透率小层在含水率不同时，渗流阻力也会存在较大差异，层段内各小层能否实现均匀推进，受油水井动静态因素共同影响[4～7]。为此，依据油水两相流达西公式，分析渗流阻力的影响因素，定量计算水井小层渗流阻力大小及层段组合的界限，将注水层段划分思路从近渗组合转变为近阻组合，以有效缓解特高含水期油田层间矛盾。

1 常规分层注水井层段组合方法及存在问题

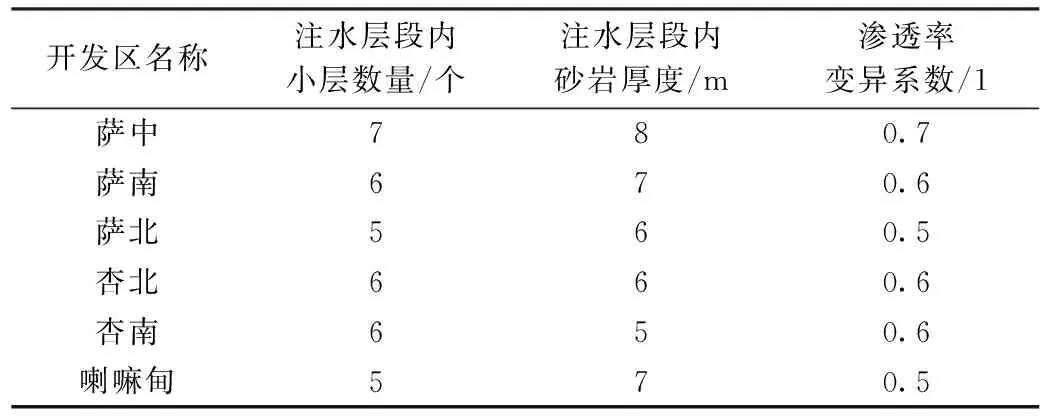
表1 大庆长垣油田6个开发区细分注水层段量化标准

大庆油田经过60多年的开发，经历了3次大的井网加密和层系细分调整，目前包括9个油层组，41个砂岩组，136个小层，小层有效厚度从0.2m到十几米，渗透率从0.01D到5D。为有效缓解层间矛盾，2010年大庆油田加大细分注水技术攻关力度，按照层段内砂岩吸水厚度比例达到80%以上目标要求，分别制定了6个开发区的注水井层段量化标准，具体见表1。

层段组合思路是满足层段内储量及吸水动用的需要，进行相近渗透率小层的组合，考虑的因素主要是水井静态指标，包括射开小层数量、射开砂岩厚度及小层渗透率变异系数[8～10]。然而随着油田进入特高含水期后，注入水在小层上的推进速度除了受井间地质参数变化、油水井距、油水井点射开厚度、渗透率及连通井数等静态因素影响外，还与小层含水率(fw)关系较大：含水率增加，油相相对渗透率(Kro)下降，水相相对渗透率(Krw)上升，水油相对渗透率比值急剧上升(见图1)，注入水推进速度变快。

图1 水相与油相相对渗透率比值随含水率的变化曲线

特高含水期各小层渗透率差异，已不能代表各小层渗流能力的差异。因此，注水层段的划分应该考虑影响渗流阻力大小的动静态因素，将渗流阻力相近的小层进行组合。

2 影响渗流阻力的因素分析

根据达西定律推得渗流阻力公式如下：

(1)

式中：R为渗流阻力，mPa·s/(D·m)；K为渗透率，D；A为渗流面积，m2；L为注采井距，m；μo为油相黏度，mPa·s；μw为水相黏度，mPa·s。

将流经单位截面积、单位长度的渗流阻力的大小定义为阻力系数Rd，则渗流阻力公式为：

(2)

由式(2)可知，渗流阻力R与渗流面积A成反比，与阻力系数Rd及注采井距L成正比。阻力系数Rd随着含水率的变化而变化，可以利用相对渗透率曲线及分流方程计算不同含水率时阻力系数的大小,结果见图2和图3。

注：Sw为含水饱和度。 图2 不同渗透率岩心的相渗曲线 图3 不同渗透率岩心的阻力系数随含水率的变化曲线

从计算结果可以看出，在低含水阶段，阻力系数大小主要受渗透率大小控制，随含水率变化不明显；随着含水率的增加，在相同渗透率情况下，阻力系数逐渐减小，渗透率越低，渗流阻力减小的值越大；含水率大于90%后，阻力系数随含水率变化尤为明显。

对于实际井网来讲，注水井某一小层的渗流阻力还要受油水井间的物性参数变化、连通类型及连通方向数等影响。

3 小层平面渗流阻力计算

以水井为中心，先计算小层上油水井间渗流阻力，再按照水电相似原理[11～13]，计算小层平面渗流阻力。

3.1 平面单方向上渗流阻力计算

主流线方向上注水推进最快，阻力最小，油水井间渗流阻力近似为主流线上的渗流阻力。主流线上任一点的流动阻力R(x)表示如下：

(3)

式中：x为油水井连线上任意一点距水井的距离,m；K(x)为x处的渗透率,mD；h(x)为x处的有效厚度,m。

注水井单层单个注采方向上的渗流阻力可采用积分计算：

(4)

式中：Ri为第i个注采方向的渗流阻力,mPa·s/(D·m)；rw为水井半径,m；d为注采井距,m。

R(x)表达式中所涉及到的参数很难找到与距水井距离x的解析关系式，式(4)采用数值离散求解，根据数值模拟结果计算油水井间主流线上每个网格的渗流阻力和即可得到Ri。

油水井点网格的K和h根据测井解释结果取值，暂不考虑长期注水引起的渗透率变化；井间网格的K和h根据精细地质模型中的网格地质参数取值；每个网格采用的相渗曲线根据数值模拟中的相渗曲线分区情况确定，不同油层组、不同微相采用不同相渗曲线；网格的油水两相相对渗透率可以利用数值模拟计算的剩余油饱和度，并结合网格处的相渗曲线进行计算；流体黏度考虑为常数。

3.2 小层平面渗流阻力计算

注水井单层上考虑多个注采方向，假设水井在某一沉积单元上周围有n口连通的油井，则第i口油井方向上的综合渗流阻力为Ri，依据水电相似原理，则平面上相当于有n个电阻并联，小层p的渗流阻力为：

(5)

4 注水井层段调整方法

层段调整的总体思路是在满足工艺条件的前提下，考虑所有的层段组合可能，以单井各层段内平均渗流阻力差异最小化为目标，确定最优的层段划分方案。

4.1 层段内渗流阻力差异表征参数筛选

一般用级差和变异系数表示数据内部差异及离散程度：级差代表最大值与最小值之间的差异，变异系数更能反映数据整体的均衡性[14]。设计5层纵向非均质理想模型，在其他参数均相同的情况下，只改变各层渗透率大小，结果见表2。计算结果显示,在渗流阻力级差保持为15不变的情况下，采收率随渗流阻力变异系数增加而降低，采收率随渗流阻力变异系数的变化更为敏感。

表2 渗流阻力差异表征参数筛选方案表

另外，级差易受极值影响产生异常值，因此这里采用变异系数表征层段内各小层渗流阻力差异。水井层段调整的目标就是要使单井平均层段渗流阻力变异系数最小化。

4.2 注水井层段调整步骤

1)根据目前工艺条件下的隔层厚度下限进行初步层段划分。考虑封隔器长度，层段间隔层厚度应不低于目前分层工艺下的隔层厚度下限，以保证封隔器有足够的长度空间分割上下油层，按照隔层约束条件，进行初步的小层段划分，共计划分为m段。

2)根据封隔器之间的间隔长度、单井最高的层段数及层段内最小有效厚度要求将初步划分的m段进行组合。①考虑测试工艺要求，封隔器之间的间隔长度不低于目前工艺条件下的下限，以保证水嘴之间有足够的测试距离；②单井层段数不超过目前工艺条件下的上限，以保证在作业时能够正常起下管柱；③考虑层段的吸水能力，层段内需要有足够的有效厚度，以保证层段最小注水量及测试精度的要求。

图4 注水井层段调整流程图

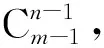
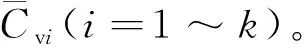
以上所涉及的工艺参数界限可能会根据不同油田、不同工艺技术的变化略作调整。整个计算过程可利用计算机程序实现自动化，流程图如图4所示。

5 实际应用

统计Z区块380口水井1651个注水层段内渗透率变异系数和渗流阻力变异系数分布比例，结果见图5。虽然大部分层段内渗透率变异系数较低，但是仍有一部分层段内的渗流阻力变异系数较大，可作为下一步进行层段细分、重组的重点。

图5 Z区块注水层段内渗透率及渗流阻力变异系数分布比例

该区块按照目前的分层工艺条件，给定最小隔层厚度1.2m，封隔器之间间隔长度下限7m，单井最多可分的层段数7个，层段内有效厚度下限2m。以S29井为例，该井原先有4个层段，按照有效厚度加权计算，各层段内渗透率变异系数均小于0.6，但是渗流阻力变异系数均在0.7以上，层段优化后层段数变为6个(见图6)，平均单井层段渗流阻力系数0.62，有5个层段的渗流阻力变异系数均在0.7以内，层段内渗流阻力差异明显下降。

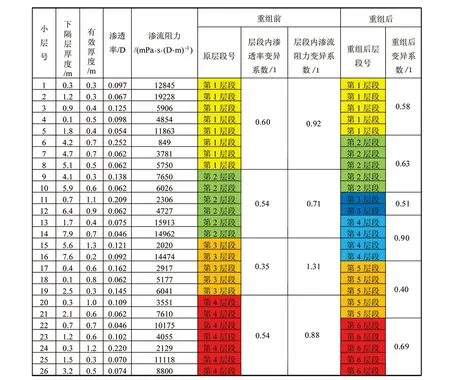
图6 S29层段重组情况

对该井实施细分重组后，井组内平均单井初期日增油0.3t。按照该方法在Z区块实施细分重组井共计10口，在油井平均含水率96%的情况下，平均单井初期日增油达0.2t。

6 结论

1)随着含水率的增加，渗流阻力逐渐减小；渗透率越低，渗流阻力减小的值越大；含水率在大于90%后，阻力系数随含水率变化尤为明显。油田进入特高含水期后，注水层段划分思路应从近渗组合转变为近阻组合。

2)井间渗流阻力计算所需要的参数依靠地质模型及数值模拟获取，精细地质模型及高精度数值模拟结果是保证渗流阻力计算结果准确性的基础。

3)注水井层段调整以目前分层工艺限制作为约束条件，以单井平均层段渗流阻力变异系数最小化为目标，可实现计算机自动化。

4)按照渗流阻力进行实际区块的层段调整取得了较好的效果，在区块综合含水率超过96%的情况下，单井日增油0.2t。